数据结构-图的生成树问题

一、无向图的连通分量和生成树

若图是连通的或强连通的，则从图中某一个顶点出发可以访问到图中所有顶点；
若图是非连通的或非强连通图，则需从图中多个顶点出发搜索访问。而每一次从一个新的起始点出发进行搜索过程中得到的顶点访问序列恰为每个连通分量中的顶点集。

1、生成树

深度优先搜索遍历算法及广度优先搜索遍历算法中遍历图过程中历经边的集合和顶点集合一起构成连通图的极小连通子图。它是连通图的一颗生成树。
生成树：是一个极小连通子图，它含有图中全部n个顶点，但只有n-1条边。
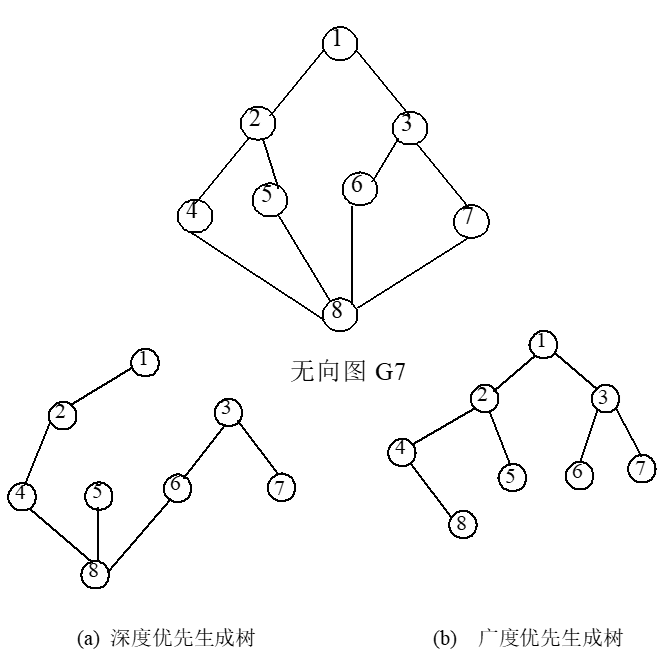
由深度优先搜索遍历得到的生成树，称为深度优先生成树，由广度优先搜索遍历得到的生成树，称为广度优先生成树。图中无向图G7的两种生成树见 图(a)、(b)。

2．生成森林

若一个图是非连通图或非强连通图，但有若干个连通分量或若干个强连通分量，则通过深度优先搜索遍历或广度优先搜索遍历，不可以得到生成树，但可以得到生成森林，且若非连通图有 n 个顶点，m 个连通分量或强连通分量，则可以遍历得到m棵生成树，合起来为生成森林，森林中包含n-m条树边。
生成森林可以利用非连通图的深度优先搜索遍历或非连通图的广度优先搜索遍历算法得到。

3．最小生成树

在一般情况下，图中的每条边若给定了权，这时，我们所关心的不是生成树，而是生成树中边上权值之和。若生成树中每条边上权值之和达到最小，称为最小生成树。

二、求最小生成树

首先明确：

• 使用不同的遍历图的方法，可以得到不同的生成树；从不同的顶点出发，也可能得到不同的生成树。
• 按照生成树的定义，n 个顶点的连通网络的生成树有 n 个顶点、n-1 条边。
  目标：
  在网络的多个生成树中，寻找一个各边权值之和最小的生成树。
  构造最小生成树的准则
• 必须只使用该网络中的边来构造最小生成树；
• 必须使用且仅使用n-1条边来联结网络中的n个顶点；
• 不能使用产生回路的边。

1. 克鲁斯卡尔算法基本思想

克鲁斯卡尔算法的基本思想是：将图中所有边按权值递增顺序排列，依次选定取权值较小的边，但要求后面选取的边不能与前面选取的边构成回路，若构成回路，则放弃该条边，再去选后面权值较大的边，n个顶点的图中，选够n-1条边即可。

#定义
typedef struct  Edge				//定义边集数组元素，v1,v2存顶点，weight存权重。
{
    int v1;
    int v2;
    int weight;
}Edge;

typedef struct ALGraph		//定义图的结构，peak存顶点的数量，edge存边的数量
{											//指针p作为边集数组，指针m为作为顶点数组
    int peak;
    int edge;
    Edge *p;
    int *m;
}ALGraph;
#创建图
void CreatALGraph(ALGraph *G)
{
    int i,j;
    printf("输入图的顶点数量和边的数量：");
    scanf("%d %d",&G->peak,&G->edge);
    G->p=(Edge *)malloc(sizeof(Edge)*(G->edge+1));
    G->m=(int *)malloc(sizeof(int)*G->peak);
    for(i=0;ipeak;i++)
    {
          printf("请输入输入顶点：");
          scanf("%d",&G->m[i]);
    }
    for(i=0;iedge;i++)
    {
        printf("请输入(vi-vj)和权重：");
        scanf("%d %d %d",&G->p[i].v1,&G->p[i].v2,&G->p[i].weight);
    }
    for(i=0 ;iedge;i++)				//冒泡排序法，权重从小到大存在边集数组中
    {
        for(j=G->edge-1;j>i;j--)
        {
            if(G->p[i].weight>G->p[j].weight)
            {
                G->p[G->edge]=G->p[i];
                G->p[i]=G->p[j];
                G->p[j]=G->p[G->edge];
            }
        }
    }
}
#克鲁斯卡尔算法
int Find(int *parent,int g)				//通过parent[]找到可连接的边
{
    while(parent[g]!=0)
    {
        g=parent[g];
    }
    return g;
}
int Finish(ALGraph *G,int *parent)		//判断生成树是否完成，完成的标志是生成树的边等于顶点的数量减1
{
    int i,n=0;

    for(i=0;ipeak;i++)
    {
        if(parent[i])
        {
            n++;
        }
    }
    if(n==G->peak-1)
    {
        return 1;
    }
    return 0;
}
int FindPeak(ALGraph *G,int g)		//找到顶点的下标
{
    int i;
    for(i=0;ipeak;i++)
    {
        if(G->m[i]==g)
            return i;
    }
    return -1;
}
void MinTree_Kruskal(ALGraph *G)
{
    int i,a,b;

    int parent[G->peak];

    for(i=0;ipeak;i++)		//初始化parent[]
    {
        parent[i]=0;
    }
    for(i=0;iedge;i++)
    {
        a=Find(parent,FindPeak(G,G->p[i].v1));
        b=Find(parent,FindPeak(G,G->p[i].v2));

        if(a!=b)				//如果a==b则表是a和b在同一颗生成树上，如果a和b连接则为生成环，不符合生成树
        {
            parent[a]=b;
            printf("%d->%d   %d\n",G->p[i].v1,G->p[i].v2,G->p[i].weight);
        }
        if(Finish(G,parent))		//完成后返回
        {
            return;
        }
    }
}

2. 普里姆(prim)算法思想

普里姆方法的思想是：在图中任取一个顶点K作为开始点，令U={k}，W=V-U，其中V为图中所有顶点集，然后找一个顶点在U中，另一个顶点在W中的边中最短的一条，找到后，将该边作为最小生成树的树边保存起来，并将该边顶点全部加入U集合中，并从W中删去这些顶点，然后重新调整U中顶点到W中顶点的距离, 使之保持最小，再重复此过程，直到W为空集止。

#define INFINITE 9999
#define MAXN 100
void prim(int cost[][MAXN],int n,int v)
{  
	int lowcost[MAXN],min,closest[MAXN],i,j,k;
	for(i=1;i<=n;i++)
    {  
		lowcost[i]=cost[v][i];
        closest[i]=v;
	}
   	for(i=1;i