119. 杨辉三角 II - 力扣（LeetCode）

题目描述

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。
在杨辉三角中，每个数是它左上方和右上方的数的和。

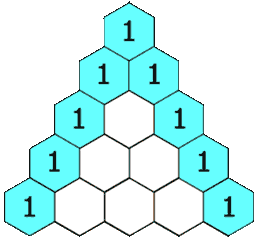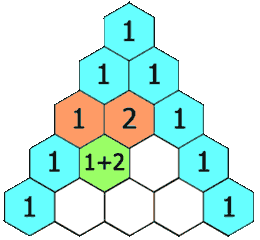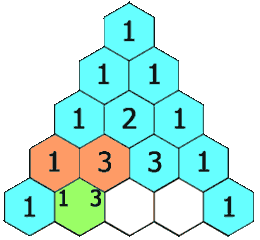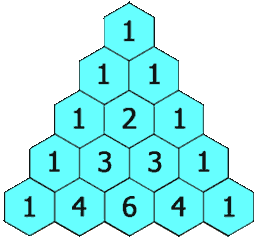
示例:
输入: 3
输出: [1,3,3,1]
进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

题解1

依据规律，通过上层求下层

代码1

/*
依据杨辉三角的规律，通过上层求下层
不同杨辉三角I的是我们不需要存储所有的结果，只需要用一个一维数组来存储
计算的时候从后往前算不会覆盖重复使用的值
时间复杂度为：O(n^2)
空间复杂度为：O(n)
*/
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int>res(rowIndex + 1, 1);
        if(rowIndex < 2){
            return res;
        }
        for(int i = 2; i < rowIndex + 1; ++i){
            for(int j = i - 1; j >= 1; --j){
                res[j] = res[j] + res[j - 1];
            }
        }
        return res;
    }
};

执行结果1

题解2

依据数学知识可知公式1。
rowIndex行的第j列元素值为
$$res[rowIndex][j]=C_{rowIndex}^j(j=0,1,2,\dots ,rowIndex)\text{\hspace{1em}(1)}$$
而$C_i^j$有公式2
$$C_i^j=\frac{i!}{(j!)(i-j)!}=\frac{(i-j+1)\ast (i-j+2)\ast \cdots \ast i}{j!}$$

代码2

/*
依据公式
*/
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int>res;
        long long int tmp = 1;
        res.push_back(1);
        for(int i = 1;i <= rowIndex; ++i){
            tmp = tmp * (rowIndex - i + 1) / i;
            res.push_back(tmp);
        }
        return res;
    }
};

执行结果2