漫画:有趣的扔鸡蛋问题
本文转载自程序员小灰
————— 第二天 —————
题目:扔鸡蛋问题
有2个鸡蛋,从100层楼上往下扔,以此来测试鸡蛋的硬度。比如鸡蛋在第9层没有摔碎,在第10层摔碎了,那么鸡蛋不会摔碎的临界点就是9层。
问:如何用最少的尝试次数,测试出鸡蛋不会摔碎的临界点?
举个栗子,最笨的测试方法是什么样呢?
把其中一个鸡蛋从第1层开始往下扔。
如果在第1层没碎,换到第2层扔
如果在第2层没碎,换到第3层扔
…
如果第59层没碎,换到第60层扔
如果第60层碎了,说明不会摔碎的临界点是第59层
在最坏情况下,这个方法需要扔100次。
方法一:二分法
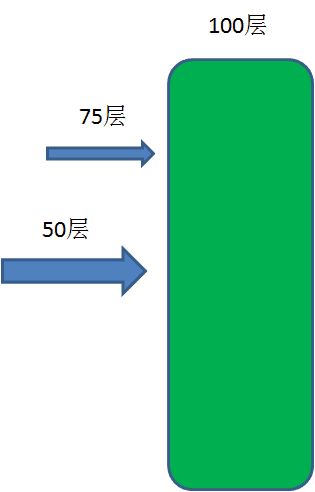
采用类似于二分查找的方法,把鸡蛋从一半楼层(50层)往下扔。
如果第一枚鸡蛋在50层碎了,第二枚鸡蛋就从第1层开始扔,一层一层增长,一直扔到第49层。
如果第一枚鸡蛋在50层没碎了,则继续使用二分法,在剩余楼层的一半(75层)往下扔…
这个方法在最坏情况下,需要尝试50次。
方法二:平方根法
如何让第一枚鸡蛋和第二枚鸡蛋的尝试次数尽可能均衡呢?
很简单,做一个平方根运算,100的平方根是10。
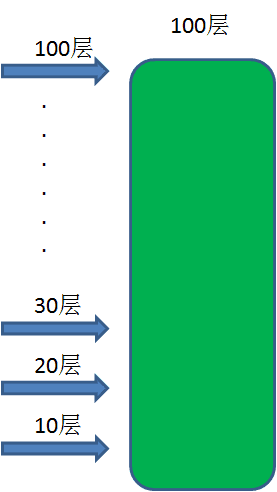
因此,我们尝试每10层扔一次,第一次从10层扔,第二次从20层扔,第三次从30层…一直扔到100层。
这样的最好情况是在第10层碎掉,尝试次数为 1 + 9 = 10次。
最坏的情况是在第100层碎掉,尝试次数为 10 + 9 = 19次。
不过,这里有一个小小的优化点,我们可以从15层开始扔,接下来从25层、35层扔…一直到95层。
这样最坏情况是在第95层碎掉,尝试次数为 9 + 9 = 18次。
————————————
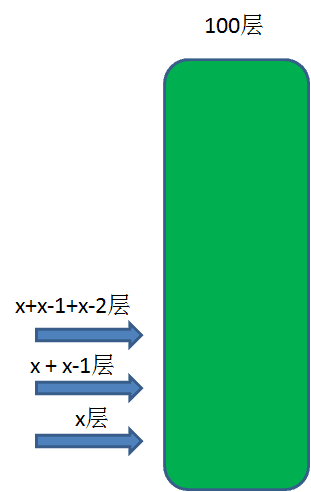
假设最优的尝试次数的x次,为什么第一次扔就要选择第x层呢?
这里的解释会有些烧脑,请小伙伴们坐稳扶好:
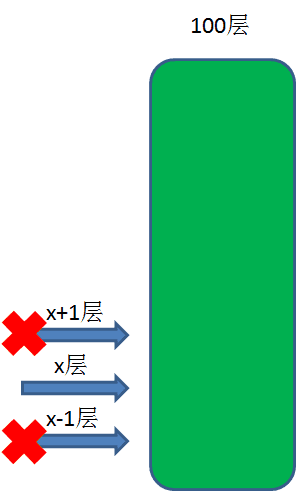
假设第一次扔在第x+1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x层。
这样一来,我们总共尝试了x+1次,和假设尝试x次相悖。由此可见,第一次扔的楼层必须小于x+1层。
假设第一次扔在第x-1层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x-2层。
这样一来,我们总共尝试了x-2+1 = x-1次,虽然没有超出假设次数,但似乎有些过于保守。
假设第一次扔在第x层:
如果第一个鸡蛋碎了,那么第二个鸡蛋只能从第1层开始一层一层扔,一直扔到第x-1层。
这样一来,我们总共尝试了x-1+1 = x次,刚刚好没有超出假设次数。
因此,要想尽量楼层跨度大一些,又要保证不超过假设的尝试次数x,那么第一次扔鸡蛋的最优选择就是第x层。
方法三:解方程法
x + (x-1) + (x-2) + … + 1 = 100
这个方程式不难理解:
左边的多项式是各次扔鸡蛋的楼层跨度之和。由于假设尝试x次,所以这个多项式共有x项。
右边是总的楼层数100。
下面我们来解这个方程:
x + (x-1) + (x-2) + … + 1 = 100 转化为
(x+1)*x/2 = 100
最终x向上取整,得到 x = 14
因此,最优解在最坏情况的尝试次数是14次,第一次扔鸡蛋的楼层也是14层。
最后,让我们把第一个鸡蛋没碎的情况下,所尝试的楼层数完整列举出来:
14,27, 39, 50, 60, 69, 77, 84, 90, 95, 99, 100
举个栗子验证下:
假如鸡蛋不会碎的临界点是65层,那么第一个鸡蛋扔出的楼层是14,27,50,60,69。这时候啪的一声碎了。
第二个鸡蛋继续,从61层开始,61,62,63,64,65,66,啪的一声碎了。
因此得到不会碎的临界点65层,总尝试次数是 6 + 6 = 12 < 14 。
隔壁寝室一块打羽毛球的同学在tplink二面中曾遇到过这道题,不过屏幕前的同学们不用担心,相必看到这里的同学应该彻底明白这道题是怎么一回事了。
更多关于本文的吐槽和讨论,评论中见哦**~**
—————END—————
扫描下方二维码,及时获取更多互联网求职面经、java、python、爬虫、大数据等技术,和海量资料分享:公众号后台回复“csdn”即可免费领取【csdn】和【百度文库】下载服务;公众号后台回复“资料”:即可领取5T精品学习资料、java面试考点和java面经总结,以及几十个java、大数据项目,资料很全,你想找的几乎都有
![]()
推荐阅读
【腾讯面试题】微信抢红包算法:源码+图+视频