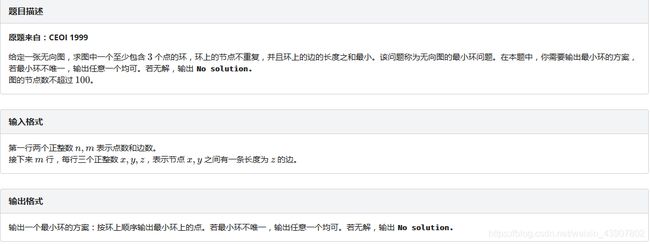
【Floyd求无向图最小环】一本通 3.2 例 1」Sightseeing Trip

analysis

思路

这算是弗洛伊德的一个活用版本了

这个模式就是图中求最小环的长度和方案,然后时间复杂度必须要允许

思路就是枚举一个k和和它相邻的两个点，看这三个点能否构成一个最小环

但是注意,因为找环的时候是保证了环中出现的点在k以内且经过点k的,而且不能出现把一条链来回走然后把这种方案当做一个环的情况

因此在找环的时候枚举i,j的时候应该

    loop(k,1,n){
		loop(i,1,k-1){
			loop(j,i+1,k-1){
				if(d[i][j]+a[k][i]+a[j][k]<minn){
					minn=d[i][j]+a[i][k]+a[k][j];
				}
			}
		}

这样的话就可以避免一条链来回走和某个点走过两次的情况

而且要先找环再Floyd更新d数组,这样可以保证环中出现的点在k以内

但是如果不这样会不会有问题呢?

如果这样的话,d[i][j]就会保存的是经过编号不超过k的节点,从i到j的最短距离

那么就会出现把一条链来回走然后把这种方案当做一个环的情况

输出方案数

Floyd记录路径,可以用这种方法:

	loop(k,1,n)    
		loop(i,1,n)
				loop(j,1,n)
					if(d[i][j]>d[i][k]+d[k][j])
						d[i][j]=d[i][k]+d[k][j],
						pos[i][j]=k;

这样的话,pos[i][j]就是存的i到j最短路会经过的点

这个数组如果值为0,那么说明什么呢?

说明i==j或者i和j的直接连边的长度小于所有的间接连边

那么我们如何得到i到j最短路径上的所有点呢?

$$这个时候分析一下,i到j的最短路径上的所有点,就等于i到pos[i][j]上的所有点(不包括pos[i][j])加上pos[i][j]到j上的所有点(不包括j)再加上j$$

诶,这不就是分治嘛,用递归实现啊

子问题和原问题一模一样啊:

设calc(i,j)返回i到j(不包括j)的最短路上的所有点
那么这个东西就等于calc(i,pos[i][j])+calc(pos[i][j]+j)+j
边界条件就是什么呢???
显然是当i和pos[i][j]一样的时候啊
不对,pos[i][j]不可能和i一样吧
那就考虑倒数第二步,当i和j中间仅隔了0个点时会怎样
这个时刻可以判断,就是pos[i][j]==0
如果到了这个时候,calc(i,j)就可以只操作一个事情了,就是把i放入记录的数组中(因为不包括j嘛)
于是代码应该这样写

    int res[maxn]
	int nfp=0;
	void calc(int u,int v){
		if(pos[u][v]==0){
			res[++nfp]=u;
			return;		
		}
		calc(u,pos[u][v]);
		calc(pos[u][v],v);
	}
	loop(k,1,n)
		loop(i,1,n)
			loop(j,1,n){
				if(d[i][k]+d[k][j]<d[i][j]){
					d[i][j]=d[i][k]+d[k][j];
					pos[i][j]=k;
				}			
			}
	calc(x,y);
	res[++nfp]=y;
	loop(i,1,nfp)
		printf("%d\n",res[i]);

关于为什么这里仅用pos[i][j]=k;

而不把i和j翻转一下的原因,在于i,j在循环中是从1~n的,也就是说如果

pos[i][j]=k

那么后面更新j到i的时候

pos[j][i]也一定会等于k

code

#include
using namespace std;
#define loop(i,start,end) for(register int i=start;i<=end;++i)
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define copy(arry,arry2) memcpy(arry,arry2,sizeof(arry))
#define ll long long 

template<typename T>void rd(T &x){
	x=0;char r=getchar();T neg=1;
	while(r>'9'||r<'0'){if(r=='-')neg=-1;r=getchar();}
	while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=getchar();}
	x*=neg;
}
#define inf 0x3f3f3f3f
int n,m;
const int maxn=100+10;
int G[maxn][maxn];
int D[maxn][maxn];
int path[maxn][maxn];
int minn=inf;
int _list[maxn];
int nfp=0;

inline void findpath(int u,int v){
	if(path[u][v]==0){
		_list[++nfp]=u;
		return;
	}
	findpath(u,path[u][v]);
	findpath(path[u][v],v);
}

inline void work(){
	copy(D,G);
	loop(k,1,n){
		loop(i,1,k-1){
			loop(j,i+1,k-1){
				if((ll)D[i][j]+G[k][i]+G[j][k]<minn){
					minn=D[i][j]+G[i][k]+G[k][j];
					nfp=0;
					findpath(i,j);
					_list[++nfp]=j;
					_list[++nfp]=k;
				}
			}
		}
		loop(i,1,n){
			loop(j,1,n){
				if(D[i][j]>D[i][k]+D[k][j]){
					D[i][j]=D[i][k]+D[k][j];
					path[i][j]=path[j][i]=k;
				}
			}
		}
	}
	if(minn>=inf)
		printf("No solution.\n");
	else
		loop(i,1,nfp)
			printf("%d ",_list[i]);
}

int main(){
	#ifndef ONLINE_JUDGE
	freopen("datain.txt","r",stdin);
	#endif
	clean(G,0x3f);
	clean(D,0x3f);
	
	rd(n);
	rd(m);
	loop(i,1,m){
		int xi,yi,zi;
		rd(xi);
		rd(yi);
		rd(zi);
		G[xi][yi]=min(G[xi][yi],zi);
		G[yi][xi]=min(G[yi][xi],zi);
	}	
	
	work();
	return 0;
}