解压缩软件
解压缩软件
一、实验目的和要求
利用哈夫曼树编码写出一个解压缩软件
二、实验环境
DEVC++ qt
三、实验内容
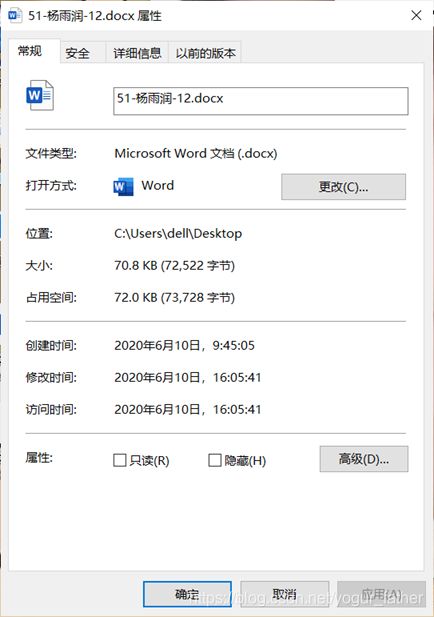
(1)压缩对象为外存任意格式任意位置的文件。
(2)运行时,压缩原文件的规模应不小于5K。运行后,外存上保留压缩后的文件。
(3)提供解压文件与原文件的相同性对比功能。
(4)建议,形成带交互界面功能的系统。
四、实验过程
4.1 任务定义和问题分析
①建立哈夫曼树
②利用文件流进行文件操作
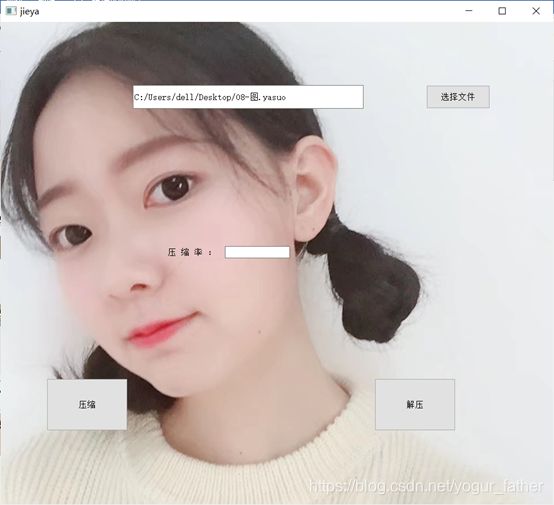
③设计交互界面
4.2 数据结构的选择和概要设计
哈夫曼树
4.3 详细设计
4.3.1创建一个哈夫曼树结点
建立一个哈夫曼树的结点,要在结点中我们设定一个权值key,左孩子,右孩子,父节点,这个父节点方便在之后进行树的创建。
struct node
{
int key;
int lkid,rkid,parent;
};
4.3.2 建立所需函数
寻找权值最小的两个数
统计字符出现的频率
创建哈夫曼树的函数
创建哈夫曼编码的函数
解压函数
压缩函数
4.3.3 创建哈夫曼树
①哈夫曼树的创建过程需要一个排序的过程,每次找出权值最小的两个结点。先在没有被建立成树的结点中标记一个m1和m2,再遍历找比m1小的,找到以后将这个结点标记为m1,再找第二小的,标记为m2,从而找到最小的两个结点。
②哈夫曼树权值的大小也就是他出现的频率,利用上面的排序,找出最小的两个结点m1和m2,将他们组成一个家庭,将他们的权值之和赋值给父节点。
③对这个结点进行哈夫曼编码,左0右1。我们设定一个标记p,如果结点p的父亲的左孩子是p的话,给p这个节点的哈夫曼编码加0,他父节点的右孩子是p的话,就给他的哈夫曼编码加1。最后将这个标记p标为p的父节点。
4.3.4 统计从文件读出的字符串总共有多少种字符,同时统计这些字符的频率
我们用字符的ascii码作为频率数组的下标,从文件中读出的字符串为str,一个一个遍历str,如果一个字符出现一次,给它对应的ascii作为下标的频率数组加一。最后再遍历一次,如果f [i]!=0,证明有字符串,给总数n加一,作为统计的字符串总数,也就是哈夫曼树的结点数。
4.3.5 将哈夫曼码转为等长二进制码
我们压缩的想法是,将哈夫曼码每八位做为一个单位,这八位二进制码的十进制对应的ascii码又对应一个字符,最后将所有的字符放在一起,写入压缩文件,达到压缩的效果。这个函数让每一种字符对应的ascii码都有对应的等长二进制码,方便后面压缩。每八位作为一个单位,不足八位的用0补齐。
4.3.6 压缩函数
①首先打开文件,同时获取文件名。将文件名截取为名字部分,和文件格式部分,方便之后压缩和解压命名文件名。
②用二进制打开文件后,用
f1.seekg(0,ios::end);
int l=f1.tellg();
来获取文件大小,之后创建一个字符串s来存放文件读出的字符串。
③统计字符串中的总字符种类,频率。再利用函数创建哈夫曼树,哈夫曼编码。再创建一个数组w用来放各个字符的频率。这个时候w的下标就是之前各个字符的ASCII码。
④创建一个string code,用来将所有的哈夫曼编码连起来,之前adr [256]的值,这样利用adr [256]我们就能找到hufcode的值,因为code的下标就是adr[256]。连起来就是,只要知道字符,就能知道他对应的哈夫曼编码。
⑤现在我们就得到了哈夫曼的编码,然后继续按每八位一个单位,不足8位的用0补齐。
⑥再创建一个新字符串 ns来储存新的压缩的字符串,将上面的code每八位处理一次,每八位的字符串赋值给s,s 经过ezs()函数,也就是二转十进制,得到一个数字,最后将这个数字根基ascii码转换为字符,再将这个字符赋值给ns,再一次处理后面的code,就得到了新压缩后的字符。
⑦之后我们还要把这个文件的类型,大小,每个字符的权值等信息写进去,方便后面解压。在设定一个结束的符号,最后加上之前的ns。
⑧打开一个新文件,将ns读进去。
⑨再读取这个文件的大小,计算压缩率。
4.3.7 解压函数
①同样的方法打开文件,获取字符串s,处理文件名。
注:这里有个函数,因为在之前的压缩函数中,我们将文件类型,字符的权值也写进去,因此我们要通过一个函数来截取这些信息。这些信息在之前设立的结束标识符之前。遍历到这个标识符结束就行。再按照文件大小,类型,字符,字符,频率截取就行。这样才能进行后面的解压操作。
②遍历s,获取每个字符的ascii码,再获取每个字符对应的等长二进制码。
③继续通过频率f []!=0,来获取哈夫曼树的结点数。
④创建哈夫曼数,写哈夫曼编码。这里的哈夫曼编码相当与一个查询表。
⑤获取哈夫曼树权值最大的结点,他的哈夫曼编码是最短的,后面读到的哈夫曼编码只要不小于这个长度,再来遍历是否有对应的字符。因此要不断遍历读取由文件中字符串转化为的二进制码,一个一个寻找哈夫曼编码对应的字符。如果找到一个和哈夫曼编码相同的哈夫曼码,这个哈夫曼的下标就是这个字符的ascii码,就知道了他的字符,将这个字符加入ns。
⑥这个ns的长度也就是源文件的长度。将之前获得的文件名,文件类型读出,创建文件。
五、测试及结果分析
5.1 实验数据
5.2 结果及分析
六、实验收获
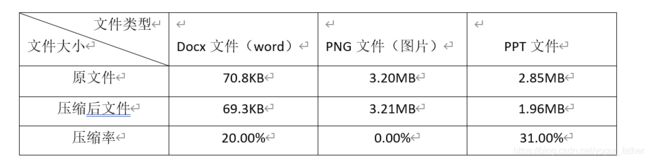
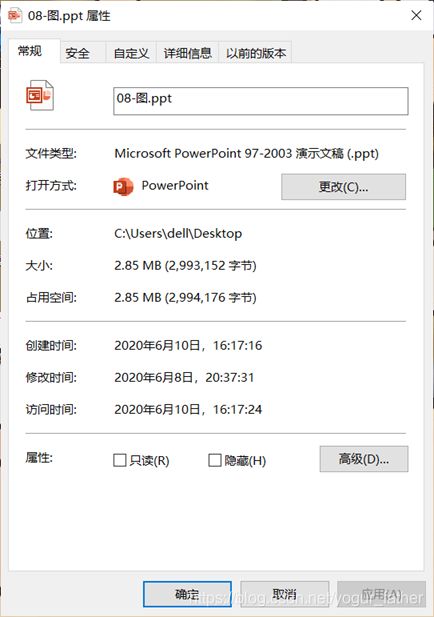
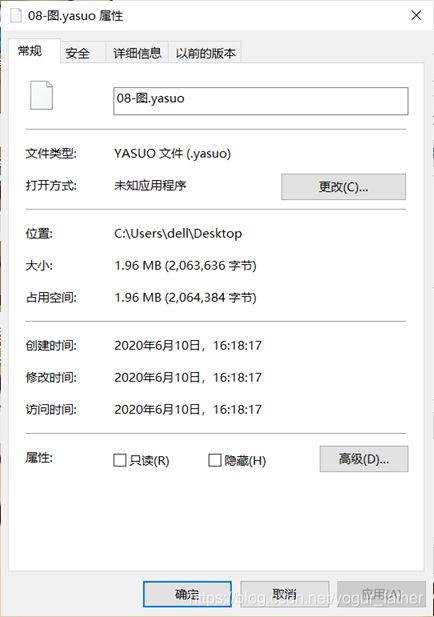
从这个代码中可以看出,有的问价压缩率比较客观,但有的文件压缩效果不是很好,比如图片文件格式,有可能会比以前的文件稍大一点,但对于大一点的文件来说效果就好很多。具体原因可能是在压缩的时候写入了字符频率,文件大小的原因,导致本来就很小的文件,在压缩空间很小的条件下,有写入了部分信息,导致文件变大。

经测试,发现图片类(JPG文件)的文件压缩率都不高,几乎都为0。咨询过同学后发现他们也有这种问题。这种越压缩越大可能是哈夫曼树压缩的弊端,对于部分类型的文件压缩效果一般。如果用其他算法压缩文件或许可以解决这个问题。
#include
type=filename.substr(i+1);
//cout<
break;
}
int n;
ifstream f1;
char* fn=(char*)filename.data();
f1.open(fn,ifstream::binary);
f1.seekg(0,ios::end);
int l=f1.tellg();
f1.seekg(0,ios::beg);
char* str=new char[l];
f1.read(str,l);
f1.close();
tongji(str,l,n);
element* hufftree=new element[2*n-1];//哈夫曼树共有2n-1个节点
string h_code[n];//ascii码对应的权值code[dictionaries[index]] index范围为0-255 0-127是正常的 128-255另作转换
int* w=new int[n];
int k=0;
for(int i=0;i<256;i++)//将零散分布的freq放入到整齐的w[k]
if(freq[i]!=0)
{
w[k]=freq[i];//w是权
dictionaries[i]=k;
k++;
}
huffman_tree(hufftree,w,n);//构建哈夫曼树
/*for(int i=0;i<2*n-1;i++)
cout<
huffman_code(hufftree,n,h_code);//根据哈夫曼树生成每个字符对应的哈夫曼编码
/*for(int i=0;i
if(n==1)
h_code[0]='0';
//cout<
string code="";
for(int i=0;i<l;i++)
{
int ascii=str[i];
if(ascii>=0)
code+=h_code[dictionaries[ascii]];
else
code+=h_code[dictionaries[ascii*-1+127]];
}
//cout<<"step2\n";
int len=code.length();
//cout<
//cout<
if(len%8!=0)//不够八位的补上0
{
int complement=8-l%8;
for(int i=0;i<complement;i++)
code+='0';
}
//cout<<"step3\n";
string newstr="";//压缩后的新字符串
for(int i=0;i*8<len;i++)
{
string s="";
for(int j=0;j<8;j++)//获得八位二进制码
s+=code[i*8+j];
int index=ezs(s);//转化为十进制 八位二进制生成一个字节
//cout<
if(index<128)
newstr+=char(index);
else
newstr+=char((index-127)*-1);
}
string prefix;
prefix+=type+'|';
prefix+=i_to_s(l);//前缀 解压时用
for(int i=0;i<256;i++)
{
if(freq[i]!=0)
{
prefix+='|';//字符前后用||分隔
if(i<128)
prefix+=char(i);
else
prefix+=char((i-127)*-1);
prefix+=i_to_s(freq[i]);
}
}
prefix+='|';
prefix+="stop";
newstr=prefix+newstr;
//cout<
l=newstr.length();
//cout<
//cout<
string lmyfile=name+".yasuo";
char* lf=(char*)lmyfile.data();
ofstream f2;
f2.open(lf,ofstream::binary);
const char* a=newstr.data();
f2.write(a,l);
f2.close();
delete[] hufftree;
delete[] w;
delete[] str;
}
void decompress()
{
string filename;
cout<<"输入要解压文件的完整路径"<<endl;
cin>>filename;
int fl=filename.length();
for(int i=0;i<fl;i++)
if(filename[i]=='\\')
{
filename.insert(i,"\\\\");
i+=2;
}
for(int i=0;i<256;i++)
equal_length_code[i]=dcr(i);
for(int i=0;i<256;i++)
freq[i]=0;
for(int i=0;i<256;i++)
dictionaries[i]=-1;
string hc[256];
string name;
string type;
for(int i=filename.length()-1;i>=0;i--)
{
if(filename[i]=='.')
{
name=filename.substr(0,i);
break;
}
}
//cout<
ifstream f1;
char* fn=(char*)filename.data();
f1.open(fn,ifstream::binary);
f1.seekg(0,ios::end);
int l=f1.tellg();
f1.seekg(0,ios::beg);
char* str=new char[l];
f1.read(str,l);
f1.close();
int len;//字符的总数
int begin=getprefix(str,l,type,len);//begin是新的下标
string code="";
for(int i=begin;i<l;i++)
{
int ascii=str[i];
if(ascii>=0)
code+=equal_length_code[ascii];
else
code+=equal_length_code[ascii*-1+127];
}
//cout<
int n=0;//原哈夫曼树叶子节点个数
for(int i=0;i<256;i++)
if(freq[i]!=0)
n++;
element* hufftree=new element[2*n-1];//哈夫曼树共有2n-1个节点
string h_code[n];//index范围为0-255 0-127是正常的 128-255另作转换
int* w=new int[n];
int k=0;
for(int i=0;i<256;i++)//将零散分布的freq放入到整齐的w[k]
if(freq[i]!=0)
{
w[k]=freq[i];//w是权
dictionaries[i]=k;
k++;
}
huffman_tree(hufftree,w,n);//构建哈夫曼树
/*for(int i=0;i<2*n-1;i++)
cout<
huffman_code(hufftree,n,h_code);//根据哈夫曼树生成每个字符对应的哈夫曼编码
/*for(int i=0;i
if(n==1)
h_code[0]='0';
for(int i=0;i<256;i++)
if(freq[i]!=0)
hc[i]=h_code[dictionaries[i]];
int cl=code.length();
string newstr="";
int a=0;//遍历数组code的下标
int max=0;//设max是出现频率最高的字符的下标
for(int i=1;i<256;i++)
if(freq[i]>freq[max])
max=i;
int min_length=h_code[dictionaries[max]].length();
//cout<
for(int k=0;k<len;k++)//len原文件的字符数
{
string temp="";//不断读取code中的二进制码 找到哈夫曼编码
while(a<cl)
{
bool found=false;
temp+=code[a];
if(temp.length()<min_length)
{
a++;
continue;
}
for(int index=0;index<256;index++)
{
if(temp==hc[index])
{
found=true;
if(index<128)
newstr+=char(index);
else
newstr+=char((index-127)*-1);
break;
}
}
a++;
if(found==true)
break;
}
}
l=newstr.length();//原文件长度
const char* b=newstr.data();
string lmyfile=name+'.'+type;
char* lf=(char*)lmyfile.data();
ofstream f2;
f2.open(lf,ofstream::binary);
f2.write(b,l);
f2.close();
delete[] str;
delete[] w;
delete[] hufftree;
}
int ezs(string code)
{
int l=code.length();
int result=0;
for(int i=0;i<l;i++)
if(code[i]=='1')
result+=pow(2,l-i-1);
return result;
}
string i_to_s(int l)
{
string str="";
while(l>=10)
{
str=char(l%10+48)+str;
l/=10;
}
str=char(l+48)+str;
return str;
}
int s_to_i(string str)
{
int n=0;
for(int i=0;i<str.length();i++)
n=n*10+int(str[i]-48);
return n;
}
int getprefix(char *str,int l,string &type,int &len)
{
string newstr;
//cout<
int e=0;//结束标志stop开始的地方
for(int i=0;i<l;i++)
if(str[i]=='s'&&str[i+1]=='t'&&str[i+2]=='o'&&str[i+3]=='p')
e=i;
//cout<
int i=0;
int front,rear;
for(i;i<e;i++)
if(str[i]=='|')
{
rear=i;
type=getstr(str,0,rear);
i++;
break;
}
//cout<
front=rear+1;
for(i;i<e;i++)
if(str[i]=='|')
{
rear=i;
len=s_to_i(getstr(str,front,rear-front));
break;
}
//cout<
//cout<
while(i<e)
{
if(str[i]=='|')
{
int w;
i++;
if(i>=e)
break;
int ascii=str[i];
i++;
front=i;
for(i;i<e;i++)
{
if(str[i]=='|')
{
rear=i;
w=s_to_i(getstr(str,front,rear-front));
break;
}
}
if(ascii>=0)
freq[ascii]=w;
else
freq[ascii*-1+127]=w;
}
}
return e+4;
}
string getstr(char* str,int begin,int l)
{
string s="";
for(int i=begin;i<begin+l;i++)
s+=str[i];
return s;
}