输出格式:
按照"{ v1 v2 ... vk }"的格式,每行输出一个连通集。先输出DFS的结果,再输出BFS的结果。
输入样例:
8 6
0 7
0 1
2 0
4 1
2 4
3 5
输出样例:
{ 0 1 4 2 7 }
{ 3 5 }
{ 6 }
{ 0 1 2 7 4 }
{ 3 5 }
{ 6 }
打算分别写用邻接矩阵和邻接表实现。目前写完邻接矩阵的
关于:void(*VisitFunc)(VertexType v); 来自:https://zhidao.baidu.com/question/349140172.html 的其中一个回答:
void(*VisitFunc)(VertexType v);
1,按运算符优先级, VisitFunc 先与* 结合, 说明VisitFunc是个指针
2,然后(*VisitFunc) 与后面的 ()结合, 说明*VisitFunc 是个函数
总结: VisitFunc 是个指向函数的指针, 函数的返回类型是void, 参数的类型是VertexType
问:
void Visit( Vertex V )
{
printf("正在访问顶点%d\n", V);
}
void DFS( MGraph Graph, Vertex S, void (*Visit)(Vertex) );
void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) );
两个搜索函数都传入了visit函数的原因是?
老师的解答:这样使访问visit可以用户自己定义(比如,不一定是printf,也许需要把结点的值累加起来)
代码参考链接:https://www.cnblogs.com/masterchd/p/7801841.html(非常感谢!
感想:
- 输出格式{ v1 v2 v3 }费了些时间来调。还要求每输出完一组就换行,那个换行符要调
- 本次代码涉及的东西有点多,还有队列,正好趁此机会复习了一下。
- 写代码首先把大致的模块(用到的函数)写出来,再去补充和完善各个函数
- 其实中途有点瓶颈,但后来发现我绕过去了。就是ListComponents_DFS与DFS,一开始以为主函数用DFS,但后面发现“进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。”这个要求很难弄,但我没死磕,反而接着写连通的函数ListComponents_DFS,发现原来主函数用ListComponents_DFS即可。
- 那个Visited[]数组,需要设两个。因为DFS和BFS分别都要,如果只设一个的话,DFS用完,整个数组是全置了1的,除非DFS用完后置0,或者BFS判断时反向判断,都行~
- Graph=(MGraph)malloc(sizeof(struct GNode));与E=(Edge)malloc(sizeof(struct ENode)); 需要加这两个,不然在dev上运行会出错,原因未知...
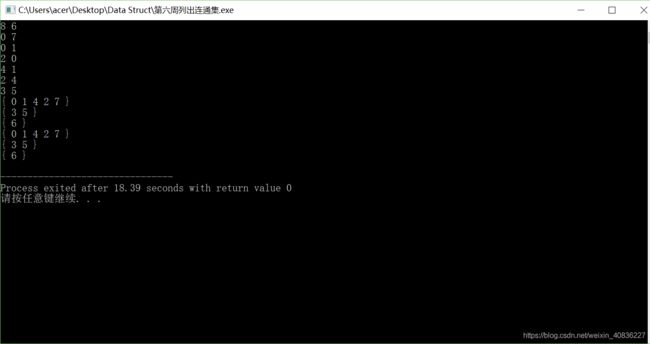
- 如果BFS中也用递归会如何?答:(结果如图)那队列没有存在的意义了,for循环也没有。因为队列只会存一个元素,存了一个,出来一个,又存一个。所以,会和DFS一样
/*DFS*/
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex V) ){
Vertex W;
Visited_DFS[V] = 1;
Visit(V);
for(W = 0; W < Graph->Nv ; W++)
{
if(Graph->G[V][W] ==1 && !Visited_DFS[W])
{
DFS(Graph, W, Visit);
}
}
return;
}
/*BFS*/
void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) ){
Queue Q;
Vertex V,W;
Q=CreateQueue();//MaxSize
Visit(S);
Visited_BFS[S]=1;
AddQ(Q,S);
while(Q->front!=NULL){
V=DeleteQ(Q);
for(W=0; WNv; W++){
if(Graph->G[V][W]==1 && !Visited_BFS[W]){
BFS(Graph, W, Visit); //若将下面三行换成此行,会如何?
// Visit(W);
// Visited_BFS[W]=1;
// AddQ(Q,W);
}
}
}
}
邻接矩阵源码:
/*邻接矩阵实现*/
#include
#include
#define MaxVertexNum 10
#define MaxSize 10
typedef int WeightType;
typedef int Vertex;
typedef int ElementType;
int Visited_DFS[MaxVertexNum]; /* 顶点的访问标记 */
int Visited_BFS[MaxVertexNum];
struct GNode{
int Nv;
int Ne;
WeightType G[MaxVertexNum][MaxVertexNum];
};
typedef struct GNode *PtrToGNode;
typedef PtrToGNode MGraph;
struct ENode{
Vertex V1,V2;
WeightType Weight;
};
typedef struct ENode *PtrToENode;
typedef PtrToENode Edge;
struct Node{
ElementType Data;
struct Node *Next;
};
struct QNode{
struct Node *front;
struct Node *rear;
};
typedef struct QNode *Queue;
MGraph CreateGraph(int VertexNum);
void InsertEdge(MGraph,Edge E);
MGraph BuildGraph();
void Visit( Vertex V );
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );
void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) );
void ListComponents_DFS(MGraph Graph);
void ListComponents_BFS(MGraph Graph);
Queue CreateQueue();
void AddQ(Queue Q,Vertex S);
ElementType DeleteQ(Queue Q);
int main(void){
MGraph Graph;
Vertex V;
Graph=BuildGraph();
// DFS(Graph,V,Visit);
ListComponents_DFS(Graph);
// BFS(Graph,V,Visit);
ListComponents_BFS(Graph);
return 0;
}
/*MGraph初始化*/
MGraph CreateGraph(int VertexNum){
Vertex V,W;
MGraph Graph;
//需加(MGraph)
Graph=(MGraph)malloc(sizeof(struct GNode));
Graph->Nv=VertexNum;
Graph->Ne=0;
for(V=0;VNv;V++)
for(W=0;WNv;W++)
Graph->G[V][W]=0;
return Graph;
}
/*MGraph插入边*/
void InsertEdge(MGraph Graph,Edge E){
Graph->G[E->V1][E->V2]=E->Weight;
Graph->G[E->V2][E->V1]=E->Weight;
}
/*完整建立MGraph*/
MGraph BuildGraph(){
MGraph Graph;
Edge E; Vertex V; int Nv, i;
scanf("%d",&Nv);
Graph=CreateGraph(Nv);
scanf("%d",&(Graph->Ne));
if(Graph->Ne != 0){
//需加(Edge)
E=(Edge)malloc(sizeof(struct ENode));
for(i=0; iNe; i++){
scanf("%d %d",&E->V1, &E->V2);
E->Weight=1;
InsertEdge(Graph, E);
}
}
for(V=0; VNv; V++){
Visited_BFS[V]=0;
Visited_DFS[V]=0;
}
return Graph;
}
/*访问节点*/
void Visit( Vertex V ){
printf(" %d", V);
}
/*DFS连通*/
void ListComponents_DFS(MGraph Graph){
Vertex i;
for(i=0; iNv; i++){
if(!Visited_DFS[i]){//节点i未被访问过
printf("{");
DFS(Graph, i, Visit);
printf(" }");
printf("\n");
}
}
}
/*BFS连通*/
void ListComponents_BFS(MGraph Graph){
Vertex i;
for(i=0; iNv; i++){
if(!Visited_BFS[i]){
printf("{");
BFS(Graph, i, Visit);
printf(" }");
printf("\n");
}
}
// printf("\n");
}
/*
进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。How??
按照"{v1v2...vk}"的格式,每行输出一个连通集。
*/
/*DFS*/
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex V) ){
Vertex W;
Visited_DFS[V] = 1;
// printf("{");
Visit(V);
for(W = 0; W < Graph->Nv ; W++)
{
if(Graph->G[V][W] ==1 && !Visited_DFS[W])
{
DFS(Graph, W, Visit);
}
}
// printf("}");
return;
}
/*BFS*/
void BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) ){
Queue Q;
Vertex V,W;
Q=CreateQueue();//MaxSize
Visit(S);
Visited_BFS[S]=1;
AddQ(Q,S);
while(Q->front!=NULL){
V=DeleteQ(Q);
for(W=0; WNv; W++){
if(Graph->G[V][W]==1 && !Visited_BFS[W]){
Visit(W);
Visited_BFS[W]=1;
AddQ(Q,W);
}
}
}
}
/*建队列,假定为空*/
Queue CreateQueue(){
Queue Q;
Q=(Queue)malloc(sizeof(struct QNode));
Q->front=Q->rear=NULL;
return Q;
}
/*进队列*/
void AddQ(Queue Q,Vertex S){
struct Node *temp;
temp=(struct Node*)malloc(sizeof(struct Node));
temp->Data=S;
temp->Next=NULL;
if(Q->front==NULL){
Q->front=temp;
Q->rear=temp;
}
else{
Q->rear->Next=temp;
Q->rear=temp;
}
// return Q;
}
/*出队列*/
ElementType DeleteQ(Queue Q){
struct Node *FrontCell;
ElementType FrontElem;
if(Q->front==NULL){
return -1;
}
FrontCell=Q->front;
if(Q->front==Q->rear)
Q->front=Q->rear=NULL;
else Q->front=Q->front->Next;
FrontElem=FrontCell->Data;
free(FrontCell);
return FrontElem;
}
邻接表
实现思路:
- 要搞清楚Vertex 与 PtrToAdjVNode中AdjV的关系。
- 用邻接表写BFS时,遇到一个问题。题目要求:“进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。”从编号最小的顶点出发好说,在连通函数里用for循环遍历一遍就好了。但是后者,按递增顺序访问临界点,对邻接表来讲并不友好。因为邻接表的插入是利用G[V].FirstEdge的,而且与输入数据的顺序有关,所以插入之后,结点是随便排序的。本来想着能不能在BFS函数中进行调整,但是我没想到比较好的方法。简单粗暴就用遍历,但....太傻了,而且实现起来不是一般的麻烦,完全没必要。所以我觉得题目要求:“进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。”这个要求可能就已经限制我们要用邻接矩阵了。
- 邻接表的实现,我打算BFS那里是随机的,可以从编号最小出发,但不是按递增的顺序访问临界点(此处比个小心心~)
作业有点多,我先做作业了。代码写的差不多。先贴上来叭
/*用邻接表实现*/
#include
#include
#define MaxVertexNum 10
typedef int WeightType;
typedef int Vertex;
typedef int ElementType;
int Visited_DFS[MaxVertexNum]; /* 顶点的访问标记 */
int Visited_BFS[MaxVertexNum];
typedef struct AdjVNode *PtrToAdjVNode;/*PtrToAdjVNode需要在上面,可能是因为要先声明*/
struct AdjVNode{
Vertex AdjV;
WeightType Weight;
PtrToAdjVNode Next;//或者用struct AdjVNode *Next?
};
typedef struct VNode{
PtrToAdjVNode FirstEdge;
}AdjList[MaxVertexNum];
struct GNode{
int Nv;
int Ne;
AdjList G;
};
typedef struct GNode *PtrToGNode;
typedef PtrToGNode LGraph;
struct ENode{
Vertex V1,V2;
WeightType Weight;
};
typedef struct ENode *PtrToENode;
typedef PtrToENode Edge;
LGraph CreateGraph(int VertexNum);
void InsertEdge(LGraph Graph, Edge E);
LGraph BuildGraph();
void Visit( Vertex V );
void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) );
void BFS( LGraph Graph, Vertex S, void (*Visit)(Vertex) );
int main(void){
LGraph Graph;
Graph=BuildGraph();
return 0;
}
/*建空图*/
LGraph CreateGraph(int VertexNum){
Vertex V;
LGraph Graph;
Graph=(LGraph)malloc(sizeof(struct GNode));
Graph->Ne=0;
Graph->Nv=VertexNum;
for(V=0; VNv; V++)
Graph->G[V].FirstEdge=NULL;
return Graph;
}
/*插入边*/
void InsertEdge(LGraph Graph, Edge E){
PtrToAdjVNode NewNode1,NewNode2;
/*插入边*/
NewNode1=(PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode1->AdjV=E->V2;
NewNode1->Weight=E->Weight;
NewNode1->Next=Graph->G[E->V1].FirstEdge;
Graph->G[E->V1].FirstEdge=NewNode1;
/*插入边*/
NewNode2=(PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
NewNode2->AdjV=E->V1;
NewNode2->Weight=E->Weight;
NewNode2->Next=Graph->G[E->V2].FirstEdge;
Graph->G[E->V2].FirstEdge=NewNode2;
}
/*完整建立一个图*/
LGraph BuildGraph(){
LGraph Graph;
Edge E; Vertex V; int Nv, i;
scanf("%d",&Nv);
Graph=CreateGraph(Nv);
scanf("%d",&Graph->Ne);
if(Graph->Ne){
E=(Edge)malloc(sizeof(struct ENode));
for(i=0; iNe; i++){
scanf("%d %d",&E->V1,&E->V2);
E->Weight=1;
InsertEdge(Graph,E);
}
}
for(V=0; VNv; V++){
Visited_BFS[V]=0;
Visited_DFS[V]=0;
}
return Graph;
}
/*打印*/
void Visit( Vertex V ){
printf(" %d",V);
}
/*DFS*/
void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) ){
PtrToAdjVNode W;
Visit(V);
Visited_DFS[V]=1;
for(W=Graph->G[V].FirstEdge; W; W=W->Next){
if(!Visited_DFS[W->AdjV])
DFS(Graph, W->AdjV, Visit);
}
}
/*BFS 需重看,很巧妙的一个方法。没有用队列,数组就可以了。算拓展思维吧*/
void BFS( LGraph Graph, Vertex S, void (*Visit)(Vertex) ){
int queue[1010];
int l=0,r=0;
queue[r++]=S;
(*Visit)(S);
Visited[S]=true;
PtrToAdjVNode tmp;
while(l!=r)
{
tmp=Graph->G[queue[l++]].FirstEdge;
while(tmp)
{
Vertex pos=tmp->AdjV;
if(!Visited[pos])
{
Visit(pos);
Visited[pos]=true;
queue[r++]=pos;
}
tmp=tmp->Next;
}
}
}
