【数据结构】初入数据结构的树(Tree)以及Java代码实现(一)
初入数据结构的树(Tree)以及Java代码实现(一)
- 树的定义
- 为什么叫树?
- 树型结构的元素具有一对多关系
- 树的定义
- 树的一些基本概念
- 树的结点
- 后代,祖先
- 子树、空树
- 树的度与高(深度),结点的度与层次
- 有序树,无序树和森林
- 树的三种形式的Java代码实现
树的定义(Tree)
为什么叫树?
为什么叫树呢?因为将具有一对多关系的集合中的元素安装上图中的逻辑结构存储,整个存储形状从逻辑结构上看就像现实生活中一颗倒着生长的树,毕竟形象生动,所以这种数据结构也就被叫做树(Tree),这种存储结构也就成为树形存储结构
树型结构的元素具有一对多关系
我们之前了解的链表,数组,栈,队列都是一些线性存储的结构,数据关系也是简单的一对一关系,因为线性表中的每个数据元素都最多只有一个前驱和后继元素,不可能再多了,即线性表的某个节点的下一个元素,只有一种选择。

我们这里讲的树,则是一个非线性的存储结构,存储的是一对多关系的数据元素集合,为什么说是一对多呢?如上图,对于数节点A 来说,和节点 B、C有关系;对于节点 B 来说,和 A、D、E 有关系。换成线性表的概念来说,就是这个结点B有一个前驱节点A,还有两个后继节点D,E。即某个结点至多有一个前驱节点,但可能有多个后继节点,一个结点可能有对应多个后继节点,这就是树“一对多”的关系。

或者说如此解释,上图是用集合嵌套的方式表示一棵树,你看A可以囊括B,C两个数据,B可以囊括D,E两个数据,所以我们说树的数据是一对多的,对应的意义就是一个结点是可以有多个子结点的,不像线性表,它的下一个元素只有一种选择,树可能是有多种选择的
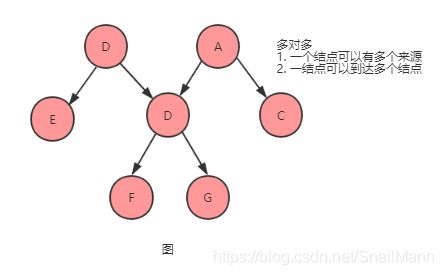
联想下图的多对多
对此我们再联想一下,为什么图的数据是多对多的?如果强行把图看做一颗树,那么这棵树的子树是可以相交的;即某棵树的结点A的下个元素可以是结点B或结点C,结点D下个元素可以是接点E或结点C,这里我们会发现不同的结点,他们的下个元素可以是同一结点C,此时该树就不能再叫树了,应该叫图。多对多的意思就是,同一个结点,可能有多个上一元素,也可以有多个下一元素,即从不同的结点出发,可以到达同一个结点,从同一结点出发,又可以到达不同的结点,这就是图的数据元素关系是多对多
树的定义
我们知道数据结构中的树,是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树, 那它的具体定义是什么呢?
百度百科的定义:
树(tree)是包含n(n>=0)个结点的有穷集,其中:
- 每个元素称为结点(node);
- 有一个特定的结点被称为根结点或树根(root)。
- 除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树(subtree)
简单的说就是,一颗树由根结点和m(m>=0)棵子树构成,或者说由n(n>=0)个结点构成一颗树
如果某棵树没有结点,即n = 0 ,那这就是一颗空树;即使只有一个结点,没有子树,依然可以构成一颗树,即n = 1,m = 0
树的种类

在基础树的前提下,再增加一些规则, 就形成了各式各样的树形存储结构,如上图就是树的各种变种和种类
树的一些基本概念
树的结点
结点
使用树形存储结构的每一个数据元素都被称为结点,不过在线性表中一般叫节点,所以别混了哟根结点
每一个非空树都有一个,也至少一个称为根的结点,它就是根结点,是树形结构的起点;如果某棵树的结点没有父结点,那么该结点就一定是根结点,所以整棵树,只有根结点没有父结点父结点(双亲节点)
树型结构的某个数据元素(结点)如果有后继节点,那么这个结点就是这些后继节点的父结点,或叫双亲结点子结点
树型结构的某个数据元素(结点)如果有前驱节点,那么这个结点就是这个前驱节点的子结点兄弟结点
树形结构中的某些数据元素(结点)如果具有通一个父结点,那么他们之间的关系就是兄弟结点叶子结点(叶结点)
树形结构中的某个结点,如果么有任何的子结点,那么该结点就被称为叶子结点(叶结点)分支结点
树形结构中不是根结点,也不是叶子结点的剩余结点都是分支结点,即至少有一个子结点的非根结点就是分支结点

从上图的树形存储结构来看,A,B,C,D,E,F,G,H元素都是树的结点,A是整棵树的根结点,A还是B,C的父结点(双亲结点),B,C则是A的子结点,B,C之间因为具有相同的父结点A,所以它们是兄弟结点关系; 而D,E,F,H则是这棵树的叶子节点, 因为这些结点没有子结点
注意:
但要注意的是,隔代不算父结点和子结点,即A不是D,E的父结点,D,E也不是A的子结点
后代,祖先
后代(Descendant)
就是从某个结点A开始,向下遍历所有可达的结点,这些可达的结点都是这个结点A的后代祖先(Ancestor)
就是从某个结点A开始,向上遍历所有可达的结点,这些可达的结点就是这个结点A的祖先
如上面图的展示,B,C,D,E,F,G,H这些结点都是根结点A的后代,F,G,H也是结点C的后代;反之结点A就是这棵树所有结点的祖先,结点C是F,G,H结点的祖先
子树、空树
什么是子树?
子树的定义
- 以
某棵树(1)的根结点(a)的子结点(b,c...)作为根结点的树就是这棵树(1)的子树
树的定义
- 除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树(subtree)
我们从树的定义中知道,每棵树都是由根节点以及m(m>=0)个互不相交的子树构成的;所以我们从下图中知道,树一如果是一个棵树,那么这棵树就是由根结点A和两颗子树(树二,树三)构成 ; 小技巧就是,要想知道一颗树拥有多少颗子树,就看该树根结点有多少个子结点就可以了,两者意思是查不多的
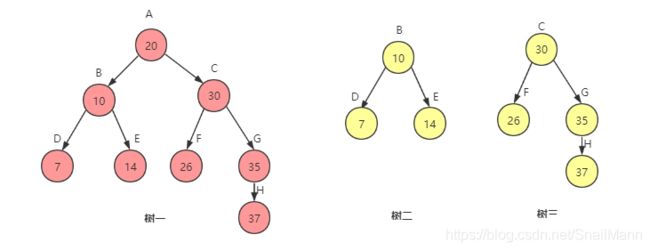
注意:
但是这里还是会有混淆人的地方,那就是G->H这棵树,算是树一的子树吗?答案就是不算,它算是树三的子树,但是不算树一的子树,我们可以重新回顾子树的定义,子树必须是某棵树根结点的子结点为根结点构成的树(的确很绕,慢慢理解就行)
什么是空树?
如果集合本身为空,即没有任何数据元素,即没有任何结点,那么我们就可以称这是一颗空树。也许你会疑惑,没有结点也能叫树?当然可以,我们回顾树的定义,树是有n(n>=0)个结点构成的,即n是可以等于0的奥,意思就是一颗树可以没有任何结点,我们称这种特殊的情况为空树
树的度与高(深度),结点的度与层次
树的度
一棵树中, 找到树中结点度的最大的那个结点,这个结点的度就是树的度,即树中各结点度的最大值称为该树的度树的高(深度)
该树的结点能到的最大层次就是该树的高,也即深度结点的度
一个结点拥有的子树的个数称为该节点的度结点的层次
从根开始定义起,根为第1层,根的子节点为第2层,以此类推

看上图,即根结点A的度是2;分支结点B的度也是2;分支结点G的度是1;叶子结点H的度是0。因为该树所有结点中,度最大就是2,所以该树的度是2,
A根结点是第一层,结点B,C是第二层,结点D,E,F,G是第三层,结点H是第四层;因为该树的结点能到达的最大层次就是4,所以该树高为4,即深度为4
有序树,无序树和森林
有序树和无序树
如果树中每个结点的子树从左到右看,谁在左边,谁在右边,是有规定的,那么这棵树就是有序树,反之则称为无序树;在有序树中,一个结点最左边的子树称为第一个孩子,最右边的称为最后一个孩子森林
由m(m >= 0)个互不相交的树组成的集合被称为森林;我们知道树可以理解为是由根结点和若干子树构成的,而这若干子树本身是一个森林,所以,树还可以理解为是由根结点和森林组成的; 所以树有一个式子可以表示:Tree = (root , F), root 即树的根节点,F表示由m(m>=0)棵树组成的森林
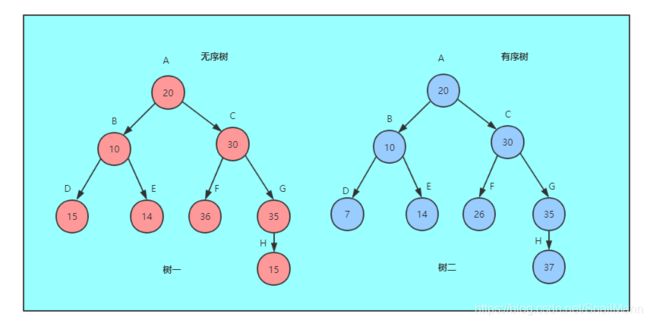
从上图,我们可以看到有两个树,他们长的样子是一样的,但是有树一是无序树,树二是有序树。
为什么树二是有序树呢? 首先回忆有序树的定义,从树的每一个结点的子树来看,子树在左还是在右是有规定的。我们再来看看树二,比如根结点A的两颗子树,我们会发现右子树的数据值肯定比左子树的值要大,再看结点B,同样,右子树的值肯定比左子树的值要大,其他结点也同样,所以我们才会说树二是一颗有序树。
那么树一为什么是无序树呢? 我们来看看,根结点A的右子树的数据值不一定左子树大奥,有想等的情况,比如结点D和结点H,你可能会说,我们的规则是大于等于。好,我们再看看, 结点B的右子树的数据值居然比左子树的值小奥,同理,结点C也存在同样的情况,所以我们会发现很难从树一中找出一个排列规律,所以我们可以认为它是一颗无序树
注意:
当然有些有序树的规则是非常复杂的,有时候这些规则并不是能马上看出来的,如规定第二层的结点右子树值要大于左子树,第三层的结点,左子树要大于右子树,第四层开始,右子树大于左子树,第五层…当然这个情况还是偏简单,还有更多复杂的规则就等你自己去探索啦
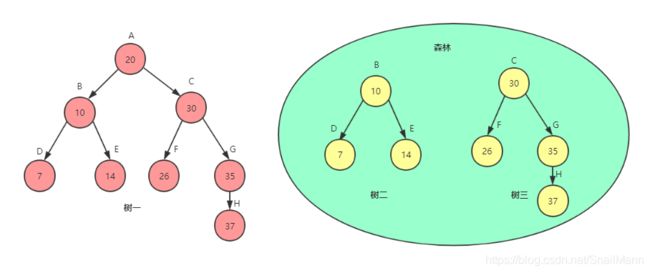
从上图,我们可以看到树一是一颗树,树一的子树就是树二和树三,树二和树三可以构成一个树集合,这个集合我们就称为森林; 所以树一就是由根结点A和这个森林构成的树
树的Java代码实现
请看 >>> 初入数据结构的树(Tree)以及Java代码实现(二)
参考资料
- 数据结构中的树存储结构 - @作者:解学武
- 数据结构与算法–树的三种存储结构 - @作者:sunhaiy
- 数据结构中各种树 - @作者:Poll
- Data Structure and Algorithms - Tree - @作者:tutorialspoint
- Tree (data structure) - @作者:wikipedia