学习Python已经有一段时间了,也学习了递归的方法,而能够实践该方法的当然就是汉诺塔问题了,但是这次我们不只是要完成对汉诺塔过程的计算,还要通过turtle库来体现汉诺塔中每一层移动的过程。
一、设计一个类(Class)
类(Class):用来描述具有相同的属性和方法的对象的集合。它定义了该集合中每个对象所共有的属性和方法。对象是类的实例。
下面是此程序需用到的类(Class)代码:
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - 1]
def size(self):
return len(self.itemsa)
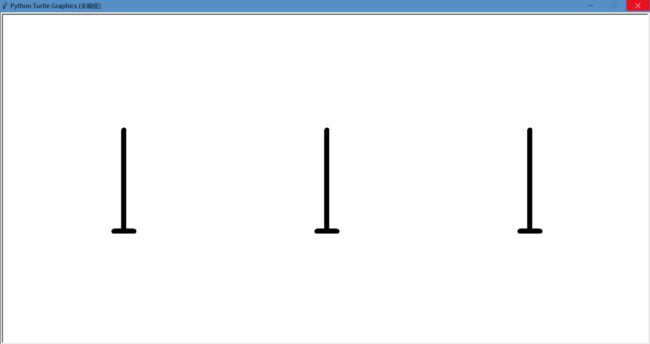
二、设计汉诺塔的底座
为了还原汉诺塔的移动过程,增强可视化程度,我们给它加上三个底座,代码如下:
def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize(10)
t.speed(100)
t.goto(400*(k-1), 100)
t.down()
t.goto(400*(k-1), -100)
t.goto(400*(k-1)-20, -100)
t.goto(400*(k-1)+20, -100)
drawpole_1(0)#画出汉诺塔的poles[0]
drawpole_1(1)#画出汉诺塔的poles[1]
drawpole_1(2)#画出汉诺塔的poles[2]
三、制造汉诺塔的盘子
汉诺塔当然少不了盘子了,我们要写一段代码来绘制若干个盘子,代码如下:
def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-400,-90+20*i)
plates[i].showturtle()
return plates
四、制造一个底座的栈
栈:栈作为一种数据结构,是一种只能在一端进行插入和删除操作。它按照先进后出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。
此处使用的栈并非Python中真正意义上的栈,而是与之意思相仿的说法,我们都知道,汉诺塔必须将最上的盘子取走方可移动第二层的盘子,以此类推,不移动上方的盘子,就无法移动下方的盘子,废话不多说,来看看这个代码吧:
def pole_stack():#制造poles的栈
2 poles=[Stack() for i in range(3)]
3 return poles
五、设计移动盘子的代码
准备完前面的工作,现在就要开始移动盘子了,代码如下:
def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-1)*400,150)
plates[mov].goto((tp-1)*400,150)
l=poles[tp].size()#确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-1)*400,-90+20*l)
六、设计操控盘子移动方向的代码
可以移动盘子了当然还不够,只是胡乱地移动无法解决汉诺塔问题,我们要让盘子向着能够解决问题的方向移动,代码如下:
def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= 1:
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-1,withPole,toPole,fromPole)
七、调用
终于完成了全部准备工作,现在就来调用函数,让他们一起发挥作用吧!
import turtle
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)
def drawpole_3():#画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize(10)
t.speed(100)
t.goto(400*(k-1), 100)
t.down()
t.goto(400*(k-1), -100)
t.goto(400*(k-1)-20, -100)
t.goto(400*(k-1)+20, -100)
drawpole_1(0)#画出汉诺塔的poles[0]
drawpole_1(1)#画出汉诺塔的poles[1]
drawpole_1(2)#画出汉诺塔的poles[2]
def creat_plates(n):#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-400,-90+20*i)
plates[i].showturtle()
return plates
def pole_stack():#制造poles的栈
poles=[Stack() for i in range(3)]
return poles
def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
mov=poles[fp].peek()
plates[mov].goto((fp-1)*400,150)
plates[mov].goto((tp-1)*400,150)
l=poles[tp].size()#确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-1)*400,-90+20*l)
def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= 1:
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-1,withPole,toPole,fromPole)
myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()
八 效果