金融工程与并行计算:第一章 并行计算与金融工程的发展 Part 1
本章概要说明整体计算机的发展现况,包括CPU发展的瓶颈,多核技术在绘图卡上的蓬勃发展,金融业使用并行计算的现况,以及平行运算在产品开发上的使用方式。我们也简单回顾市场上GPU的主流开发架构,并以一个简单的例子说明平行运算的效益。最后说明本书的内容架构以及预期达成的目标。
第一节 计算机计算的发展与金融计算的要求
在1965年时,Gordon Earle Moore发表了他著名的摩尔定律,指出同一体积的集成电路(Integrated Circuit, IC)上的组件(主要是晶体管)数目,大约每两年增加一倍。由于IC的计算能力,大体上可以用晶体管的数量来代表,这意味着计算能力只要两年就可以翻倍。也就是说,经过20年下来,IC上的组件数目可以有2的10次方成长,经过40年则可以提高100万倍之多。这提供给我们在计算能力上,大幅度的提升。图一是维基百科上1971年到2011年微处理器上晶体管数量的成长趋势图,大致上也呼应摩尔定律的观点。
现代的财务理论始于1950年代,由Markowitz所提出的投资组合理论(Portfolio Theory),与Treynor、Sharpe、Linter和Mossin进一步的发展所提出的资本资产订价理论(CAPM,Capital Asset Pricing Model),成为财务中研究证券资产价格与风险的数量模型。在这些理论中,基本上是使用随机变量的平均数(Mean)与变异数(Variance)去表达证券的报酬与风险,这种数量上的进展,大幅地提升财务的定量研究。
然而,在1950年代中,还有一个重要的理论发展,对目前财务数量模型有着巨大影响的,那便是由Miller与Modigliani所提出的无套利假说(Arbitriage Free Hypothesis)。此假说主张在均衡的市场情况下,套利组合是不存在的。此一主张对衍生商品的订价模型,有着主导性的角色。
1970年代可说是金融工程的起始时段,这是由于Black、Scholes与Merton(BSM)提出了著名的选择权订价理论(Option Pricing Theory)。事实上,早在1900年便有学者提出了选择订价公式,然而该公式并没有被实务工作者所采用。BSM的模型之所以广为市场所接受,在于其理论假设的合理性,与实务操作上的可行性。BSM应用无套利假说,将选择权与标的股票形成无套利组合,利用此均衡条件,设定此组合的应有报酬为无风险报酬。BSM另一个重要的突破,在于对股票价格行为的假设上,选择了一个相当良好的随机过程(Stochastic Process)─几何布朗运动型式(Geometrical Brownian Motion),配合随机积分(Stochastic Integral)的Ito’s Lemma,得到选择权价格的偏微分方程式。
这些财务理论与实务的进展,都需要大量的数据计算能力。可以这么说,过去40年来的金融创新,也都伴随着计算机计算能力的大幅成长,相辅相成地创造了今日金融产业的蓬勃发展。然而,好景不再,今日摩尔定律似乎也遇到瓶颈,一方面制程技术面临微小结构制造上的困难;另一方面,中央处理器(CPU,Central Processing Unit)的散热问题越来越严重。因此,传统使用单一运算核心(Single Core)之处理器的生产模式,遭遇到严重的挑战。
A. P.Chandrakasan等人在他们的文章“Optimizing Power Using Transformations”(注一)中提出,使用双核心(Dual Cores)的微处理器,可以在相同的计算能力下,减少能量消耗的60%。这一观点促使微处理器转向多核心架构的发展,低频率运行的多核微处理器在功率效能上,有更好的表现。然而,这也给软件产业带来一个全新的挑战,亦即,传统单核的程序撰写模式要转向到多核的程序开发,才能继续享有高速成长的计算机运算能量。
第二节 显示适配器计算能力的跃升
在过去的发展历史上,对于大部分的计算机而言,显示适配器(Display Card)已是个不可获缺的配件。显示适配器的功能一直被定位为辅助CPU来处理计算机上相关图形与影像方面的计算工作。早先显示适配器上的图形处理器(Graphics Processing Unit, GPU)中的运算核心的数目不多,约为2至16个。但近年来,随着制程技术的改良,一方面GPU的运算频率提升,另一方面GPU运算核心的数目大举上升到256至512个。这使得显示适配器每秒所能处理的浮点运算数目跟着明显地提升。
图二(注二)中可以看到,NVIDIA公司所生产的GPU显示适配器,在2003年G80系列之后的单精准度浮点运算的理论值,就开始大幅领先Intel的CPU了,之后逐年扩大领先差距。至于在双精准度浮点运算方面,在NVIDIA推出Tesla系列后,GPU的运算能力也优于CPU的双精准度浮点运算效能。
图二 2001-2014 Intel CPU与NVIDIA GPU理论浮点计算能力
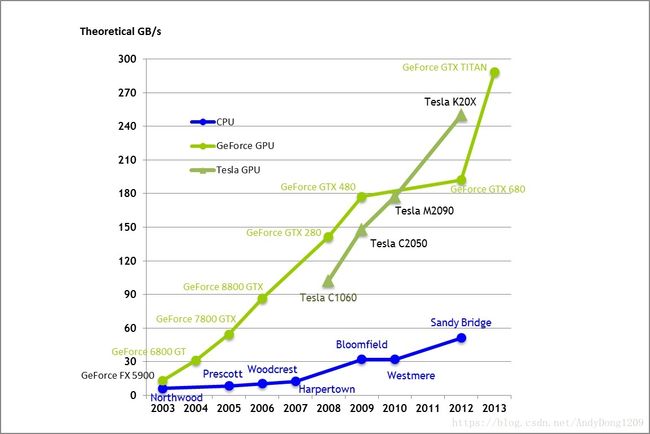
除此之外,显示适配器上的内存容量也达到1至2GB,而且,显示适配器的内存存取带宽也不断在成长。NVIDIA的GeforceGTX 480显示适配器内存存取带宽以达到每秒180GB,明显优于Intel CPU。显示适配器上内存容量的增加以及内存存取带宽的提升,使得涉及大量数据存取的应用,可获得更高的计算效能提升。
图三 2003-2013Intel CPU与NVIDIA GPU理论资料存取带宽
第三节 平行运算与超级计算机在金融界的运用情况
由于前述的理由,根据NVIDIA公司的数据,在2012年Top500超级计算机中,使用GPU (Graphic Processing Unit)以加速运算之计算机以有52台,比重已超过10%。图四(注三)中可以看到在2007~2012中,此一数目呈现快速的增长。
图四 超级计算机使用GPU的成长趋势
另外,在Top50中则有7台超级计算机是以GPU来加速计算。
图五 超级计算机使用GPU的情况
在2013年的Top500超级计算机中,结合CPU与GPU的异质架构已成为市场的主流趋势。在前10名的超级计算机中有两台使用IntelXeon Phi多核协同处理器,包括第一名的中国大陆天河二号,两台使用NVIDIA的GPU来加数运算,包括第十名的中国大陆天河一号A型。
根据牛津大学Mike Giles教授在2013年所做的调查(注四),在所有Top500的超级计算机中,有10%是用于金融计算之上。主要分别用于投资银行与避险基金的业务上。
在投资银行内,计算的重点在于各种选择权订价模型的应用。其中,主要的应用为蒙地卡罗模拟法,占了60%的计算量;PDE与有限差分法次之,约占30%的计算量;其他半解析法最少,约占10%的计算量。这是由于近年来金融产品的创新很多都是将权利条件,加到原有的金融商品之上,也因此产生截然不同的偿付型式。以最近在台湾市场销售的主流结构产品,都是内嵌权利条件的金融商品。至于在避险基金内,则主要使用于高频算法的程序交易之中。
根据NVIDIA的数据(注五),BNP Paribas(法国巴黎银行)使用Tesla GPU进行衍生性金融商品的定价;Bloomberg采用GPU以加速债券定价,J.P.Morgan 的权益衍生性商品部门在 2010 年挑选了 Tesla M2070 GPU 与其全球运算架构结合。另外,各商用软件竞相采用GPU作为计算强化方式,下表摘要专攻计量财务之独立软件开发商(ISV)及采用CUDA的应用程序。
表一:计量财务之独立软件开发商(ISV)及其采用CUDA的应用程序
独立软件供货商(ISV) |
说明 |
Murex |
风险分析(MACS) |
MATLAB® |
数据平行数学 (MATLAB PCT, MDCS) |
Arrayfire |
用于 C, C++, FORTRAN 的 GPU 函式数据库 |
Quantifi Solutions |
资产投资组合风险 (Quantifi Risk), 信用风险 (Quantifi Counterparty Risk) |
Numerical Algorithms Group |
随机数生成器 |
Wolfram Mathematica |
符号运算分析(Mathematica) |
Streambase |
复合事件处理 (Stream Base CEP Engine) |
Risk Management Solutions |
巨灾保险分析 |
Hanweck Associates |
选择权定价(Volera) |
SciComp, Inc |
衍生性商品定价 (Sci Finance) |
Xcelerit |
C++ 专用 GPU SDK,针对 Monte Carlo 和其他数值方法。 |