C-1第二次作业偷鸡的设计思路
1)使用四元组表示a*x**b*sin(x)**c*cos(x)**d
2)在读取上和第三次的版本是一致的
3)在输出上需要判断的逻辑增多
C0迭代开发最终的设计思路
C0-1数据输入处理
1)指导书当中提到两句话表达式式由+-连结多个项组成 ,项由*连接多个因子组成,给出了一种处理数据的方案:
-
首先从头开始提取数据的第一项,紧接着尝试获取一个
+或者-。如果获取到了,说明表达式未结束,便再取一项。 -
如果没有获取到,说明表达式结束。
而对于项而言也是一样。
-
首先获取第一个因子,紧接着尝试获取一个
*。 -
如果获取到了,说明项未结束,便再取一个因子。
-
如果没有获取到,说明项结束。(套娃思路
2)而在表达式当中,符号的出现使得问题变得复杂。
指导书的描述可以这样理解:
-
表达式的第一项可以没有符号 -
项的第一因子可以带符号
那么,只需要对于第一点提到的第一项和第一因子进行符号的处理,就可以完成数据提取。
例如:+++1
-
首先获取第一项,先查看是否有符号,发现是+,记录下来。
-
第一项的获取,首先获取第一因子,先查看是否有符号,发现是+,记录下来
-
最后获取第一因子,发现是+1。
再例如:++1
-
首先获取第一项,先查看是否有符号,发现是+,记录下来。
-
第一项的获取,首先获取第一因子,先查看是否有符号,发现是+,记录下来。
-
最后获取第一因子,发现是1。
3)表达式可以嵌套,指导书提到只有三角函数是允许嵌套内部因子的,表达式因子必须是括号()括起来的
这就给了个思路,在获取因子这一步,先看看是不是括号开头,括号开头说明需要一个表达式,再读一个表达式(这里套娃使用第一点)
读完看看有没有右括号,没有就WF。然后看看是不是sin(或cos(开头,是就获取一下三角函数的内部因子(这里套娃使用第三点)(当然内部可以是一个普普通通的x)
获取到因子最后看看有没有右括号。
4)sin cos exp 还可以有指数,获取完因子后需要尝试读取指数
5)在使用正则表达式进行匹配的时候,使用Patter.compile临时创建一个Pattern会产生不必要的时间和空间浪费,正确的做法是在一开始就编译好各个正则表达式备用
6) 匹配正则的过程当中,需要匹配的种类有很多,使用大量的if else语句并不利于观看,可以使用一个Map储存<种类名(string),模式(pattern)>(注册模式),然后每次只需要从这个map中获取想要的pattern就可以
C0-2 数据的存储格式
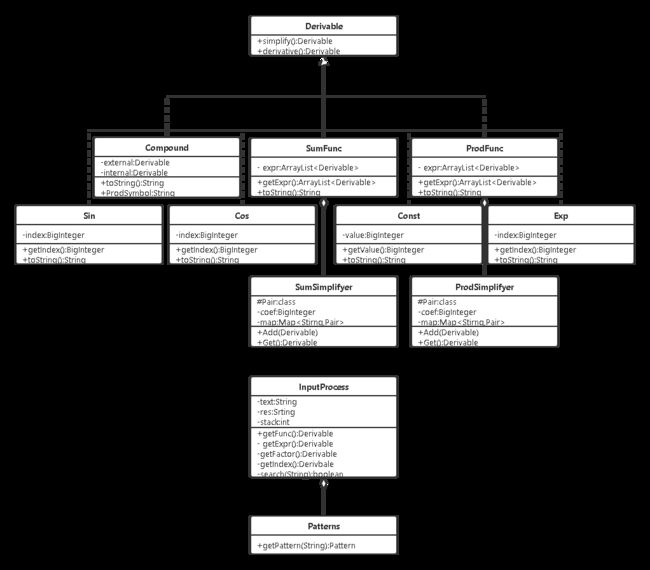
2)所以我使用了普通的多叉树。使用的结点分为两类,一类是简单函数sin cos exp const,一类是指导书提示的复杂类:加法类(内部持有一个函数子结点数组),乘法类(内部持有一个函数子节点数组),嵌套类(由external 和 internal两个函数引用组成)。
3)所有的结点,都实现自一个名为可导函数的接口,都有着同样的成员方法:求导,输出,可能有的简化,整个表达式组织成为一颗树的形式,用户对一个复杂结点(复杂表达式),与对一个简单结点(例如一个因子)的操作是完全一致的,这样就有利于递归地进行处理。(组合模式)
4)这种存储方式,比较占空间,但是对子节点的访问非常方便,所有的子节点都在一个数组里,无论是要进行排序,合并,都变得非常简单。
C0-3 表达式树的简单简化
1)构建一棵树的过程中,很容易出现不必要的结点。比如说(x)+x*(x*x),如果按照上面的方式直接构造,显然,如式子里所体现的,加法类中只有一项,乘法类里面又套了个乘法类。有两种方式去处理这一问题,要么输出的时候写一些代码去规避这些状况,要么在构建的时候规避这些状况。
2)如果输出再去处理,那在一个乘法表达式求导的时候,就需要对它包含一个乘法子元素这个情况来处理。如果构建原时候处理,构建导函数的时候,又得把避免产生冗余结点的这段代码写一遍。干脆就把这段被复用的代码提取出来,成为一个独立的方法,每次构建完或者求导完去调用这个方法完成冗余结点的去除就可以了。
3)具体的简化:
-
对于Sin,Cos,幂函数,如果指数是0,返回1 也就是 sin(x)**0 -> 1
-
对于Const, 直接返回自己就好
-
对于加法节点: 它首先应该更新自己的子节点,把一些不合理的子节点去掉。做法就是接受子节点的返回值,就是调用子节点的简化方法,然后接受返回值,检测到是0就不加进来。 然后它对自身进行简化更新后返回,如果它只包含一个函数,返回这个函数,如果包含子加法节点,应该把子加法节点的元素转到自己身上。
-
对于乘法节点: 同样的,先调用子节点简化方法,接受返回值,检测到1就不加进来。 然后它对自身进行简化更新后返回。如果上一步中又发现自己包含了0,就直接返回0。如果它只包含一个函数,返回这个函数,如果包含子乘法节点,应该把子乘法节点的元素转到自己身上。 也就是说(x) -> x , x+(y) -> x+y, x(yz) -> xyz<\br>
-
对于嵌套类,首先它更新external和internal, 然后对自己更新并返回,如果external是常数,直接返回常数,如果internal是0,那么,sin(0)返回0,cos(0)返回1. 通过层层更新的方式,就可以完成整个树对于冗余节点的去除。 有别的做法是在建立时维护树的结构,不产生冗余节点,但是这么做,所有涉及了创建树的操作, 比如说求导,就都得把这套避免冗余的逻辑一遍又一遍地写,这不是增加了思考难度么。可以看到,我的方法接受一个冗余的树,输出一个标准的树。那么所有涉及到树结构更改的操作,我都不需要考虑这个操作是不是会产生冗余节点,然后写一堆代码规避。我只需要在必要时调用简化方法把它标准化就好了。
对于不同的结点,采取不同的具体策略,但都提供一致的上层接口,这就使得处理能够递归地进行
4)实际上这里还可以同步地进行优化,例如第3点中提到加法结点,就可以先对新子节点数组进行排序,合并同类项后再返回自己本质上是个什么函数。
C0-4 数据的输出
1)每一表达式都由它的项构成,每一项都由它的因子构成
我只简单地提一提自己做输出的时候没有注意到的结点一致性造成的麻烦。
2)我在输出乘法类型和简单类型的时候,会自动补上符号,然后加法类型输出时,只需要将其子结点的各个字符串简单拼接就可以,然后最终输出时,去掉最开始的+。
这样做,加法结点和其余结点的表示就出现了矛盾,一个Sin结点表示成+sin(x),可一个含有Sin结点和0结点的加法结点却表示成sin(x)。
问题出在我把连接加法表达式的各个子项这个任务交给了子节点,实际上,连接操作应该由加法结点自己负责。也就是说,子节点不提供额外的+,让加法结点自己判断是不是要补上即可。
C1 度量分析程序结构
Unit1Task1
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| PowFunc.toString | 5 | 9 | 9 |
-
这个地方不是很懂,输出一个幂函数需要的逻辑就需要这么多,如果拆成指数和系数两部分来输出,可能可以降低复杂度,但是实际上它们功能不是独立的。所以我决定无视这个偏高的复杂度。
Unit1Task2
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Item.toString() | 2 | 21 | 22 |
| Simplifyer.parse(Item) | 5 | 11 | 12 |
-
由于Item是由四元组表示的,所以把一个4元组解释成函数字符串需要多个if-else分支,比较判断4各数的情况。所以复杂度升高。
-
Simplifier的parse方法会讲4元组解析到Map上去,同时对于三角函数需要进行递归合并可合并项,这部分逻辑是比较长。这部分复杂度是难以避免
Unit1Task3
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Compound.simplify | 7 | 3 | 8 |
| InputProcess.getFactor | 11 | 9 | 11 |
| ProdSimplifer.Add(Derivable) | 1 | 9 | 9 |
| ProdSimplifyer.Get() | 4 | 12 | 14 |
-
simplify方法中,由于我使用的Compound由external和internal两个Derivable接口引用来表示,那么实际上没有限制他们具体是什么函数类,但是标准形式下,external只能是三角函数类。所以在化简的时候,使用了大量的if-else语句来对多种复杂情况进行简化
-
getFactor方法是用于获取因子的,由于一个因子可能有多种类型,需要多个if-else分支去尝试获取。同时,它调用了许多类的构造方法来生成因子,所以会导致模块设计复杂度变高。我的想法是使用工厂类来代替生成。
-
ProdSimplifyer中Add方法,由于接受的参数类型可以是任何一种函数类,对于不同的函数类采取不同的策略,所以后面的两个复杂度上升,Get方法也是一样,最初解析到特征Map的那些函数类型是有多种可能的,拿出来也要判断具体是什么类型才能重造,比如说把Sin2*Sin2重造成Sin**4。实际上这是我的存储结构决定了它接受的类型变多,对于每一种类型策略又不一样造成的。可以尝试把带指数三角函数视为嵌套幂函数,这样合并指数会方便一丢丢。但是其它模块可能难受一丢丢。
| class | OCavg | WMC |
|---|---|---|
| ProdSimplifyer | 8.33 | 25 |
| SumSimplifyer | 5.00 | 15 |
-
这两个类都属于简化类,他们使用了所有的函数类,同时,在加法和乘法函数类中会持有这个简化器,所以产生了循环依赖。当初编写的时候是决定这个部分功能相对独立,想拿出来单独思考避免错乱。实际上应该内置到加法和乘法函数类当中的。
C2 Bug分析
1)我在编写一个功能相对独立的方法之后都会进行单元测试,所以有bug也及时解决忘记了。
2)在第二次中测的第一次提交我没有过一个点,是关于指数大小限制的。因为设计的时候不知道还有这个需求。(我觉得是指导书不把要求放一块的锅)
3)在第二次作业,我对树的复杂度控制不恰当,导致树一致无法很好地展开,思考再三我还是选择重构,选择了简单的四元组表示。
4)bug比较容易出现在设计if else分支出现的地方,这个地方需要大量思考,容易出差错。同时也可能出现在隐式的分支,例如DFS算法或者递归算法当中。
C3 测试策略
1)使用批处理程序,对所有成员进行测试。
2)使用手动构造测试样例,前两次作业的表达式复杂度低,还可以接受。但是第三次作业复杂度陡升,导致我没有找到很多bug(就1个)。
3)实际上需要随机测试会更好,随机测试需要考虑边界值测试,避免重复测试,和覆盖性。由于我不会python,所以在比较答案这块吃了亏。
4)我使用的是黑盒测试。因为自己习惯阅读一些成熟的代码所以对于那些面向过程的代码感到无从下手。
C4重构
1)第一次作业使用了工厂类进行对象创建。但是后面两次作业就摸了没有做,因为表达式构建还是比较简单,所以没有去专门设置一个类做这件事情。实际上这是不利于扩展和阅读的。
2)第二次作业一开始是使用表达式树进行构建的,由于考虑不周,出现树的结构严重冗余的情况。为了完成作业选择了非常简单的四元组实现
3)第三次重新使用表达式树,吸取上次的经验,编写了一个简化方法专门用于去除冗余节点。感觉良好。
C5对比与心得体会
1)我可能是实践驱动理论的人,先做一个草案容易发现潜在的问题,为设计做好准备。例如在设计表达式树的时候,几番尝试发现树的结构对几个方法影响很大的,于是在定设计方案的时候提出了标准化树结构的方式。
2)在现阶段,多使用设计模式,不论是否有必要,是有利于理解面向对象思想并且锻炼能力的。
3)节点具有统一接口,统一表达,有利于进行递归处理,减少结点之间的耦合度。
4)将复杂问题层次化处理(比如数据输入),有利于将大的程序分层编写,加速开发, 也有更好的可读性。
5)OOP真的蛮好玩。感觉有兴趣就不会累。不看分就不着急。