OO 第一单元总结

OO 第一单元总结

程序结构分析

由于三次作业都有 100+ 个方法，所以在基于度量的程序结构分析部分，只能把显示警告的方法和总体数据列上。

UML 类图可能较大，可以打开新标签页得到完整图片。

第一次作业

基于度量的程序结构分析

Method	ev(G)	iv(G)	v(G)
com.oocourse.ast.Term.compareTo(Term)	7	3	8
com.oocourse.ast.Expression.toFriendlyString()	5	7	8
com.oocourse.ast.Expression.addTermImpl(List)	4	4	5
com.oocourse.parser.Parser.skipWhitespace()	4	2	5
Total	161	168	208
Average	1.3879310344827587	1.4482758620689655	1.793103448275862

Term 类的比较复杂是因为要比较它们的长度、指数和内容，因此分支较多，导致 ev(G) 较大。Expression 类的两个方法和 Parser 类的方法，也是因为考虑到特判，特殊情况较多，导致 ev(G) 同样较大。

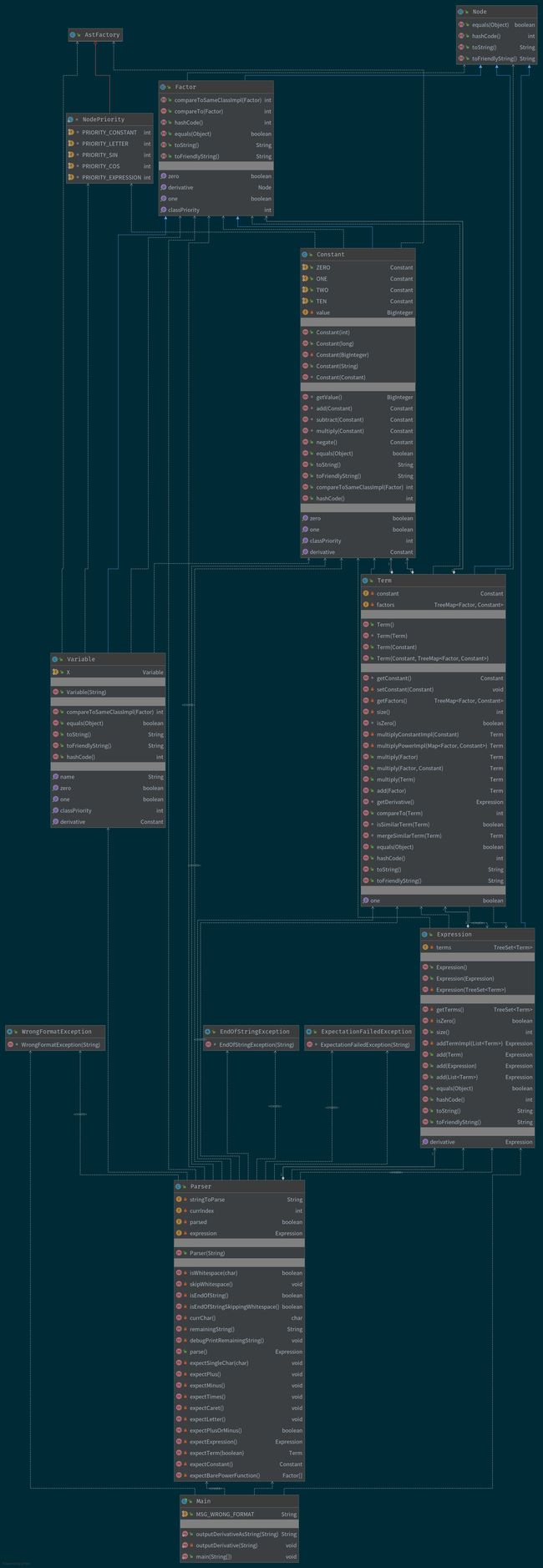
UML 类图

类之间的关系应该相对不算混乱，Term 和 Expression 类承担的职责较重。剩下的类主要用于表达式建模，因此职责较轻。

第二次作业

基于度量的程序结构分析

Method	ev(G)	iv(G)	v(G)
com.oocourse.simplifier.PythagoreanIdentitySearchingSimplifier.simplifyImpl(Expression)	8	5	10
com.oocourse.simplifier.PythagoreanIdentityGreedySimplifier.simplifyImpl(Expression)	5	4	5
com.oocourse.ast.Expression.toFriendlyStringImpl()	5	7	8
com.oocourse.simplifier.PythagoreanIdentitySimplifier.simplifySubexpressionImpl(Expression,Factor)	5	5	5
com.oocourse.ast.Term.compareTo(Term)	5	3	6
com.oocourse.parser.Parser.skipWhitespace()	4	2	5
com.oocourse.ast.Term.toFriendlyStringSinglePowerImpl(Factor,Constant)	4	4	5
com.oocourse.ast.AstFactory.newTrigFunction(TrigFunctionType,Factor)	4	2	4
Total	316	312	387
Average	1.3277310924369747	1.3109243697478992	1.6260504201680672

除了第一次作业提到的比较复杂的方法以外，这次优化器中的方法占了新增复杂方法的绝大部分。搜索优化器的方法较为复杂，是为了节约栈空间，而且怕扔出 Exception 后展开栈造成的时间开销。剩余的方法大体上是化简逻辑本身较为复杂，经过抽象后仍然有比较高的 ev(G)。

UML 类图

类的设计变得较为分散，Term、Factor、Expression 和 AstFactory 类承担的职责较重。实际上可以考虑把表达式管理的机制抽离出来，但是考虑到是数学规律，并没有抽离。

第三次作业

基于度量的程序结构分析

Method	ev(G)	iv(G)	v(G)
com.oocourse.ast.Term.toFriendlyStringPowerTupleImpl(Factor,Constant)	5	5	6
com.oocourse.ast.AstFactory.newTrigFunctionImpl(TrigFunctionType,Factor,Constant)	4	2	4
com.oocourse.ast.Term.multiplyMapOfPowersMutableImpl(Constant[],TreeMap,Map)	4	5	7
com.oocourse.ast.simplifier.BasePythagoreanIdentitySimplifier.simplifySubexpressionSingleImpl(Expression,Factor,Constant)	4	4	4
com.oocourse.ast.simplifier.BaseTwoItemGreedySimplifier.simplifyOnceImpl(Expression)	4	4	4
com.oocourse.ast.Term.multiplySinglePowerMutableImpl(Constant[],TreeMap,Factor,Constant)	4	2	4
com.oocourse.ast.Expression.addSingleTermMutableImpl(TreeSet,Term)	4	5	6
com.oocourse.ast.simplifier.PythagoreanIdentityGreedySimplifier.transformCompatibleTerms(Term,Term)	4	1	4
com.oocourse.ast.Expression.getSanitizedTermsImpl()	4	4	5
Total	389	418	507
Average	1.3460207612456747	1.4463667820069204	1.754325259515571

较为复杂的方法仍然跟第一、二次作业分布类似。由于经过重构，某些功能类似的方法，名字可能有一定改变。ev(G) 较高的，仍然是特殊情况需要较多考虑、逻辑含量较大的内部方法。

由于删去了第二次作业的搜索式化简器，所以对应的方法没有出现。

UML 类图

为了能上传到图床上，图片经过压缩，但是字应该还能看清。

可以看出，Term 和 Expression 这两个类的职责更重了，这是由它们作为表达式树树干节点的功能决定的。同时，优化器依赖的 AstVisitor、创建表达式元素需要的 AstFactory 职责同样比较重。同样没有抽离表达式的基本化简操作。但是优化器部分做的逻辑抽离还是不够，可以考虑重构。

设计思路

输入处理

三次作业都使用上下文无关文法，因此统一使用递归下降法进行输入处理。由于文法不允许有符号整数中符号和数字间有空格，这使得在忽略空格的前提下，写两阶段解析器变得比较麻烦。因此采用一阶段解析器，在 Parser 类中实现。

通过 Parser::expectRuleName 系列方法，实现对文法中规则的检测与解析。如果期望有标记（token）但期望失败，就抛出 ExpectationFailedException。如果检测到一定不符合文法的情况，就抛出 WrongFormatException。

限制指数范围，在文法中规则对应的方法（如 expectPowerFunction）处加钩子即可。

表达式建模

表达式建模成抽象语法树。使用 Node 类表示结点，各个结点所属的类有一定的继承层次关系。

表达式、项、因子、常数、三角函数、字母分别属于 Expression、Term、Factor、Constant、TrigFunction 和 Variable 类。

排序

按照先类别后内容的方式对 Node 排序，可以给 Node 类及其子类的所有实例制定一个全序。因此 Node 类有自然排序，并实现了 Comparable 接口。

数据结构

大体的指导原则是，表达式包括项，项包括常数、因子和因子的指数。

常数是对 BigInteger 的封装，增加了一些实用常量，如 Constant.TWO（在 Java 8 SE 中 BigInteger.TWO 是私有的）、Constant.NEGATIVE_ONE 等。

表达式需要支持合并同类项和按序遍历全部元素，因此选择 TreeSet。项需要支持存储常数，同时考虑到因子的幂次和合并同类项的需要，存储各因子及其幂次的数据结构选择 TreeSet。

对象可变性

Node 类对象全部为不可变对象。因此可以参考 String::hashCode，对它的哈希值和友好表示进行缓存。根据 Java 8 SE 文档，这也满足了 TreeMap 和 TreeSet 对键的要求。

不可变对象也是一种编程范式，或许可以方便 Java 进行优化。

创建

通过 AstFactory 类进行创建，使用工厂模式。Node 类实际上只留下复制构造器，让 AstFactory 负责把调用者的各种参数转换成 Node 类，同时避免引用泄露，从而保持 Node 类的不可变性。

友好表示

友好表示对应 Node::toFriendlyString 方法。

Expression 和 Term 类的友好表示需要特判，尤其是针对表达式中没有项、某一项幂次为 1、某一项本身是表达式这三种情况的时候。

表达式作为因子

第三次作业有一个衔尾蛇式的任务：表达式作为因子。这会带来递归的问题，但在运算中关心的还是无谓的嵌套，如 (((((x)))))。

通过对语法规则和表达式树的分析可以看出，主要要解包两种异常结点：单表达式项（single-expression terms）和单项表达式（single-term expressions）。在 Expression 和 Term 类设好对应的静态方法和对应的解包方法即可。要对涉及 Expression 和 Term 类互操作的方法排查一遍，进行递归式解包。

表达式化简

化简器都是 BaseSimplifier 类的子类，封装化简算法及其相关状态，利用访问者模式实现化简。

功能概述

三次作业中大概实现的化简功能如下。

• 三角函数和差公式
• 勾股恒等式
• 正弦、余弦二倍角公式
• 提取公因子
• 聚合化简
• 不化简（配合聚合化简使用）

主要策略

• 自带的合并同类项和去多余括号。
• 贪心。可以抽象出 BaseOneItemGreedySimplifier 和 BaseTwoItemGreedySimplifier 两个子类，把化简的机制与贪心的策略分离。
• 在利用正弦二倍角公式化简时，把找到的符合条件的 sin 因子按照一定的优先级排列。
• 随机化剪枝搜索。第二次作业中化简勾股恒等式时用到，第三次作业因为时间要求删去。随机化选择策略的范围包括 $ \textstyle{\sin^2(x) + \cos^2(x) = 1} $ 及其两种变形。
• 逐一执行多种策略取最短。

其实并没有特别高级的策略，主要在于广度和技巧性。

随机化也是可以考虑的点，第二次作业中试着实现过。实验表明，随机化剪枝搜索在某些情况下强于贪心。第三次作业性能分较宽松，为求稳并没有用到。

实现

通过 AstVisitor 类来实现较为方便的、对 Node 类内部状态的访问，同时不破坏原来的对象。

各优化器的具体实现，大致基于对表达式结构的理解，实际上与 Node 类的实现多少是耦合的。这是为了性能和易编码性做出的妥协。

评测机

数据生成

通过上下文无关文法的特性进行生成，每个非终端结点通过一定的生成规则生成终端结点。

运行

通过 bash 脚本运行。互测时有些同学使用 JavaFX 的 Pair 类，这时需要使用 Java 8。

SPJ

语法检查采用解析器的黄金模型 ANTLR4。

继承 ANTLR4 生成的语法树访问器，写出转换编译器，可以得到满足 Python 语法的 Python 表达式，再使用 eval 处理。虽然删去前导 0 应该也是正确的方式，但是写转换编译器似乎是一种一劳永逸的方法。同时，也可以在数据检测的过程中方便地加钩子。

采用 sympy 验证答案正确性，第一次作业使用符号化简。后两次作业因为表达式太复杂，使用可控制精度的数值计算。

测试驱动开发

每次改动（尤其是大改）时，自动评测防止退化。

设计模式

第一次作业由于对象创建的情况比较少，并没有使用对象创建相关的设计模式。第二次作业以后，在 AstFactory 类中使用了简单工厂模式。

实际上，在一些实用类中，仍然可以把这个类改成单例模式。这样方便使用该类，也方便状态的共享。

在化简时，其实也可以对 AstFactory 类所涉及的功能进行改造，采取抽象工厂模式的策略，来规范表达式相关对象的创建。

杂项

I/O 抽象

把调试信息放入单独的缓存中，等到真正的结果输出后，再作为调试信息输出。

复杂度分析辅助开发

尽量降低复杂度较高的方法，简化逻辑，通过这种方式发现 bug。

公测和互测情况

第一次作业

强测 100，刀不到别人，别人也刀不中自己。

第二次作业

因为搜索化简器的时间没有控制好，导致一个点超时。同样是刀不到别人，别人也刀不中自己。

第三次作业

被找出 2 个 bug。一个是 TrigFunction 类中 sin(x**2) 不能输出成 sin(x*x)，这和 Term 类的要求不一样。因此强测中 5/20 个点输出格式错误，得到 75 分。别人刀中自己 7 刀，6 刀是因为这个 bug。另一个是因为在 Term 中，幂次高于 1 的表达式因子，要输出成连乘的形式，否则格式错误。

经验教训

3 个 bug 暴露了测试阶段的问题。过度迷信随机测试和黑盒测试，导致边界情况难以被考虑。

刀人策略

发现 bug 主要采取三方面措施。

• 自己构造样例进行评测。这种方式能够感知到常见错误，但是对每个人的实现细节缺乏考虑。
• 针对源代码进行评测。这种方式可以和其它方式结合起来，更有针对性。
• 随机评测。效率最低，但是可以发现隐藏的 bug。

总结与反思

第一单元是理解什么叫做面向对象的一个单元。在面向对象中，工程性变得尤为重要，因此架构的重要性也是比较明显的。在高效地构建的同时，也要高效地防止破坏。有效的测试就是对应的手段。

对比和心得体会

通过阅读大佬们的程序和优秀代码，深切地感受到架构和测试的重要性。如果重构和防退化带来的开销大于优化带来的好处，那么不如放弃赌博式的优化。

同时，还有避免过度设计。事实上三次作业都可以用正则解决，使用递归下降有理论严密性的保证和重构的方便性，但是略微有点臃肿。command 包的设计则完全没有必要，因为发号施令的只是 Main 类，改变具体操作的开销较小。这是一种典型的过度设计。

展望

架构改进

对象层次结构

似乎可以统一 Expression 与 Term 类，这样就不需要对单表达式项和单项表达式进行处理了。

扬弃 TreeMap 和 TreeSet 的结构，只在加减项时使用。为了效率，可以使用 Term[] 和 PowerTuple[]，在插入数据的时候可以进行二分查找或利用 TreeMap/TreeSet。

使用对象池模式，借鉴 String::intern，使得同样的参数生成同样的引用这种情况发生的概率尽量大。

比较

比较时可以使用 Comparator#comparing、Comparator#thenComparing 和 Integer#compare 等方法。

在类中把比较器作为常量封装，把比较的策略抽离出来。

Node::equals 中使用 Node::hashCode 来粗略地判断是否相等。

化简

处理勾股恒等式时，可以先对 sin 降次，再对 cos 降次，提高化简效率。

对 Expression 的匹配，可以借鉴 Pattern 类实现 Formula 类，从而使化简器真正不需要了解 Node 类及其子类的实现细节。但是一旦有歧义，复杂度难以控制。

用更多更好的方式超越贪心。

测试

提升测试强度和代码覆盖率。

提升 sympy 执行速度或换掉 sympy。试过 Pypy 3.6，然而 sympy 对 Pypy 这种追踪型 JIT 解释器很不友好。而且 Pypy 在处理 CPython 的扩展库时有额外性能开销。因此总体性能反倒比 CPython 慢。或许可以试试 MATLAB 或 Mathematica 这种更接近本地的计算机数学软件。

并行测试，无论是通过多线程还是多进程实现。

杂项

写一个统一的 .gitignore，现在的太乱了。

尝试使用 IDEA 的 Markdown 支持，Typora 的等宽字体在 zh_CN 的 locale 下是坏的。