经过三次OO作业之后,OO作业的第一单元功能部分告一段落。在这几次作业的完成过程中有了一定的收获。
一、第一次作业
1.架构分析
本次作业需要完成的任务是简单多项式函数导数的求解。表达式仅仅支持简单的幂函数项的加减法运算,同时输入保证规范性,即不会出现错误类型的数据。整体要求上比较初步,实现起来也较为简单。但由于初步设计(之前也有设计过但是时间久了没印象了)面向对象思想的程序,很多知识较为生疏,因此代码的设计思想还是类似面向过程的,而且代码的可扩展性也很差,这导致了我后续作业过程中遇到的问题。
设计过程中大概用到的思路是对表达式做一定的处理,通过项之间的连接符号(使用了'+')分割了不同的项,对每个项通过一个统一的幂函数求导法则求导出结果,对其中某些结果进行特判以优化结果后得到输出。考虑到这次作业并没有格式错误的问题,此次作业的表达式格式判断中并没有引入正则表达式。
2.性能分析
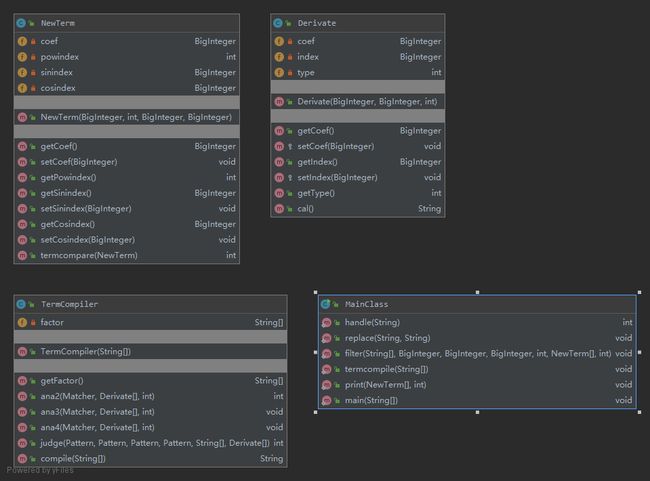
这次作业的类图如下图所示:
从这个类图中可以看出,类之间并没有明显的关系,每个类只是执行了各自的功能,并没有特别实质的联系。
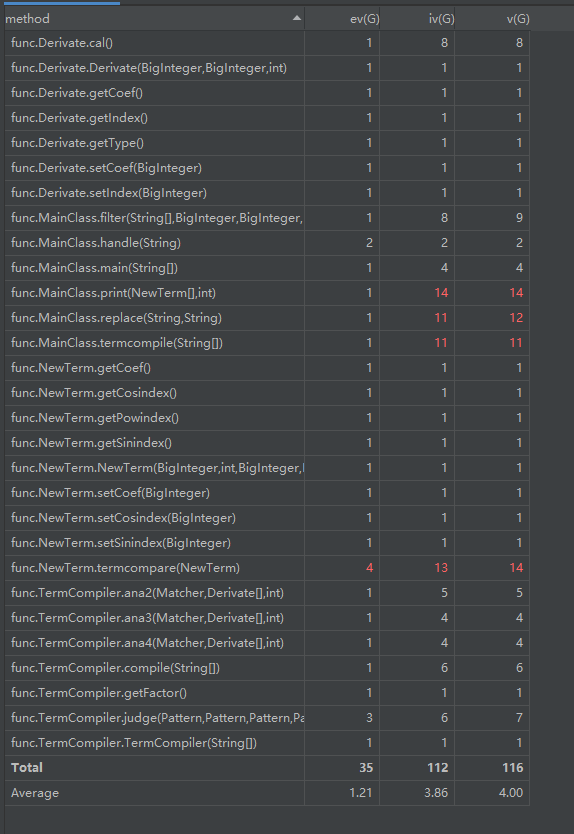
复杂度分析如下:
ev,iv,v分别代表了不同的复杂度。
-
ev(G)基本复杂度是用来衡量程序非结构化程度的,非结构成分降低了程序的质量,增加了代码的维护难度,使程序难于理解。
因此,基本复杂度高意味着非结构化程度高,难以模块化和维护。实际上,消除了一个错误有时会引起其他的错误。
-
Iv(G)模块设计复杂度是用来衡量模块判定结构,即模块和其他模块的调用关系。
软件模块设计复杂度高意味模块耦合度高,这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度,因此模块设计复杂度不能大于圈复杂度,通常是远小于圈复杂度。
-
v(G)是用来衡量一个模块判定结构的复杂程度,数量上表现为独立路径的条数,即合理的预防错误所需测试的最少路径条数,圈复杂度大说明程序代码可能质量低且难于测试和维护。
经验表明,程序的可能错误和高的圈复杂度有着很大关系。
可以看出resultprint和term_imple两个方法的复杂度较高,resultprint方法中使用了较多的特判对输出结果进行判定,term_imple方法中对于输入表达式的修改也有较多操作。这可能是导致程序出现复杂度的原因。
3.Bug分析
这次作业在中强测过程中未发现bug,在互测过程中也没有出现bug,同时测试的过程中发现了组内成员的两处bug。同时这次测试过程中,我没有阅读组内成员的代码,仅仅是测试了几组自己编写过程中遇到的问题样例,例如通过由于项的加减导致结果为零的样例,因此此次测试只发现了同组人的两处bug。
二、第二次作业
1.架构分析
本次作业需要完成的任务加入了对于简单三角函数的求导,以及对于错误形式的判断。其中三角函数的形式只能是sin(x)或cos(x)。错误形式涉及特殊符号,不合法因子,不合法字符,幂函数指数等等内容。
由于涉及到表达式合法性的判断,这次作业我构建了一个基于所给的表达式构架法则的正则表达式树状结构,通过这个结构判断输入表达式的合法性。同时在通过形式判断正确性后,在处理的过程中获取幂函数指数,比较其绝对值与10000的大小,完成指数合法性的判断。(这一部分也是强测过程中出现bug的主要来源之一)
2.性能分析
这次作业的类图如下图所示:
这次作业我考虑到将求导的不同部分,例如分离项,处理项,对项进行求导,整合等等功能分成不同的类进行处理。但是由于我没有考虑未来作业中函数可能嵌套的问题。所以设计的程序还是缺乏拓展性,这对我下一次作业设计也造成了不小的麻烦。
复杂度分析如下:
从复杂度分析可以看出,由于对表达式不同情况的特判过多,对于输入表达式项的处理以及加工依然存在很高的复杂度,这也是我这次作业被hack的主要问题点之一。
3.Bug分析
这次作业在中测过程中未出现问题,但是由于遇到某些特殊符号时未作处理的问题,在强测过程中我有几组样例产生了异常,这一问题在互测过程中也被hack到了几次。在互测过程中测试的几组样例没有发现组内成员的bug。
三、第三次作业
第三次作业在第二次作业的基础上,加入了幂函数的嵌套功能,即在第二次作业的基础上,加入因子表达式这一定义,并且在三角函数的定义中引入这一元素,即三角函数的括号内可以加入因子表达式,同时对于幂函数的指数增加了新的限制。这一引入极大地增加了设计过程中的难度。我最初的想法是继承第二次作业的正则表达式判断,对于三角函数括号内的因子表达式做替换,同时将嵌套处理成一种新的运算方法。例如sin(x**2)处理为sin(x**2)@x**2,同时对@之后的成分进一步嵌套分析,直到@后的因子不再包含括号。我认为这一操作是可行的,同时也能够合理获取表达式中的各个项成分。但是由于一些特殊情况(一些个人原因)导致看到这次作业的时候距离提交的ddl已经痕近了,给我处理程序问题的时间很紧促,因此我没能完成这一次作业的功能代码,设计出的代码也没能通过中测。
四、心得体会
这一单元需要我们完成的主要功能是对于多项式的求导,以及对于幂函数嵌套,三角函数嵌套等等功能的处理。
在这一单元的设计过程中,由于面向对象程序设计思想的不完善,我程序的设计思想还是不够合适。面向对象这一设计思想的体现也不够明显。同时这三次作业的处理过程中都是用静态数组完成的数据存储。用同学的话来说,这不OO。但是这三次作业确确实实地让我在面向对象的程序设计能力上有了较大的提升。同时对于java这一程序语言的功能模块也有了更深的理解和熟悉度。OO这门课还是难度很高的一门课,同时课程的时间安排也很紧凑,这要求我们在程序设计方面多下功夫多思考。从这一角度来说,它是对编程能力的一个很大的提升。在今后的学习过程中,我应该付出更多的努力。
同时,在这次设计过程中,我遇到了很多无法同时兼顾性能优劣与程序性能分的问题,对于程序输出结果的优化会导致程序的性能下降,这是一个不好平衡的问题,如何优化算法,在今后的设计过程中平衡好程序的性能的同时,获得更多的性能分,也是需要我思考的方向。