爬山算法
在介绍这两种算法前,先介绍一下爬山算法。
爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
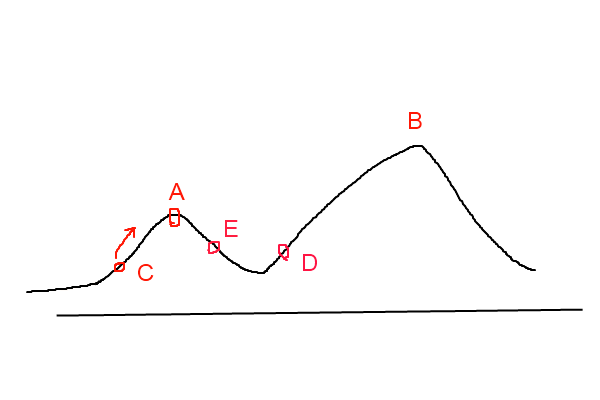
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如图1所示:假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。
模拟退火算法(SA)
为了解决局部最优解问题, 1983年,Kirkpatrick等提出了模拟退火算法(SA)能有效的解决局部最优解问题。模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。
算法介绍
我们知道在分子和原子的世界中,能量越大,意味着分子和原子越不稳定,当能量越低时,原子越稳定。
“退火”是物理学术语,指对物体加温在冷却的过程。模拟退火算法来源于晶体冷却的过程,如果固体不处于最低能量状态,给固体加热再冷却,随着温度缓慢下降,固体中的原子按照一定形状排列,形成高密度、低能量的有规则晶体,对应于算法中的全局最优解。
而如果温度下降过快,可能导致原子缺少足够的时间排列成晶体的结构,结果产生了具有较高能量的非晶体,这就是局部最优解。
因此就可以根据退火的过程,给其在增加一点能量,然后在冷却,如果增加能量,跳出了局部最优解,这本次退火就是成功的。
算法原理
模拟退火算法包含两个部分即Metropolis算法和退火过程。Metropolis算法就是如何在局部最优解的情况下让其跳出来,是退火的基础。1953年Metropolis提出重要性采样方法,即以概率来接受新状态,而不是使用完全确定的规则,称为Metropolis准则。
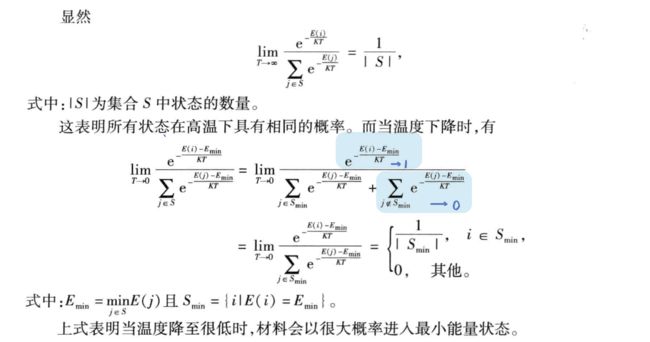
状态转换规则
温度很低时,材料以很大概率进入最小能量状态
模拟退火寻优方法
注意事项
- 理论上,降温过程要足够缓慢,使得在每一温度下达到热平衡。如果降温速度过缓,所得到解的性能会较为令人满意,但是算法太慢会导致较搜索算法不具备优势。
- 要确定在每一温度下状态转换的结束规则。实际操作可以考虑当连续m次的转换过程没有使状态发生变化时结束该温度下的状态转换。
- 选择初始温度和确定某个可行解的邻域的方法也要恰当。
算法流程
-
初始化
- 初始温度T
- 初始解状态\(S_0\)(算法迭代的起点)
-
在可行解的邻域内产生新解\(S'\),并判断该新解是否可以被接受。当连续\(m\)次的转换过程没有使状态发生变化时结束该温度下的状态转换。
-
判断是否满足终止温度,如果满足输出当前解作为最优解,否则降低温度。
- 最简单的下降方式是取定一降温系数\(\alpha<1\),以\(T_{n+1} = \alpha T_{n}\)的形式下降,比如取\(\alpha=0.99\),一般取值为0.8到0.99之间;
- 其他温度下降方式有:\(T_n = \frac{T_0}{log(1+n)}\)、\(T_n = \frac{T_0}{1+n}\)
遗传算法(GA)
算法介绍
初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。
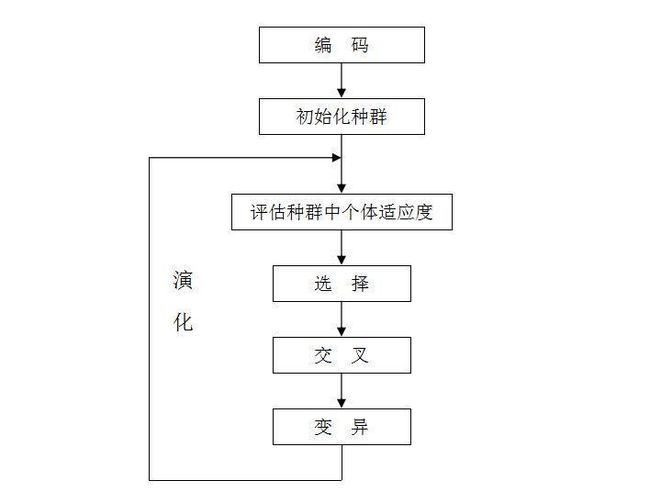
遗传算法的流程
- 随机产生种群。
- 根据策略判断个体的适应度,是否符合优化准则,若符合,输出最佳个体及其最优解,结束。否则,进行下一步。
- 依据适应度选择父母,适应度高的个体被选中的概率高,适应度低的个体被淘汰。
- 用父母的染色体按照一定的方法进行交叉,生成子代。
- 对子代染色体进行变异。
算法实现
编码
仅对浮点编码法进行介绍。
个体的每个基因值用某一范围内的一个浮点数来表示。在浮点数编码方法中,必须保证基因值在给定的区间限制范围内,遗传算法中所使用的交叉、变异等遗传算子也必须保证其运算结果所产生的新个体的基因值也在这个区间限制范围内。
比如一个9目标问题的一个染色体为:
[0.23, 0.82, 0.45, 0.74, 0.87, 0.11, 0.56, 0.69, 0.78], 区间范围限制为[0,1]
初始化种群
自行用某种算法得到一个较好的初始种群。
设定适应度函数
用于区分群体中个体好坏的标准。
设置选择函数
对群体中的所有个体按适应度大小进行排序,基于这个排序来分配各个个体被选中的概率。
单点交叉
变异操作
按照给定的变异率,对选定变异的个体,随机地进行变异。可随机取三个整数\(u,v,w\),把\(u,v\)之间的基因段插到\(w\)后面。
参考网站与书籍
[1]【算法】超详细的遗传算法(Genetic Algorithm)解析https://www.jianshu.com/p/ae5157c26af9
[2] 深度学习 --- 模拟退火算法详解(Simulated Annealing, SAhttps://blog.csdn.net/weixin_42398658/article/details/84031235
[3] 数学建模算法与应用,司守奎,孙兆亮