UnitOneSummary
目录
- 一、程序结构分析
- 第一次作业
- 第二次作业
- 第三次作业
- 二、Test & Bugs
- 三、设计模式
- 四、总结与反思
一、程序结构分析
第一次作业
思路:
1.输入预处理:
- 去除空格和\t
- 替换++、--、+-、-+
- 将+x,-x,x+,x-替换成+1*x,-1*x,x**1+,x**1-。至此已将输入中的每一项全部替换成[+-]\d+*x**[+-]?\d+
- 最后用正则提取每一项
2.合并化简求导
HashMap
3.关于格式化输出
因为系数和指数都是整数,所以求导之后只有指数是-2的项需要考虑系数是否为1或-1
求导之后指数是0,直接输出系数;指数是1,如果系数还是1或-1,那么求导之前项的系数只能是分数,如果只按指数讨论,笔者的格式化输出逻辑减少5-6行,当然你也可以像第一次实验的输出要求一样讨论
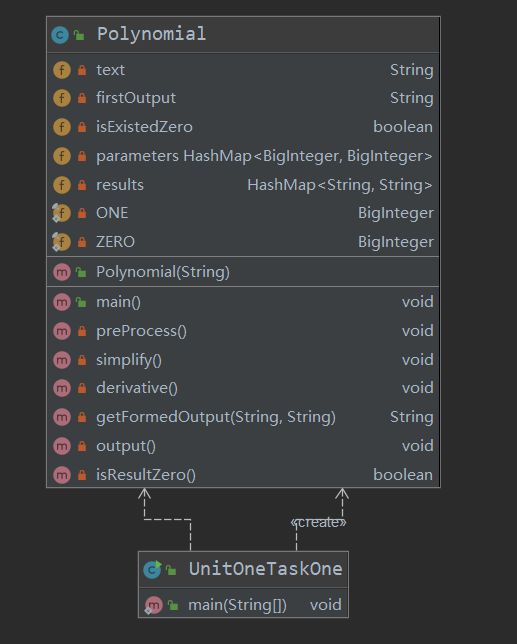
UML:
LinesCounter:第一次代码总行数128
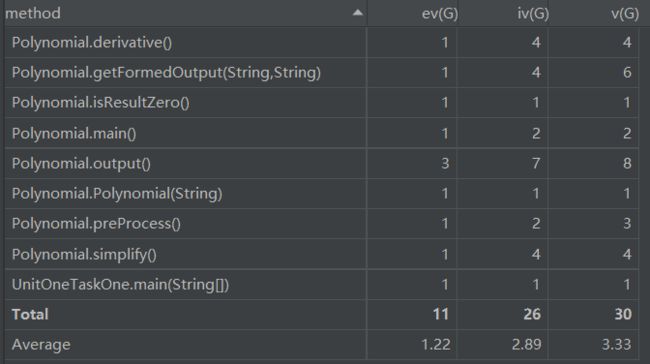
Metrics:第一次作业尚未飘红
第二次作业
思路:
1.判断表达式合法
- 去除空格和\t
- 判断是否为空串
- 以项为单位构造正则,逐项匹配
2.合并因子并求导:
构建求导的抽象类,每种函数继承抽象类,方便合并因子及求导
3.化简:
合并同类项:
对于x,sin,cos的指数相同的两项,合并系数:重写了hashcode和equal方法,把x,sin,cos的指数当成三元组,把三元组当成Hashmap的key,系数当成Hashmap的value,通过判断是否containkey,进行同类项的合并
分类:
按照x的指数分类,将系数,sin的指数,cos的指数当成三元组
对于指数不同的项无需考虑三角函数的化简
对于每个x的指数对应的若干三元组深搜剪枝化简:
设sin指数为m,cos指数为n,则对于①(m,n) ②(m,n+2) ③(m+2,n)
①②③任选两者的组合都可以转换成另选两组的组合。为方便讨论,设两项的公共部分为F,详细讨论如下:
①+② <--> ①+③:a*F+b*F*cos(x)**2 <--> (a+b)*F-b*F*sin(x)**2
②+③ <--> ①+②:a*F*sin(x)**2+b*F*cos(x)**2 <--> a*F+(b-a)*F*cos(x)**2
①+③ <--> ②+③:a*F*sin(x)**2+b*F <--> (a+b)*F*sin(x)**2+b*F*cos(x)**2
类似转换方式还有:
a*F*cos(x)**2+b*F <--> -a*F*sin(x)**2+(a+b)*F
a*F*cos(x)**2+b*F*sin(x)**2 <--> a*F+(b-a)*F*sin(x)**2
a*F+b*F*sin(x)**2 <--> a*F*cos(x)**2+(a+b)*F*sin(x)**2
利用可能使结果长度缩短的以上转换,进行深搜剪枝化简
深搜:
标记+回溯,对于每个没有被访问的三元组,尝试按照6种转化形式变换,递归到底之后判断总长度是否减小
剪枝:
采用贪心的思想,每次转换同时将转换之前的项设置成对照,如果未能使长度减小,直接return
熔断:
根据第二次评测机2s限定的CPU时间,设定深搜部分的时间阈值1000ms,即超过1000ms之后直接throw exception
4.格式化输出:
重写toString
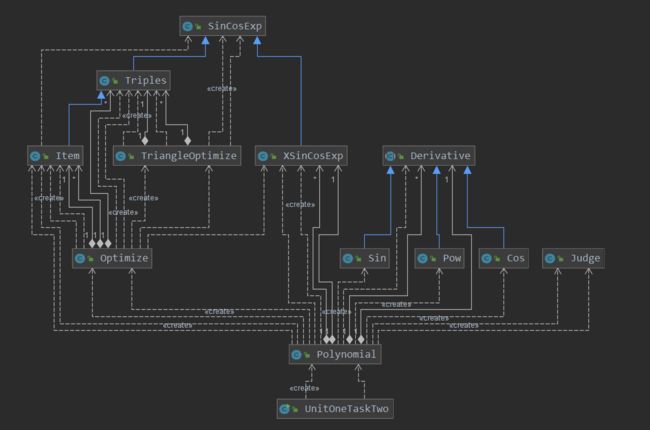
类之间的逻辑和调用关系:
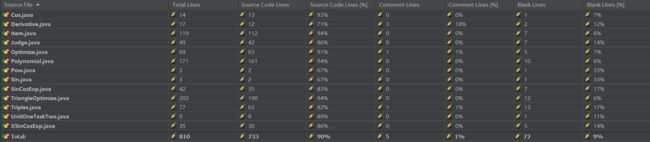
LinesCounter:第二次代码总行数733
Metrics:化简部分的复杂度较高
第三次作业
思路:
1.判断表达式合法:
- 排除空串(只有空格和\t的也算作空串)
- 排除非法字符
- 排除空格引发WF的情况
- 排除非法阶乘
- 排除非法三角函数
- 排除非法数字
- 去掉空格和制表符
- 排除非法加法减法符号
- 排除非法指数和底数
- 排除不匹配的括号
2.求导:
只对表达式因子和嵌套类的三角函数建树处理,其余正常处理。建树时按照优先级嵌套>乘法>加法=减法,设置权重,方便建树
3.化简:
求导结果只有*,+,-,所以递归化简,去除多余的0,1,括号
4.格式化输出:
重写toString
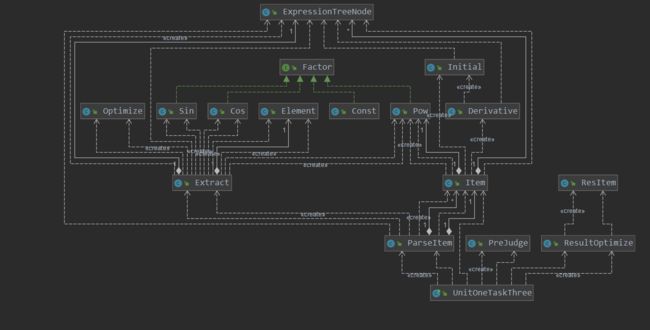
类之间的逻辑和调用关系:
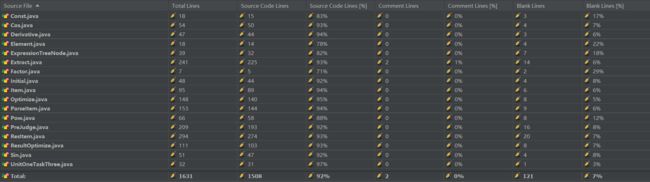
LinesCounter:第三次作业总行数1508
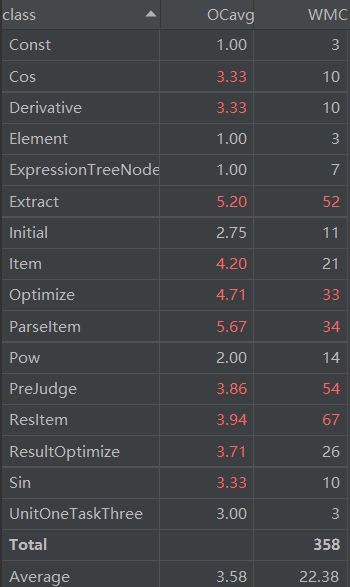
Metrics:由于循环和判断逻辑较多,所以大面积飘红
二、Test & Bugs
Test:
在第一次作业强测之前已搭建好评测机,三次作业使用只需改变生成数据的正则
思路:
- 1.用xeger根据自己设计的正则表达式批量生成测试数据的文件input.txt
- 2.然后将input.txt逐行作为输入 ,运行.class 获得输出文件tmpOutput.txt
- 3.然后对tmpOutput.txt的内容采用sympy进行表达式求值(比如代入x=2),获得输出文件myOutput.txt
- 4.用sympy包对input.txt的内容逐行求导并进行表达式求值,令x=2,获得输出文件correctOutput.txt
- 5.比较myOutput.txt和correctOutput.txt,如果存在不同,根据行数查找input.txt的测试数据
按照1-5的逻辑编写.sh ,bash运行完成黑盒测试
具体细节处理:
1.1去除生成数据的前导0
#去除前导0
str = re.sub(r'(?1.2 代入2计算
result = int(expr.evalf(subs={x: 2}))
1.3 使用管道,简化sh编写
cat $InputFileName | while read line
do
...
correctOutput=$(echo "$line" | python diff.py)
result=$(echo "$myOutPut$space$correctOutput" | python compare.py)
...
done
另一种测试方法:Junit
//本次主要使用sh
import org.junit.Test;
import JUnitTestTools.EnhancedUserTestTools;
import java.io.File;
public class PolyTest {
@Test
public void main() throws Exception {
new EnhancedUserTestTools(Poly.class, 2000).testAll(new File("./test/poly/test1.txt"));
}
}
Bugs
强测:
三次强测均未测出bug
hacked:
三次互测均未被hack
hack:
三次互测平均每次hack非同质bug2个,其中主要是输出时toString的逻辑和细节处理,以及第三次作业存在的优化过度的问题。
三、设计模式
主要采用工厂模式。
第一次作业由于仅用128行实现,没有考虑向后兼容性,所以没有设计工厂(之后单元应该着重注意代码向后兼容的能力)
第二次作业考虑了向后兼容性,设计了抽象类,sin,cos,pow,const均继承抽象类,搭建工厂
第三次作业在第二次作业的基础上,实现递归逻辑。配合树结构的使用,保证了正确性
四、总结与反思
三次作业主要锻炼了各个容器的使用,工厂模式的应用,优化方式的探索。虽然三次作业的完成都保证了正确性,但尚有很多不足。比如第三次作业中采用二叉树的结构,①是给后续的化简带来极大的困难,②是树结构与业务逻辑紧密绑定,可能无法满足后续的扩展要求。但是如果设计一个统一的item接口,然后不仅让sin,cos,pow,const实现这个接口,而且让各个组合项+,-,*,嵌套也实现这个接口,只需要组合项是内置两个item一个operator,不仅方便化简,而且无需采用树结构,简化代码逻辑,同时能保证向后兼容性,无论之后出现新的因子,还是新的组合模式,只要实例接口即可。
相比于正确实现功能,个人认为优化部分更具有挑战性,尤其是在优化的同时,保证正确性,而不是因为20分失去应得的80分。比如在第二次作业中,采用了dfs深搜的优化方式,但可能会出现TLE的问题,所以要设置熔断。在第三次作业中,如果采用二叉树,可能面临无从化简的处境。