原题链接
程序在文末
1.分析输入数据
输入的地图的大小在 1 ~ 20,规模小,如果用dfs或bfs,并且每个点最多访问一次,则最多访问 400 个点
推测dfs和bfs访问一个点的过程中需要调用其他复杂函数,如此一来时间消耗才合理,因为单纯访问400个
点20次(leetcode的测试用例一般在20左右)可能连1ms都用不到,通常来说一道题耗时 > 1ms
2.分析题目类型
游戏题目,和地图相关,和图结构相关,而且和路径搜索相关,很自然联想到 bfs 或 dfs
但是不能只对玩家或者箱子使用bfs或dfs,因为要求人推着箱子,把箱子推到目的地,人和箱子都是要动的。
所以要把人和箱子的状态结合起来使用bfs或dfs,于是有解决方案1 : bfs + 优先队列(存状态)。
下文的状态几乎都是指(人的位置 与 箱子的位置)
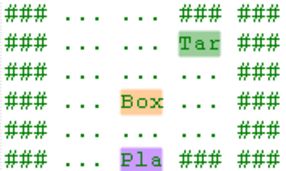
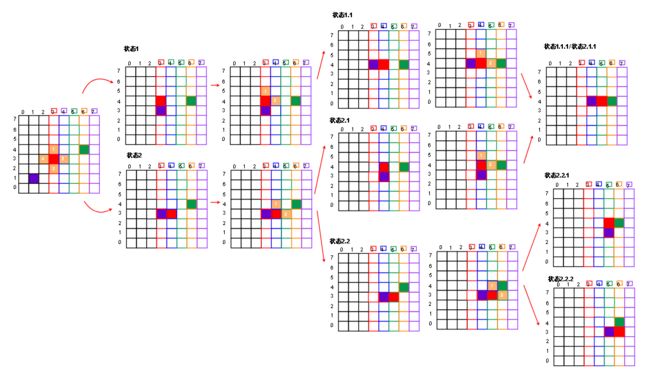
以下图为例,紫色代表玩家,橙色代表箱子,绿色代表箱子最后要到达的位置(Target),### 表示墙壁, ... 代表可走位置
首先要解释优先队列以什么优先,本题要做的是求箱子推到Target位置的最短推动次数,也就是箱子移动的距离,所以bfs以箱子移动到Target位置的曼哈顿距离为优先级(距离优先bfs)
每次都先考虑箱子离Target最近的状态的话,那么最后箱子移动的次数是最少的,而这里度量 “近” 的标准是 “曼哈顿距离”。
其实很简单,就是起始点和终点的 垂直距离绝对值 + 铅垂距离绝对值,起始点是箱子位置,终点是Target位置,于是当前状态(包含箱子和人的状态)的优先级 = 1 + 2
为什么曼哈顿距离小,就表明箱子离Target近?
因为只能上下左右移动,不能像上图这样直接穿过去,如果可以的话可以直接使用初中教的欧式距离(distance = (dx ^ 2 + dy ^ 2) ^ (1/2))
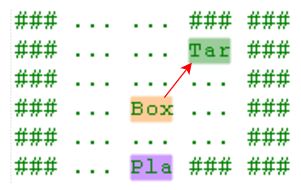
按BFS的走法,上图能走到以下两种状态,两种状态的箱子到Target的曼哈顿距离相同,所以优先级一样。
如果把这两种状态放到优先队列里,则下一次pop出来的是两者任一(确切地说应该是先进去的那个)
两种状态接着向下走,状态2.3和状态1.1相同,舍弃。而且要记得不能往回走,也就是状态1.1不能走回状态1,所以在程序中需要一个数据结构标记已经走过哪些状态
状态1.1,2.2,箱子离Target的曼哈顿距离一样,且都大于2.4的曼哈顿距离
所以,2.4优先被选中,依此状态接着走,到2.4.2忽略掉中间过程,箱子不动玩家动的几个状态。
得到上面这两个状态,答案就清晰明了了,因为两个状态最后都能把箱子推到Target,两者推动箱子的次数一样,且都是最少次数,也即箱子最少移动步数。
只要箱子推到Target就返回,所以优先级比较低的1.1和2.2没有继续走下去,减少了执行次数。就算高优先级的状态最后走不通也无所谓,因为还有低优先级的走法存在,如果所有低优先级的走法
都不能让人推着箱子到Target,那确实走不通。
上面的想法看似不错,但还不够,问题在于,题目只关注箱子移动的最少次数,重点在箱子,而我们目前是把目光聚集在人上,让人带动着箱子动。这样的话,在人还没贴近箱子的情况下,也就是
除了状态2.4,2.41,2.42 外,其他状态都是在像无头苍蝇一样到处乱撞,因为优先级都一样,这样的话就添加了很多无所谓的状态。
如何减少这些无关紧要的状态?
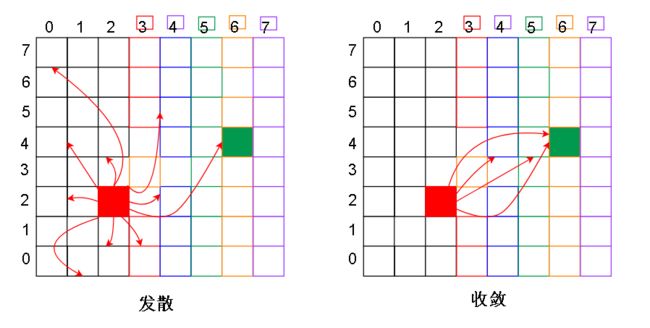
我们把目光放到箱子上,而不是人上。因为想要得到的是箱子到Target的最短距离,所以应该以箱子为重点,找箱子到Target距离最短的路径,再让人到达能推箱子的位置
怎么找到箱子到Target的最短路径?A*寻路可以帮我们解决问题,A* 的优先级函数 f = g + h . 其中 g为箱子已经移动的次数,h 为当前状态的箱子到Target的曼哈顿距离
把箱子的起始点放入优先队列,每次都取优先队列中优先级函数值最小的点(访问该点),并且把这个点周围未访问的点加上优先级后入队,直到访问到Target
放入优先队列的其实不只是箱子的位置,还要带上人的位置,(把 人的位置 + 箱子的位置 称为状态),因为需要知道人能不能到达某个位置去推现在的箱子,让箱子到某个位置上
当然,为了保证步数最少,并且减少运算次数,需要记录每个状态的箱子移动步数。如果当前访问状态步数 大于等于已经记录过的步数,则直接跳过当前状态
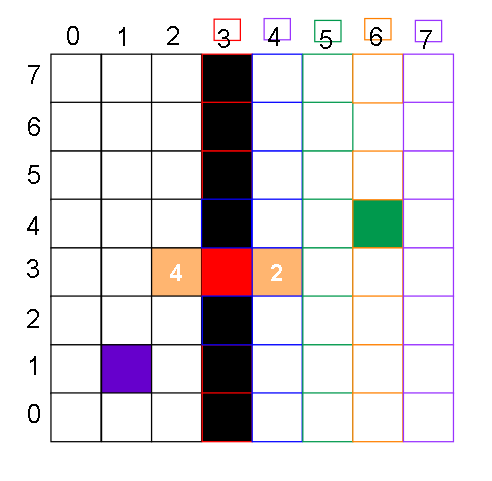
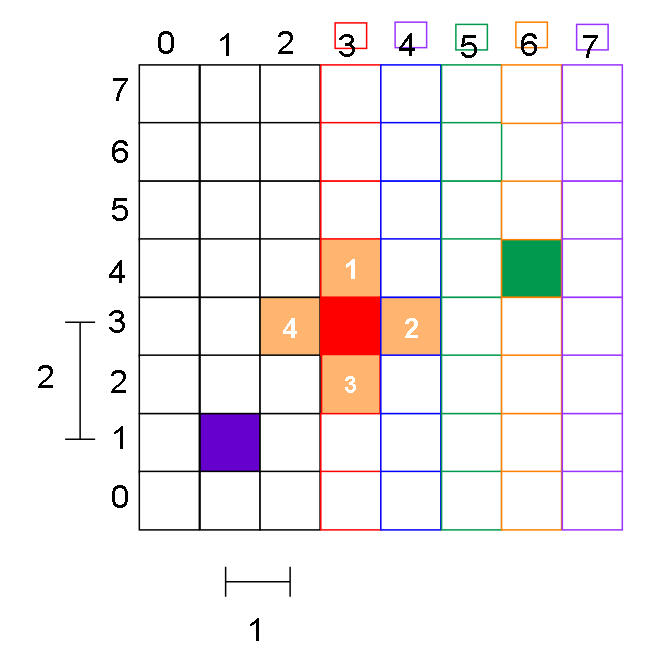
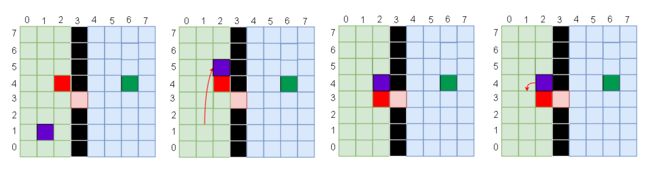
一个例子:
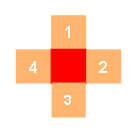
紫色 = 人,绿色 = Target 终点,红色 = 箱子,橙色方块代表箱子bfs可能选择的位置,上面的数字表示bfs的延伸顺序
其实每个状态的箱子都有4个方向可以走,但是只有方向1和方向2能更接近Target,所以无视3,4,只有1,2走不通才考虑3,4
同理,没有表现状态1往方向1移动后的状态,因为虽然箱子往方向1移动和往方向2的移动步数(累积)相同,但是方向1的位置与Target终点的曼哈顿距离大于方向2的位置
只有往方向2走不通才考虑方向1
我看过一种写法是用 Map 来保存状态和移动步数的,如果已经记录的当前状态的移动步数小于等于 父状态移动步数 + 1,就直接返回,否则则把当前状态的步数更新为新的最小值
这是一种类似迪杰斯特拉的写法,但是要知道 A* 已经是自带迪杰斯特拉的了。而且笔者试了这种用 Map 保存移动步数的方法。发现 <= 号 打成 < 的话,运行时间天差地别。
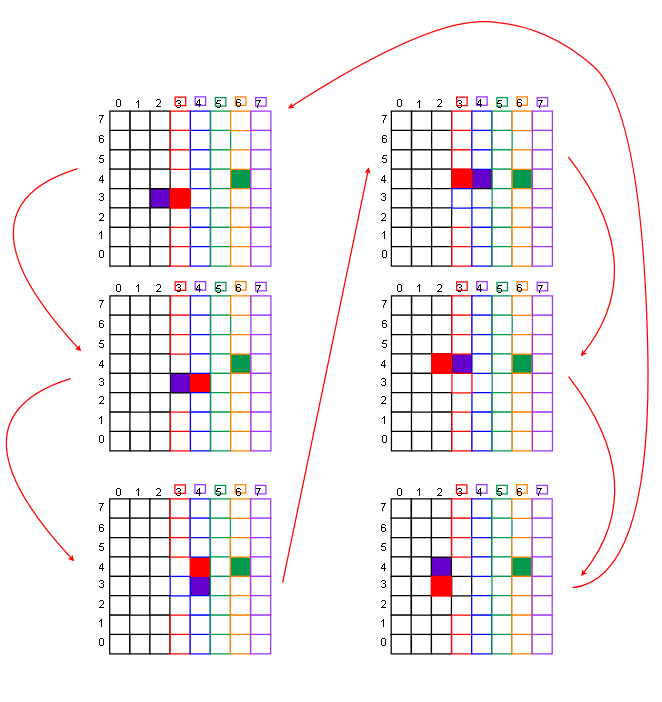
后来发现原因,没有使用数据结构来标记bfs过程中哪些点走过了,所以只能单纯用距离来判断是否访问过,如果没有不是 <= ,而是 < 的话,就会造成同样状态重复访问
如下就是一个访问循环
代价如下
表现在代码上就只是一个 <= 和 < 的区别,速率却快了 200倍不只,所以BFS和DFS一定要做好标记!
//17ms
if ((distance = distances.get(nextState)) != null && distance <= fatherDistance + 1) { continue; }
//457ms
if ((distance = distances.get(nextState)) != null && distance < fatherDistance + 1) { continue; }
可能会有疑问,为什么是用人的位置 + 箱子的位置 做为状态,而不是只用箱子的位置?不是重点研究箱子吗?
举极端例子,紫色=人,红色=箱子,绿色=Target终点,黑色=墙
如果只考虑箱子的位置,简单看出 情况2是由情况1 变化而来的,情况2比情况1移动箱子的次数多
但是情况1和情况2的箱子位置相同,所以情况2被忽略,而情况1必须变成情况2才能把箱子推到绿色的Target,情况1自己无法直接把箱子推到Target
最后的结果是无法到达Target,误判。
读者可能还有个问题:A* 寻路真的能保证箱子移动最少次数吗?A* 考虑的是 移动距离 + 曼哈顿距离 的和,找的是综合最短的路径。最短路径,必然是箱子移动距离最少。
其实A* 算法是 迪杰斯特拉 + 启发算法(曼哈顿距离)的综合体,其中迪杰斯特拉可以找到最短路径,而启发函数只是加快了 箱子向Target终点的收敛速度
还有一个疑问:怎么判断人是否可以推动箱子?
首先要保证人能到推动箱子的那个位置
下图为例:如果人(紫色)要把箱子(红色)推到位置2,那么人应该要能达到位置4才可以,也就是原本箱子位置的反方向
其实很简单,只要从人的位置开始,bfs到这个位置就可以了。bfs 的路程上遇到墙就不访问
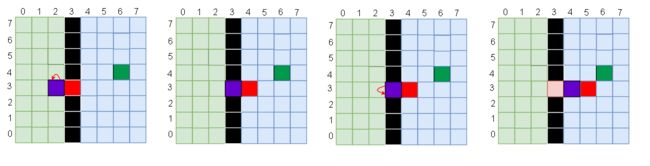
但是需要注意一种特殊情况:人是不能穿过箱子的(黑色 = 墙,红色=箱,紫色=人,绿色=Target终点)
下面这种情况,人就无法直接到达2,把箱子推到4
接着这张图讨论:
但是对人只用bfs的话,人还是会像无头苍蝇一样乱窜,窜到位置4,所以,接下去的想法和对箱子的想法类似,要减少状态,加速人到位置4的收敛速度。
但是对人不需要使用 A* ,只需要使用启发函数就足够了,因为对于人,我们只用判断是否能到达位置4。也就是之前的A*算法,把 f = g + h , 改为 f = h
不需要步数(g)影响优先级,只需要快速收敛即可。(人用heuristic + 箱子用A*)
但是,每次判断人是否能到某个指定位置(比如位置4)都要至少曼哈顿距离次访问(比如下图就是 2 + 1 次访问),才能知道是否能到达那个位置。
而且是没有障碍物的前提下,有障碍物时间复杂度会更高。
我们对于人的判断只用判断能不能到就可以了,是否有一种算法能做到直接告诉我是否能到呢(时间复杂度O(1))?而不用搜索?
这就是我们的最后一步优化:
Tarjan算法:
使用Tarjan算法的目的是找到所有的强连通分量
强连通分量在有向图中指的是可以互相访问的节点和他们的边形成的子图
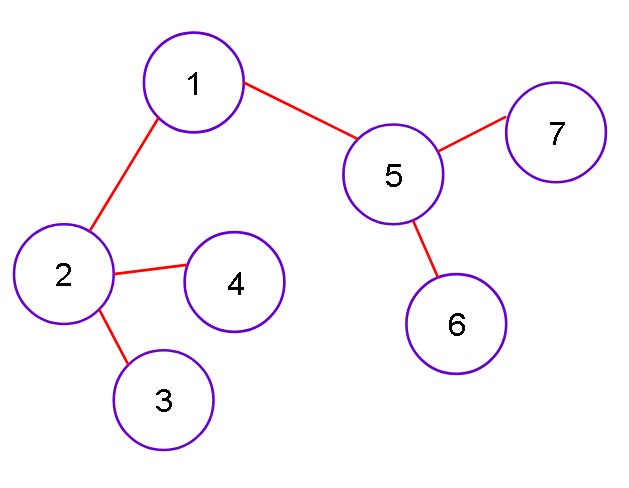
比如:下图中 2, 3, 4 以及他们互联的边组成的子图就是一个强连通分量,5,6,7亦同
在无向图中,只要两个点相邻,就可以认为两者能相互连通,所以无向图形成强连通较为简单。
下图中1,2,3,4,5,6,7 形成强连通分量
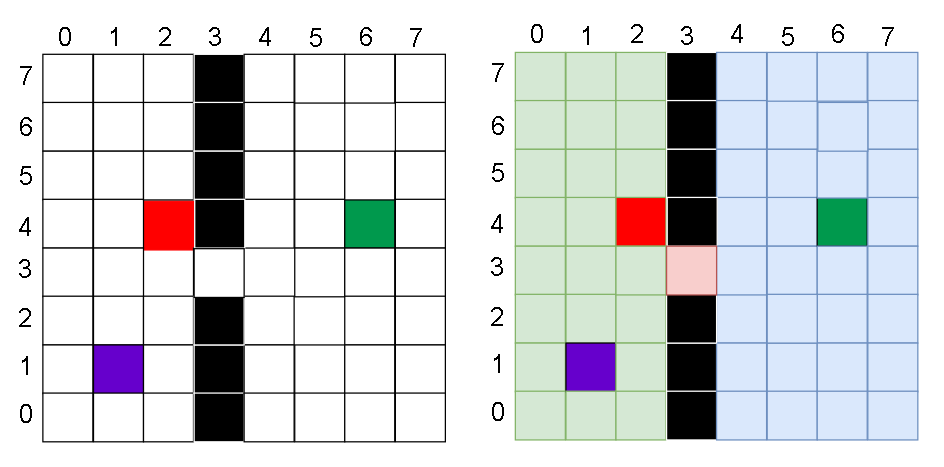
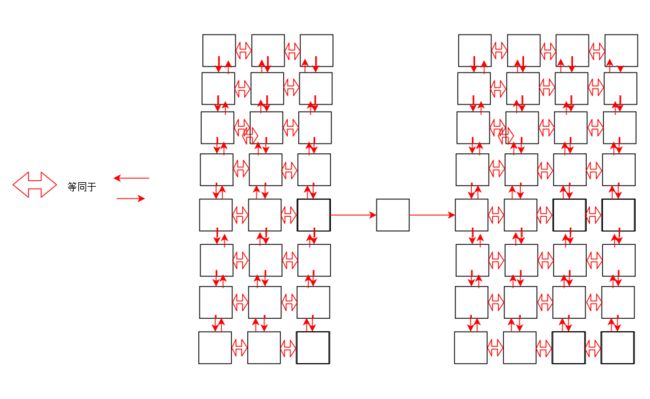
把地图的每个方格看成是图的节点,把整个地图看成有向图,下图黑色的是墙,那么整个地图被分割成左边的绿色强连通分量和右边蓝色的强连通分量。
我们想通过颜色,或者说为同一个强连通分量里的所有方格(位置)赋上一个相同的值,这样就可以直接判断玩家是否能从一个点到另一个点,如果两点的值不同,则不属于同一个强连通
分量,不能到达。判断的时间复杂度从最坏情况的 O(N) (N 为方格数,最坏情况是几乎所有点都访问才确定是否能到达) 降为 O(1);
以下的地图被分为三个强连通分量,每种颜色代表一个。
但是实际上,这个方法是有BUG的,必须箱子一开始和人在同一个强连通分量才能正确执行。
像下面这种情况,因为人无法到达箱子周围的 1, 2, 3,4 这四个中的任一位置(因为人在绿色强连通分量,4个位置都在蓝色强连通分量,颜色不同)
虽然人是能推箱子到Target的,但是会误判成无法推到Target
LeetCode 的测试用例不足?让我过了?
18个测试用例。
98%,还差2%,也许是一些细节上还有待改进
heuristic + A* :
public class HeuristicAstart { //浪费了一个下午的教训 : 不要乱用位运算,算hashCode是先移位再异或,不然会移出边界的 //还有就是,迪杰斯特拉的距离,只要是 之前的距离 <= 当前距离,都可以弃掉当前的距离不用 //哇,这个真的是,浪费了我一个下午排查 static int count = 0; static int skip = 0; static int stateCount = 0; public int minPushBox(char[][] grid) { doMain(grid); return walk(); } static Vector boxStart; static Vector myStart; static Vector target; static Astart.TarJan jan; static char[][] map; static Vector[] ops = new Vector[]{new Vector(-1, 0), new Vector(1, 0), new Vector(0, -1), new Vector(0, 1)}; final static class Vector implements Comparable { public int[] vec; double priority; int hashCode;public void setPriority(double priority) { this.priority = priority; } public Vector(int... vec) { this.vec = vec; for (int value : vec) { this.hashCode <<= 8; this.hashCode |= value; } } public Vector combine(Vector b) { int[] cA = new int[vec.length + b.vec.length]; System.arraycopy(vec, 0, cA, 0, vec.length); System.arraycopy(b.vec, 0, cA, vec.length, b.vec.length); return new Vector(cA); } public Vector slice(int from, int to) { int[] vec1 = new int[to - from + 1]; if (to + 1 - from >= 0){ System.arraycopy(vec, from, vec1, 0, to + 1 - from); } return new Vector(vec1); } public Vector add (Vector vector) { int[] vec1 = new int[vector.vec.length]; for (int i = 0; i < vec.length; i ++) { vec1[i] = vec[i] + vector.vec[i]; } return new Vector(vec1); } public Vector sub (Vector vector) { int[] vec1 = new int[vector.vec.length]; for (int i = 0; i < vec.length; i ++) { vec1[i] = vec[i] - vector.vec[i]; } return new Vector(vec1); } public double distancePow2(Vector vector) { double res = 0; for (int i = 0; i < vec.length; i ++) { res += Math.abs(vector.vec[i] - vec[i]); } return res; }
//减少 hashCode 的重复运算 @Override public int hashCode() { return hashCode; } @Override public int compareTo(Object o) { if (!(o instanceof Vector)) { throw new RuntimeException("Not a vector"); } Vector vector = (Vector) o; return (int) (this.priority - vector.priority); } @Override public boolean equals(Object o) { if (!(o instanceof Vector)) { throw new RuntimeException("Not a vector"); } Vector vector = (Vector) o; return vector.hashCode == this.hashCode; } } public static void doMain(char[][] set){ map = set; for (int i = 0 ; i < set.length; i ++) { for (int j = 0; j < set[0].length; j ++) { if (set[i][j] == 'S') { myStart = new Vector(j, i); } if (set[i][j] == 'B') { boxStart = new Vector(j, i); } if (set[i][j] == 'T') { target = new Vector(j, i); } } } } public static int playerGoTo(Vector from, Vector to, Vector nowBox) { PriorityQueuestates = new PriorityQueue (16); Set mark = new HashSet<>(16); states.add(from); while (!states.isEmpty()) { Vector now = states.poll(); if (mark.contains(now)) { continue; } mark.add(now); for (Vector op : ops) { Vector nowPos = now.add(op); if (nowPos.equals(nowBox)) { continue; } if (inRange(nowPos)) { if (nowPos.equals(to)) { return 1; } nowPos.setPriority(nowPos.distancePow2(to)); states.add(nowPos); } } } return -1; } public static boolean inRange (Vector vector) { return (vector.vec[0] >= 0 && vector.vec[0] < map[0].length && vector.vec[1] >= 0 && vector.vec[1] < map.length) && map[vector.vec[1]][vector.vec[0]] != '#'; } public static boolean inRange (int x , int y) { return (x >= 0 && x < map[0].length && y >= 0 && y < map.length) && map[y][x] != '#'; } public static boolean isTarget (Vector vector) { return vector.equals(target); } public static int walk () { PriorityQueue states = new PriorityQueue (16); Vector startState = boxStart.combine(myStart); Set mark = new HashSet<>(); startState.setPriority(boxStart.distancePow2(target)); states.add(startState); while (!states.isEmpty()) { // 状态弹出 Vector now = states.poll(); if (mark.contains(now)) { continue; } mark.add(now); Vector nowBox = now.slice(0, 1); if (isTarget(nowBox)) { return now.step; } Vector nowPlayer = now.slice(2, 3); for (Vector op : ops) { Vector nextBox = nowBox.add(op); if (!inRange(nextBox)){ continue; } Vector playerNeeding = nowBox.sub(op); if (!inRange(playerNeeding)){ continue; } Vector nextState = nextBox.combine(nowBox); if (playerGoTo(nowPlayer, playerNeeding, nowBox) == -1) { continue; } nextState.step = now.step + 1; nextState.setPriority(nextState.step + nextBox.distancePow2(target)); states.add(nextState); } } return -1; } }
Tarjan + A*:
import java.util.HashSet; import java.util.PriorityQueue; import java.util.Set; import java.util.Stack; /** * @description: * @author: HP * @date: 2020-08-09 15:58 */ public class TarjanAstart { static Vector boxStart; static Vector myStart; static Vector target; static TarJan jan; static char[][] map; static Vector[] ops = new Vector[]{new Vector(-1, 0), new Vector(1, 0), new Vector(0, -1), new Vector(0, 1)}; final static class TarJan{ int[][] tarMap; int[][] timeMap; Stackstack = new Stack<>(); int count = 0; public TarJan(char[][] map) { tarMap = new int[map.length][map[0].length]; timeMap = new int[map.length][map[0].length]; tarjan(map); } public int getPoint (int x, int y) { return (x << 16) | y; } public void tarjan(char[][] map) { tarjan(new boolean[map.length][map[0].length], map, boxStart.vec[0], boxStart.vec[1], boxStart.vec[0], boxStart.vec[1]); } private int tarjan(boolean[][] mark, char[][] map, int x, int y, int px, int py){ count ++; tarMap[y][x] = count; timeMap[y][x] = count; int min = count; mark[y][x] = true; int mine = getPoint(x, y); stack.push(mine); for (Vector p : ops) { int nextX = x + p.vec[0]; int nextY = y + p.vec[1]; if (!inRange(nextX, nextY)) { continue; } if (mark[nextY][nextX]) { //或者 if (nextY != py || nextX != px) { min = Math.min(min, tarMap[nextY][nextX]); } } else { min = Math.min(min, tarjan(mark, map, nextX, nextY, x, y)); } } //mark[y][x] = false; tarMap[y][x] = Math.min( tarMap[y][x] , min); if (tarMap[y][x] == timeMap[y][x]) { int point = stack.pop(); // 把点都取出来 while (point != mine) { int nowX = point >>> 16; int nowY = point & ((1 << 16) - 1) ; tarMap[nowY][nowX] = tarMap[y][x]; point = stack.pop(); } } return min; } public boolean connect (int x, int y, int x1, int y1) { return tarMap[y][x] == tarMap[y1][x1]; } } final static class Vector implements Comparable { public int[] vec; double priority; int hashCode; int step; public void setPriority(double priority) { this.priority = priority; } public Vector(int... vec) { this.vec = vec; for (int value : vec) { this.hashCode <<= 8; this.hashCode |= value; } } public Vector combine(Vector b) { int[] cA = new int[vec.length + b.vec.length]; System.arraycopy(vec, 0, cA, 0, vec.length); System.arraycopy(b.vec, 0, cA, vec.length, b.vec.length); return new Vector(cA); } public Vector slice(int from, int to) { int[] vec1 = new int[to - from + 1]; if (to + 1 - from >= 0){ System.arraycopy(vec, from, vec1, 0, to + 1 - from); } return new Vector(vec1); } public Vector add (Vector vector) { int[] vec1 = new int[vector.vec.length]; for (int i = 0; i < vec.length; i ++) { vec1[i] = vec[i] + vector.vec[i]; } return new Vector(vec1); } public Vector sub (Vector vector) { int[] vec1 = new int[vector.vec.length]; for (int i = 0; i < vec.length; i ++) { vec1[i] = vec[i] - vector.vec[i]; } return new Vector(vec1); } public double distancePow2(Vector vector) { double res = 0; for (int i = 0; i < vec.length; i ++) { res += Math.abs(vector.vec[i] - vec[i]); } return res; } @Override public int hashCode() { return hashCode; } @Override public int compareTo(Object o) { if (!(o instanceof Vector)) { throw new RuntimeException("Not a vector"); } Vector vector = (Vector) o; return (int) (this.priority - vector.priority); } @Override public boolean equals(Object o) { if (!(o instanceof Vector)) { throw new RuntimeException("Not a vector"); } Vector vector = (Vector) o; return vector.hashCode == this.hashCode; } } public static void doMain(char[][] set){ map = set; for (int i = 0 ; i < set.length; i ++) { for (int j = 0; j < set[0].length; j ++) { if (set[i][j] == 'S') { myStart = new Vector(j, i); } if (set[i][j] == 'B') { boxStart = new Vector(j, i); } if (set[i][j] == 'T') { target = new Vector(j, i); } } } jan = new TarJan(map); } public static int playerGoTo(Vector from, Vector to, Vector nowBox) { PriorityQueue states = new PriorityQueue (16); Set mark = new HashSet<>(16); states.add(from); while (!states.isEmpty()) { Vector now = states.poll(); if (mark.contains(now)) { continue; } mark.add(now); for (Vector op : ops) { Vector nowPos = now.add(op); if (nowPos.equals(nowBox)) { continue; } if (inRange(nowPos)) { if (nowPos.equals(to)) { return 1; } nowPos.setPriority(nowPos.distancePow2(to)); states.add(nowPos); } } } return -1; } public static boolean inRange (Vector vector) { return (vector.vec[0] >= 0 && vector.vec[0] < map[0].length && vector.vec[1] >= 0 && vector.vec[1] < map.length) && map[vector.vec[1]][vector.vec[0]] != '#'; } public static boolean inRange (int x , int y) { return (x >= 0 && x < map[0].length && y >= 0 && y < map.length) && map[y][x] != '#'; } public static boolean isTarget (Vector vector) { return vector.equals(target); } public static int walk () { PriorityQueue states = new PriorityQueue (16); Vector startState = boxStart.combine(myStart); Set mark = new HashSet<>(); startState.setPriority(boxStart.distancePow2(target)); states.add(startState); startState.step = 0; while (!states.isEmpty()) { // 状态弹出 Vector now = states.poll(); if (mark.contains(now)) { continue; } mark.add(now); Vector nowBox = now.slice(0, 1); if (isTarget(nowBox)) { return now.step; } Vector nowPlayer = now.slice(2, 3); for (Vector op : ops) { Vector nextBox = nowBox.add(op); if (!inRange(nextBox)){ continue; } Vector playerNeeding = nowBox.sub(op); if (!inRange(playerNeeding)){ continue; } Vector nextState = nextBox.combine(nowBox); if (!jan.connect(nowPlayer.vec[0], nowPlayer.vec[1], playerNeeding.vec[0], playerNeeding.vec[1])){ continue; } nextState.step = now.step + 1; nextState.setPriority(nextState.step + nextBox.distancePow2(target)); states.add(nextState); } } return -1; } }