Java知识梳理之线性表、堆栈、队列、树和堆(四)
部分源码的Github网址为:https://github.com/hzka/JavaBook02/tree/master/chap20 将Java语言程序设计基础篇刷的差不多了,开始刷Y.Daniel Liang的Java语言程序设计进阶篇,分一个第六版、第八版和第十版。本帖子是采用第六版(PS:图书馆好像只有第六版,真的是...),从下一章节开始用第十版。书的封面如下:
(一)线性表、栈与队列的基础概念(参考P2001项目)
1.1.相关定义
数据结构不仅存储数据,而且支持访问与处理;线性表是顺序存储的,支持插入删除操作;堆栈是特殊线性表,在一段执行插入删除操作,这一段称之为栈顶(后进先出);队列后端(队尾)插入,队伍前端(队首)进行删除操作(先进先出),二叉树有效进行数据查找、删除、排序和插入等操作;堆适合开发有效排序和优先队列算法。
1.2.线性表
1.2.1 线性表定义
譬如书籍列表、城市列表等等。实现线性表有两种方法:(1)动态数组存储元素,超过数组容量,创建更大数组,将当前数据组元素复制到新建数组中。MyArrayList(2)链表结构,每个结点动态生成存储元素。MyLinkedList。相同操作采用接口或者抽象类生成。
UML图如下所示:
代码如下所示:
public class Node {
Object element;
Node next;
public Node(Object o){
element = o;
}
}//使用接口来表示弱关系(类属关系),表示对象拥有某种属性,譬如:所有字符串都是可以比较的。
public interface Mylist {
public void add(Object o);
public void add(int index, Object o);
public void clear();
public Object get(int index);
public int indexOf(Object o);
public boolean contains(Object o);
public boolean isEmpty();
public int lastIndexof(Object o);
public boolean remove(Object o);
public int size();
public Object remove(int index);
public Object set(int index, Object o);
}
//描述父子关系的强关系,譬如使用GeometricObject类实现了几何对象的共有特征。
public abstract class MyAbstractList implements Mylist {
protected int size = 0;
protected MyAbstractList() {
}
protected MyAbstractList(Object[] objects) {
for (int i = 0; i < objects.length; i++) {
this.add(objects[i]);
}
}
@Override
public void add(Object o) {
add(size, o);
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public int size() {
return size;
}
@Override
public boolean remove(Object o) {
if(indexOf(o)>=0){
remove(indexOf(o));
return true;
}else{
return false;
}
}
}
1.2.2 数组线性表实现
固定大小,一旦创建,无法改变。超过容量,创建更大数组。插入新元素,先判断是否有空间,若没有,创建当前里两倍大小新数组,复制过去。移动时整体后移,删除时整体前移。使用System.arraycopy进行数组的复制。因为存储的都是对象,所以需要讲int类型数字包装成Integer类型的对象。
public class MyArrayList extends MyAbstractList {
public static final int INITAL_CAPCITY = 16;
private Object[] data = new Object[INITAL_CAPCITY];
public MyArrayList() {
}
public MyArrayList(Object[] objects) {
data = objects;
size = objects.length;
}
@Override
public void add(int index, Object o) {
//先判断是否有空间,若没有,创建当前里两倍大小新数组,复制过去
ensureCapcity();
//移动时整体后移
for (int i = size - 1; i >= index; i--) {
data[i + 1] = data[i];
}
//在指定位置放置数组,顺便增加数组长度。
data[index] = o;
size++;
}
private void ensureCapcity() {
if (size >= data.length) {
Object[] newData = new Object[data.length * 2];
System.arraycopy(data, 0, newData, 0, data.length);
data = newData;
}
}
@Override
public void clear() {
data = new Object[INITAL_CAPCITY];
}
@Override
public Object get(int index) {
return null;
}
@Override
public int indexOf(Object o) {
for (int i = 0; i < size; i++) {
if (o.equals(data[i])) return i;
}
return -1;
}
@Override
public boolean contains(Object o) {
for (int i = 0; i < size; i++) {
if (o.equals(data[i]))
return true;
}
return false;
}
//反向遍历获取最后一个该元素的位置
@Override
public int lastIndexof(Object o) {
for (int i = size - 1; i >= 0; i--) {
if (o.equals(data[i])) return i;
}
return -1;
}
@Override
public Object remove(int index) {
Object o = data[index];
for (int j = index; j < size - 1; j++) {
data[j] = data[j + 1];
}
size--;
return o;
}
@Override
public Object set(int index, Object o) {
Object old = data[index];
data[index] = o;
return old;
}
@Override
public String toString() {
StringBuffer result = new StringBuffer("[");
for (int i = 0; i < size; i++) {
result.append(data[i]);
if (i < size - 1) result.append(",");
}
return result.toString() + "]";
}
}
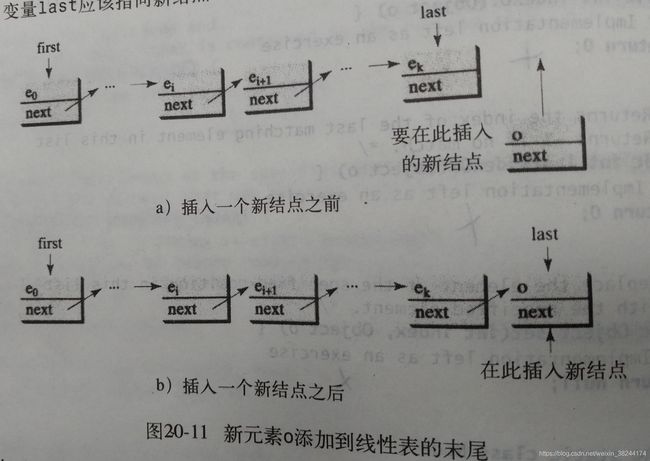
1.2.3 链表实现
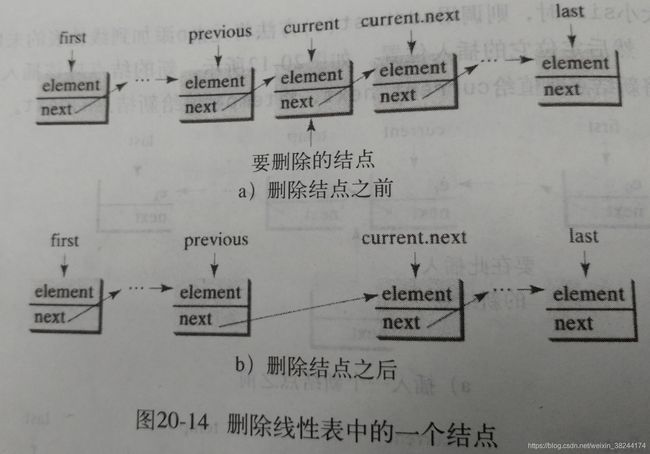
数组线性表add和set,add线性表尾增加元素是可行的。但add、remove效率低下,为提高效率,可以使用链表结构来实现线性表。新建MyLinkedList扩展自MyAbstractList。注意当设计remove时,考虑四种情况:(1)当Index超过线性表范围(index<0||index>=size),返回null;(2)当index为0时,调用removeFirst()方法删除线性表的第一个结点;(3)当index等于size-1时,调用removelast删除最后一个结点。(4)当找到index指定位置时,使用current指向该结点,previous指向该结点的上一个结点,将current.next赋值给previous.next,删除结点。(告诉我们第一多考虑各种情况,第二学会复用代码),实现了一些方法,一些方法没有实现。
//链表由结点构成,每一个节点包含一个元素,并且与下一个结点链接。
public class MyLinkedList extends MyAbstractList {
private Node first, last;
public MyLinkedList() {
}
public MyLinkedList(Object[] objects) {
super(objects);
}
public Object getFirst() {
if (size == 0) return null;
else
return first.element;
}
public Object getLast() {
if (size == 0) return null;
else
return last.element;
}
//头插法将元素插入链表
public void addFirst(Object o) {
Node newNode = new Node(o);
newNode.next = first;
first = newNode;
size++;
if (last == null)
last = first;
}
//尾插法将元素插入链表
public void addLast(Object o) {
if (last == null) {
first = last = new Node(o);
} else {
last.next = new Node(o);
last = last.next;
}
size++;
}
@Override
public void add(int index, Object o) {
if (index == 0) addFirst(o);
else if (index >= size) addLast(o);
else {
Node current = first;
//一直遍历到当下的节点。
for (int i = 1; i < index; i++) {
current = current.next;
}
//感觉写的很low。
// Node temp = current.next;
// current.next = new Node(o);
// current.next.next = temp;
Node temp = new Node(o);
temp.next = current.next;
current.next = temp;
size++;
}
}
//多考虑一些情况,长度是不是为零等等。
public Object removeFDirst() {
if (size == 0) return null;
else {
Node temp = first;
first = first.next;
size--;
if (first == null) last = null;
return temp.element;
}
}
public Object removeLast() {
return null;
}
@Override
public void clear() {
}
@Override
public Object get(int index) {
return null;
}
@Override
public int indexOf(Object o) {
return 0;
}
@Override
public boolean contains(Object o) {
return false;
}
@Override
public int lastIndexof(Object o) {
return 0;
}
@Override
public Object remove(int index) {
if ((index < 0) || (index > size)) return null;
else if (index == 0) return removeFDirst();
else if (index == size - 1) return removeLast();
else {
Node current = first;
for (int i = 1; i < index; i++) {
current = current.next;
}
Node temp = current.next;
current.next = temp.next;
size--;
return temp.element;
}
}
@Override
public Object set(int index, Object o) {
return null;
}
@Override
public String toString() {
StringBuffer result = new StringBuffer("[");
Node current = first;
for (int i = 0; i < size; i++) {
result.append(current.element);
current = current.next;
if (current != null) result.append(",");
else result.append("]");
}
return result.toString();
}
}
1.3.栈和队列(参考P2006项目)
1.3.1 定义
栈是特殊线性表,访问、插入、删除只能在栈顶进行;队列也是特殊线性表,在一端(队尾)插入,在开始端(队列头)访问和删除。两种方法:(1)使用继承:扩展数组线性表的类来声明栈类,扩展链表类来声明队列类;(2)使用包容:将数组线性表声明为栈类中的数据域,将链表声明为队列类中的数据域。包容更好一些,声明全新栈类和队列类。
1.3.2 代码示例
对一个栈来说,push(o)是将一个元素添加到栈顶;pop方法是将栈顶的元素删除并返回该元素。对一个队列而言,enqueue(o)是将一个元素添加在队尾,dequeue方法是将队列头的元素删除。
public class MyStack {
private MyArrayList list =new MyArrayList();
public void push(Object o){
list.add(o);
}
public Object pop(){
Object o = list.remove(list.size-1);
return o;
}
@Override
public String toString() {
return "Stack:"+list.toString();
}
}
public class MyQueue {
private MyLinkedList list = new MyLinkedList();
//队尾插入
public void enqueque(Object o) {
list.addLast(o);
}
//队头删除
public Object dequeue() {
return list.removeFDirst();
}
public int getSize() {
return list.size;
}
@Override
public String toString() {
return "Queue" + list.toString();
}
}
(二).二叉树(参考P2008项目)
2.1 定义
二叉树是一种层次结构,二叉树的每一个结点都有0个、1个或者2个分支。左孩子、右孩子、叶子结点的定义不再赘述。二叉查找树的特征:每一个结点左子树结点的值小于该结点的值,右子树结点的值都大于该结点的值。
2.2 二叉树的表示
public class TreeNode {
Object element;
TreeNode left;
TreeNode right;
public TreeNode(Object o){
element = o;
}
}
2.3 二叉查找树中插入元素
若二叉树为空,则使用新元素创建一个根结点,否则为新元素查找父结点,若新元素的值小于父结点的值,则将新元素的结点设置为父结点的左孩子;否则,将其设为右孩子。
2.4 二叉树的遍历
树的遍历就是访问树中每个结点的过程,要求每个结点只访问一次。分为前序、中序、后序、深度优先和广度优先等遍历方法。
中序遍历:左根右,对于二叉查找树而言,是递增顺序的。
前序遍历:根左右
后序遍历:左右根
广度优先:第一次访问根节点,从左往右一次访问根节点的所有孩子,再一层层访问。
2.5代码实现
Insert方法是为元素object创建一个节点,并将它插入树中,若为空树,则该结点称为根节点,否则,该方法为它寻找一个能够保持搜索树顺序的父节点,如果在树中找到该元素,返回true,否则返回false。Inorder是中序遍历,先递归遍历左子树,再遍历根,最后遍历右子树,当树为空时,遍历结束。其余类似。
public class BinaryTree {
private TreeNode root;
private int size = 0;
public BinaryTree() {
}
public BinaryTree(Object[] objects) {
for (int i = 0; i < objects.length; i++) {
insert(objects[i]);
}
}
//将节点插入进树中。
public boolean insert(Object object) {
if (root == null) root = new TreeNode(object);//将object类型包装一下。
else{
//定位父亲节点
TreeNode parent = null;
TreeNode current = root;
//1.查找新元素的父节点。
while (current!=null){
if(((Comparable)object).compareTo(current.element)<0){
parent = current;
current = current.left;
}else if(((Comparable)object).compareTo(current.element)>0){
parent = current;
current = current.right;
}else{
return false;//重复节点不添加。
}
}
//2.找到父亲节点后,进行插入操作。这块相当于是拿引用,直接给引用赋值,这样root底下的所有节点也会和parent一样
// 得到更新。
if(((Comparable)object).compareTo(parent.element)<0){
parent.left = new TreeNode(object);
}else{
parent.right = new TreeNode(object);
}
}
size++;
return true;
}
//中序遍历
public void inorder(){
inorder(root);
}
//左根右,递归法
public void inorder(TreeNode root){
if(root == null) return;
inorder(root.left);
System.out.println(root.element+" ");
inorder(root.right);
}
public void postorder(){
postorder(root);
}
public void postorder(TreeNode root){
if(root == null) return;
postorder(root.left);
postorder(root.right);
System.out.println(root.element+" ");
}
public void preorder(){
preorder(root);
}
public void preorder(TreeNode root){
if(root == null) return;
System.out.println(root.element+" ");
preorder(root.left);
preorder(root.right);
}
public int getSize() {
return size;
}
}
public class Main {
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.insert("George");
tree.insert("Michael");
tree.insert("Tom");
tree.insert("Adam");
tree.insert("Jones");
tree.insert("Peter");
tree.insert("Daniel");
System.out.println("Inorder:");
tree.inorder();
System.out.println("\nPostorder:");
tree.postorder();
System.out.println("\nPreorder:");
tree.preorder();
System.out.println("\nSize is"+tree.getSize());
}
}(三).堆(堆和队列参考P2010项目)
3.1定义
堆是具有以下特征的二叉树:(1)它是一个完全二叉树;(2)每个结点都大于等于它的任何孩子节点。所谓完全二叉树,指的是除了最后一层之外的每一层都是满的,而且最后一层的叶子都在最左边。
3.2堆的表示
可以使用二叉树表示堆,但如果预先不知道堆的大小,那么使用数组或数组线性表也是一个不错的选择。此时,对位置i处的结点,它的左孩子位于位置2i+1处,它的右孩子在2i+2处,它的父亲在(i-1/2)处。譬如下图:39结点在位置4处,它的左孩子在9,它的右孩子在10处,它的父亲在1处。
3.3删除根结点
注意删除后,必须保持堆得特征。譬如下图的删除结点62以后的重建堆过程。(1)先将最右下角(最后)一个节点(9)放在根处,(2)然后交换9和59,与第二层中的最大值进行交换。(3)依次类推,重建了堆。
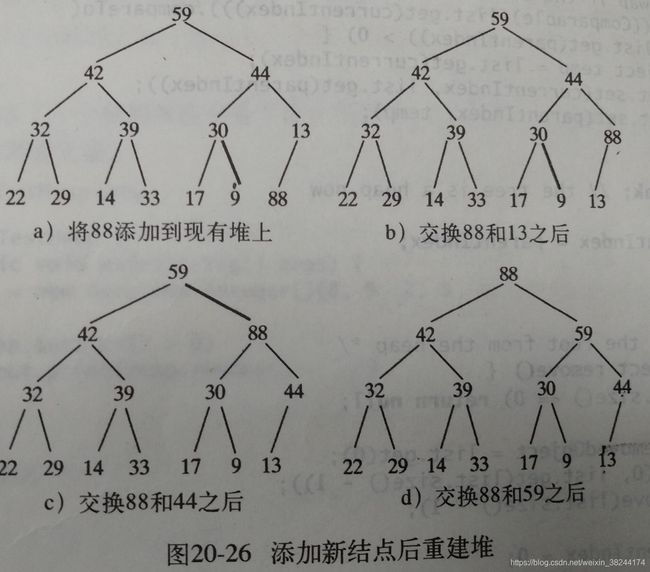
3.4添加新节点
(1)在堆尾添加一个新结点(2)与该新节点的父亲节点进行比较,若大于,交换,否则,处于原位置。(3)依次类推,直到根部。
3.5代码实现
add方法将对象追加到树中,大于父节点,进行交换,一直持续到新对象称为根节点,或者不大于其父节点为止。Remove删除根节点,保持对的特征,将最后一个对象移到根处。
public class Heap {
private ArrayList list = new ArrayList();
public Heap() {
}
public Heap(Object[] objects) {
for (int i = 0; i < objects.length; i++) {
add(objects[i]);
}
}
public void add(Object newobject) {
//1.先在队尾添加新结点。
list.add(newobject);
//2.确定当前的下标。更新结点的值。原理很简单,只是Arraylist的简单拓展。
int currentIndex = list.size() - 1;
while (currentIndex > 0) {
int parentIndex = (currentIndex - 1) / 2;
if (((Comparable) (list.get(currentIndex))).compareTo(list.get(parentIndex)) > 0) {
Object temp = list.get(currentIndex);
list.set(currentIndex, list.get(parentIndex));
list.set(parentIndex, temp);
} else break;
currentIndex = parentIndex;
}
}
public Object remove() {
if (list.size() == 0) return null;
//1.获取第零个元素,将最后一个元素放在第零个元素处。然后移除掉最后一个元素。
Object removeObject = list.get(0);
list.set(0, list.get(list.size() - 1));
list.remove(list.size() - 1);
int currentIndex = 0;
while (currentIndex < list.size() - 1) {
int leftchildIndex = currentIndex * 2 + 1;
int rightchildIndex = currentIndex * 2 + 2;
//2.判断准备替换哪一个结点,替换左孩子结点还是右孩子节点。
if (leftchildIndex >= list.size()) break;
int maxIndex = leftchildIndex;
if (rightchildIndex < list.size()) {
if (((Comparable) (list.get(maxIndex))).compareTo(list.get(rightchildIndex)) < 0) {
maxIndex = rightchildIndex;
}
}
//3.和左右节点的最大值进行交换。
if (((Comparable) (list.get(currentIndex))).compareTo(list.get(maxIndex)) < 0) {
Object temp = list.get(maxIndex);
list.set(maxIndex,list.get(currentIndex));
list.set(currentIndex,temp);
currentIndex = maxIndex;
}else{break;}
}
return removeObject;
}
public int getSize(){
return list.size();
}
}(四).优先队列
4.1 特点
队列先进先出,队尾追加,队头移出。但在优先队列中,元素被赋予了优先级。优先队列具有最高优先级进先出的特性。譬如:医院急救室为病人赋予优先级,优先级高的病人最先治疗。考虑用堆来实现。
4.2 代码实现
public class MyPriorityQueue {
private Heap heap = new Heap();
public void enqueue(Object newObject){
heap.add(newObject);
}
public Object dequeue(){
return heap.remove();
}
public int getSize(){
return heap.getSize();
}
}public class Main {
public static void main(String[] args) {
Heap heap = new Heap(new Integer[]{8, 9, 2, 3, 4, 1, 5, 6, 7});
while (heap.getSize() > 0) {
System.out.println(heap.remove() + " ");
}
Patient patient01 = new Patient("John", 2);
Patient patient02 = new Patient("Jim", 1);
Patient patient03 = new Patient("Tim", 5);
Patient patient04 = new Patient("Cindy", 7);
MyPriorityQueue priorityQueue = new MyPriorityQueue();
priorityQueue.enqueue(patient01);
priorityQueue.enqueue(patient02);
priorityQueue.enqueue(patient03);
priorityQueue.enqueue(patient04);
while (priorityQueue.getSize()>0){
System.out.print(priorityQueue.dequeue()+" ");
}
}
static class Patient implements Comparable {
private String name;
private int priority;
public Patient(String name, int priority) {
this.name = name;
this.priority = priority;
}
@Override
public String toString() {
return name + "(Priority" + priority + ")";
}
@Override
public int compareTo(Object o) {
return this.priority - ((Patient) o).priority;
}
}
}
(五).本章小结