机器学习实战之Kaggle泰坦尼克初尝试

项目简介

项目说明：泰坦尼克号的沉没是历史上最臭名昭著的海难之一，1912年4月15日，在她的处女航中，被广泛认为的“沉没” RMS泰坦尼克号与冰山相撞后沉没。不幸的是，船上没有足够的救生艇供所有人使用，导致2224名乘客和机组人员中的1502人死亡。虽然幸存有一些运气，但似乎有些人比其他人更有可能生存。本次主要是根据提供的数据来判断什么样的人更容易生存。

数据来源：Kaggle泰坦尼克生存预测

数据说明：

PassengerId	乘客编号
Survived	是否生还（0、1）
Pclass	船票等级（1、2、3）
Name	姓名
Sex	性别（male、female）
Age	年龄
SibSp	船上的兄弟姐妹、配偶数量
Parch	船上的父母、子女数量
Ticket	票号
Fare	票价
Cabin	船舱口
mbarked	登船港口

数据分析

这部分主要进行数据的导入、查看、缺失值的处理及数据的可视化显示，目前先是针对训练数据进行分析，后续需要对训练数据和测试数据进行统计处理，保证一致性。

导入数据

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
# 导入数据
train_data = pd.read_csv("titanic_train.csv")
test_data = pd.read_csv("titanic_test.csv")

查看数据

查看前五行

# 查看数据
train_data.head()

结果如下： 

 查看整体统计

# 整体统计
train_data.describe()

结果如下：

可以看出，训练集中有891条数据，整体的生存率为38.4%，平均年龄为29.699，平均票价为32.2

查看数据缺失值

# 查看数据
train_data.info()
# 缺失值数量查看
train_data.isnull().sum()

结果如下： 

可以看到，船舱口数据缺失较大、登船港口有两条缺失、乘员年龄数据也有缺失，后续需要对缺失值进行填充。

缺失值处理

由上面可以数据有缺失，需要对其进行处理，主要是依据填充的形式，对于Embarked使用众数进行填充，对于年龄使用平均值进行填充（当然也可以根据其他特征使用模型拟合进行填充，本次为了简便使用了年龄均值的方式），对于Carbin，博主使用的是去除该特征，代码如下：

# 数据缺失值处理
# 年龄使用了平均值来填充
train_data["Age"] = train_data["Age"].fillna(train_data["Age"].mean())
# Embarked使用众数填充
train_data["Embarked"] = train_data["Embarked"].fillna(train_data["Embarked"].mode().iloc[0])
#缺失值较大的Cabin可以暂时不考虑此特征

数据可视化

本部分主要是通过数据可视化可以直观看到数据之间的关系

查看生存率

# 中文显示
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
# 生存率饼图
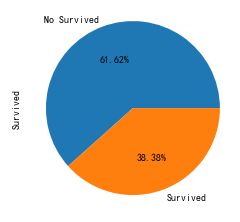
train_data["Survived"].value_counts().plot(kind='pie',autopct = '%1.2f%%',labels=['No Survived', 'Survived'])
plt.show()

结果如下： 

性别与生存率关系

# 性别与存活率的关系
train_data.groupby(["Sex","Survived"])["Survived"].count()
# 绘制柱状图
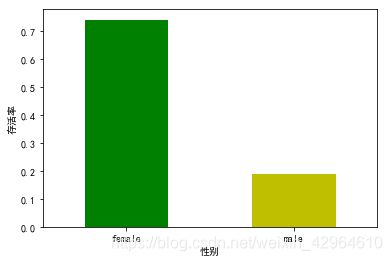
train_data.groupby("Sex")["Survived"].mean().plot(kind="bar",color=['g','y'])
plt.xlabel("性别")
plt.ylabel("存活率")
plt.xticks(rotation=0)
plt.show()

结果如下：

可以看出，女性相对男性生存率较高，体现了女士优先

船舱等级与生存率关系

# 存活率与船舱等级关系
train_data.groupby(["Pclass","Survived"])["Survived"].count()
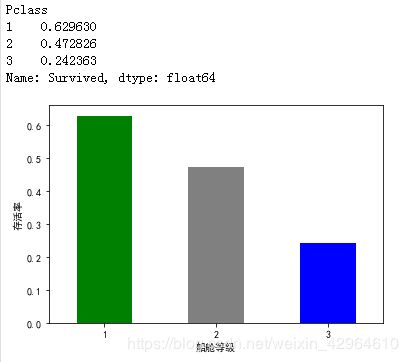
print(train_data.groupby("Pclass")["Survived"].mean())
train_data.groupby("Pclass")["Survived"].mean().plot(kind="bar",color=['g','grey','b'])
plt.xlabel("船舱等级")
plt.ylabel("存活率")
plt.xticks(rotation=0)
plt.show()

结果如下：

可以看出，生存率与船舱等级有关，等级高的生存率高，有钱真好！

同时我们也针对不同船舱查看了男、女的生存情况，如下：

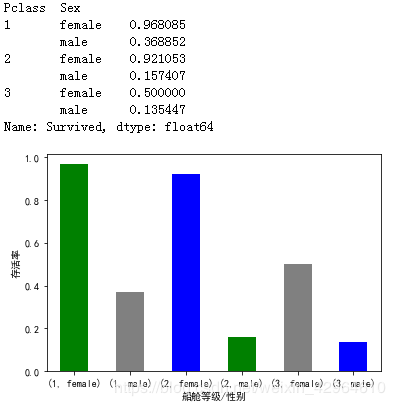
print(train_data.groupby(["Pclass","Sex"])["Survived"].mean())
train_data.groupby(["Pclass","Sex"])["Survived"].mean().plot(kind="bar",color=['g','grey','b'])
plt.xlabel("船舱等级/性别")
plt.ylabel("存活率")
plt.xticks(rotation=0)
plt.show()

结果如下：

我们可以看到，不同等级的船舱中女性存活率还是相对较高，接下来我们看看年龄和存活率的关系，如下：

# 年龄与存活率的关系
plt.figure(figsize=(18,5))
plt.subplot(1,2,1)
plt.yticks(range(0,110,10))
sns.violinplot("Pclass","Age",hue="Survived",data=train_data,split=True)
plt.title("Pclass and Age vs Survived")
plt.grid(linewidth=0.4)
plt.subplot(1,2,2)
plt.yticks(range(0,110,10))
sns.violinplot("Sex","Age",hue="Survived",data=train_data,split=True)
plt.title("Sex and Age vs Survived")
plt.grid(linewidth=0.4)
plt.show()

结果如下：

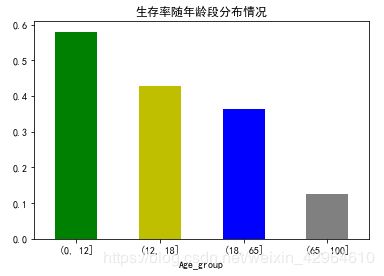
我们来看看年龄段分布和生存率的关系，如下：

# 划分年龄段
bins = [0, 12, 18, 65, 100]
train_data["Age_group"] = pd.cut(train_data["Age"], bins)
train_data["Age_group"].value_counts()
# 数据可视化
train_data.groupby("Age_group")["Survived"].mean().plot(kind="bar",color=['g','y','b','grey'])
plt.xticks(rotation=0)
plt.title("生存率随年龄段分布情况")
plt.show()

结果如下：

可以看出，年龄小的生存率较高，随着年龄的增加，生存率不断减小，体验了女儿和孩子先行。

其实还有其他相关数据的可视化，如家庭成员和生存率的关系、票价和生存率的关系、登船港口和生存率的关系、姓名相关因素和生存率的关系等，这些都与上面的实现形式类似，此处暂不一一说明了，有兴趣的可以自己实现下。

特征工程

之前我们对训练数据进行了处理分析，实际应用中，需要对训练数据和测试数据同时进行处理，从而确保数据特征的一致性，融合代码如下：

# 特征工程（对训练集和测试集同时进行处理）
test_data["Survived"] = 0
combain_data = train_data.append(test_data)

其中combain_data为融合在一起的数据，接下来对数据一起进行处理

性别转换

特征中性别的取值为male、female值，将其转换成0、1值，如下：

# 将male和female转换成数值型，male为0，female为1
train_data["Sex"] = train_data["Sex"].apply(lambda x:0 if x=="male" else 1)

港口转换

数据中港口为C、S、Q，需要将其转换成数值型，如下：

# Embarked使用众数填充
combain_data["Embarked"] = combain_data["Embarked"].fillna(combain_data["Embarked"].mode().iloc[0])
# 将Embarked（港口）转出数值型，其中S为0、C为1、Q为2
combain_data["Embarked"] = combain_data["Embarked"].apply(lambda x: 0 if x== 'S' else 1 if x == 'C' else 2)

年龄填充

本次使用年龄的平均值进行填充，当然你也可以根据其他特征通过模型模拟进行年龄填充，博主为了方便在此处使用了平均值进行填充，如下：

combain_data['Age']=combain_data['Age'].fillna( combain_data['Age'].mean())

票价填充

数据中票价存在缺失值，本次仍然使用平均值进行填充，如下：

# 对Fare进行填充(本次使用缺失值的所属港口的票价平均值进行填充，当然也可以加入年龄、是否为团体票等因素进行填充)
combain_data["Fare"] = combain_data["Fare"].fillna(combain_data.groupby("Embarked").mean()["Fare"].iloc[0])

家庭人数

将家庭总人数作为一个特征，处理如下：

# 家庭人数
combain_data["FamilySize"] = combain_data["SibSp"] + combain_data["Parch"] + 1

家庭类型

主要是根据家庭人数来判断家庭类型，此处参考了Python数据挖掘进阶--泰坦尼克号案例分析

如下：

'''
家庭类别：
小家庭Family_Single：家庭人数=1
中等家庭Family_Small: 2<=家庭人数<=4
大家庭Family_Large: 家庭人数>=5
'''
combain_data["Family_Single"] = combain_data["FamilySize"].apply(lambda x: 1 if x==1 else 0)
combain_data["Family_Small"] = combain_data["FamilySize"].apply(lambda x: 1 if 2 <= x <= 4 else 0)
combain_data["Family_Large"] = combain_data["FamilySize"].apply(lambda x: 1 if x >= 5 else 0)

当然还可以根据姓名提取其头衔、如：已婚女士、男士、未婚女士、政府官员、王室等特征、博主没有进行此方面的数据特征挖掘，本次主要是为了了解大致的处理流程，后续可以进行更深入的挖掘。

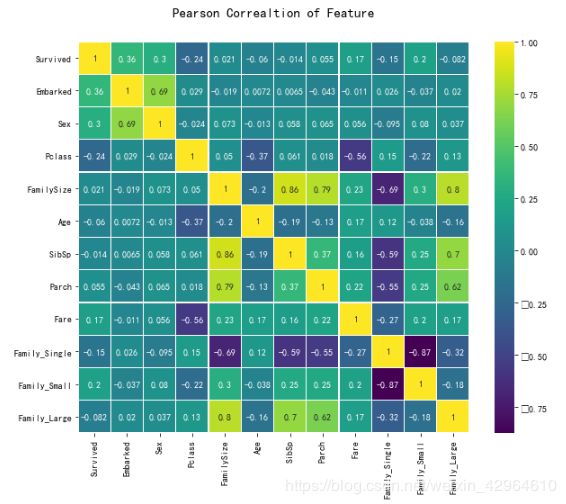
相关性计算

计算特征之间的相关性，如下：

# 计算相关性
corrDf = combain_data.corr()
corrDf['Survived'].sort_values(ascending =False)

结果如下：

绘制相关性图形，如下：

corr_data = pd.DataFrame(combain_data[['Survived','Embarked','Sex','Pclass','FamilySize','Age','SibSp','Parch','Fare','Family_Single','Family_Small','Family_Large']])
colormap = plt.cm.viridis
plt.figure(figsize=(14,12))
plt.title('Pearson Correaltion of Feature',y=1.05,size=15)
sns.heatmap(corr_data.corr(),linewidths=0.1,vmax=1.0,square=True,cmap=colormap,linecolor='white',annot=True)
plt.show()

结果如下：

特征选择

根据上面的相关性计算结果，本次选择的特征有：PassengerId、Survived、Embarked、Sex、Family_Small、Fare、Parch、FamilySize

# 特征选择（选择相关度比较大的下面几个特征）
need_data = pd.DataFrame(combain_data[['PassengerId', 'Survived','Embarked','Sex','Family_Small','Fare','Parch','FamilySize']])

 构建模型

主要是使用训练数据和选择的算法模型来得到机器学习模型，用测试数据进行模型的评估验证

划分数据集

主要对need_data数据进行训练数据集和测试数据集的划分，其中前891条为训练数据，剩余的为测试数据，具体实现如下：

# 划分数据集
# 训练数据如下:
train_data_x = need_data.iloc[0:891,2:]
train_data_y = need_data.iloc[0:891,1]
# 测试数据如下：
test_data_x = need_data.iloc[891:,2:]
test_data = need_data.iloc[891:,0:]

使用交叉验证的方式，需要对训练集再次划分，如下:

# 交叉验证数据
from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y = train_test_split(train_data_x, train_data_y, train_size=0.8, random_state=0)

模型选择

此问题为分类问题，同时为二分类问题，因为我们选择比较简单的逻辑回归算法，如下：

# 导入模型(使用逻辑回归模型)
from sklearn.linear_model import LogisticRegression
# 创建模型
model = LogisticRegression()

注：可以使用其他分类算法，另外可以加入模型融合，本文仅使用简单的逻辑回归算法。

模型训练

# 训练模型
model.fit(train_x,train_y)

结果如下：

模型评估

使用score方法进行模型评估，如下：

model.score(test_x, test_y)

结果如下：

可以看到正确率为73.18%

模型应用

模型预测，主要使用predict方法对测试集进行预测，如下：

prediction = model.predict(test_data_x)

最后我们将加过导出为CSV格式文件，便于提交到kaggle中，如下：

# 选取乘员ID及预测结果
result = pd.DataFrame({'PassengerId':test_data['PassengerId'], 'Survived':prediction.astype(np.int32)})
# 导出为csv文件
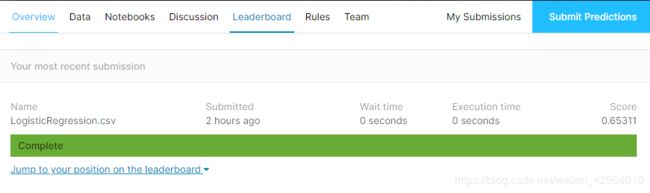
result.to_csv("LogisticRegression.csv",index=False)

提交结果

将我们生产的CSV文件提交到kaggle平台上，从而计算我们的正确率及排名，如下：

提交成功之后就可以看到我们的结果，如下，可以看出，正确率还属于比较低，排名也比较靠后，靠前的都是100%正确率，因此后续我们还需要从模型特征、算法选择，模型融合方面下手，继续优化。 

 

总结 

本次是针对比较经典的Kaggle项目，主要是为了了解机器学习的大致流程，后续需要不断完善提高自己处理相关部分内容的技能，如果你感觉对你有帮助的话不如顺手点个赞吧！