Python数独算法

最近突然对数独感兴趣，玩了好几天。慢慢摸索出了一些解题规律，就想着能不能用代码自动化实现。趁五一放假试着写了点代码，效果还行，至少不比网上一些教程里慢太多，因此就放到这里跟大家分享一下。

由于本人也是Python新手，很多语句可能不够简洁，还望见谅。

完整代码可见github链接：https://github.com/linking9230/sudoku.git

一、数独输入

我准备了两套数独题目作为测试，一套为困难难度的，另一套为专家难度。

困难：

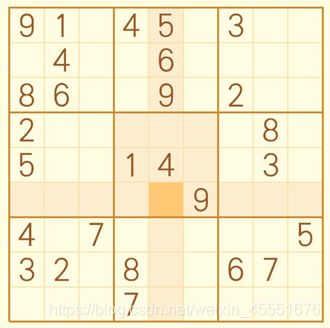
专家：

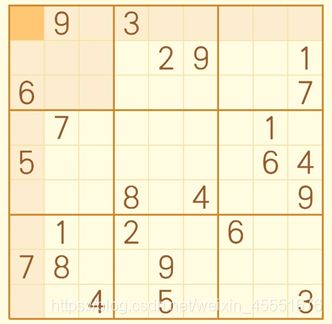
我将数据放入到CSV文件中，空白格用0代替，方便读取和识别。

二、代码实现

数独的玩法大家应该都清楚，就是每一格的取值为1-9中的一个，并且在所在行，所在列，以及所在九宫格内不能重复。而游戏的难点就在于，每一个单元格，可填入的数字会有很多，这就使得我们不得不去寻找正确的数字。

当我实际在玩时，有很多小技巧，可以相对快速的找到正确的数字。但是对于编程而言，代码的优势在于计算速度快，因此使用穷举思想，也能够较快速找到正确的数字。

因此，我的第一个想法，就是利用递归循环解决问题。

——————————————————————————————————————
首先，我需要获取任意一个单元格可填入的值列表，代码如下：

def para(i):
    r=i//9
    c=i%9
    rr=r//3
    cr=c//3
    rr_d=rr*3
    rr_u=rr*3+3
    cr_d=cr*3
    cr_u=cr*3+3
    return r,c,rr_d,rr_u,cr_d,cr_u
 
def ql(m,i):
    f_l=[0,1,2,3,4,5,6,7,8,9]
    r,c,rr_d,rr_u,cr_d,cr_u=para(i)
    a=list(set(list(m[r])+list(m[:,c])+list(m[rr_d:rr_u,cr_d:cr_u].flatten())))
    q_l=[x for x in f_l if x not in a]
    return q_l,r,c

第一个函数的目的是，我在实际循环过程中，是将99的数独矩阵，展开成了811的一维列表，方便我进行循环。而利用para函数，则可以从一维列表的index返回到9*9矩阵的参数，并且获得该单元格所在九宫格的范围（rr_d,rr_u,cr_d,cr_u即为该九宫格的行列上下限）

第二个函数也很好理解，我把所在行，所在列，所在九宫格的所有值集合起来，用一个set去重，那么剩下未出现的数字，就是该单元格可以选择的值，返回为一个列表。

——————————————————————————————————————
接着，就可以递归循环解答了（后来我才知道，这种递归循环，其实也就是深度优先循环，或者DFS算法，也算歪打正着）。

def dg(m,n,i,l,flag):
	#m:matrix
	#n:flatten matrix
	#i: 第i个单元格
	#l:最后一个空单元格的位置
	
    if flag==0:
        for j in range(i,l+1):
            if n[j]==0:
                break
        q_l,r,c=ql(m,j)
        
        if len(q_l)==0:

            flag=-1
            return flag
        if j==l and len(q_l)>1:
            flag=-1
            return flag
        for t in q_l:
            m[r,c]=t
            k=j+1
            if k==l+1:
                flag=1
                return flag
            else:
                flag=0
                flag=dg(m,n,k,l,flag)
                if flag==1:
                    break
        if flag==-1:
            m[r,c]=0
            return flag
        if flag==1:
            return flag

这一步的算法是这样的，从第一个待填单元格开始，先获取可填值列表。在该列表中循环，先选取第一个数字填入到矩阵中，在此基础上，找到下一个待填单元格，同样获取列表，再选取第一个值填入。

当然这样填下去，大概率是会出错的。一旦出错，会出现的情况就是，在某个空单元格中，可填值列表为无。当遇到这种情况时，我们就停止递归，返回到上一级，在前一个空单元格的可填列表中，选择填入下一个数字，再继续进行递归循环。假如前一个空单元格的可填列表都试过了，在下一级依然出错，那就再返回到上上一级中，选择列表的下一个可选值，如此反复。

这样之后，一定能在最后选择到合适正确的值，使得递归能够顺利进行下去，直至最后一个待填单元格。理论上来说，到了最后一个单元格时，它的可填列表一定只能剩下一个数字，因此我们这里就可以判定，一旦它的可填列表大于了1，就说明之前填入的数字有误，需要返回到上一级。

在这一过程中，我用了一个flag参数，来调控程序是返回上一级还是继续下一级循环。flag=-1表示此时出错了，不在继续循环，返回到上一级中。当flag=0时，继续递归循环。当flag=1时，说明所有数据都被正确填入了，任务完成，也就不需要继续递归了。

在函数中，我return flag是为了将下一级的判定传回上一级。这一点也是debug试错试出来的，如果不return, 上一级的flag不会发生改变，永远是0。

另外还有一点很重要的是，当第k个单元格可填值列表循环完成之后，flag仍然为-1，需要再返回到第k-1个单元格时，一定要把k单元格的数字变为0，否则会保留列表中的最后一个数字，造成错误。

最后将上述整合成一个solver函数即可

def solver1(m,n):
    
    #find the last empty cell
    
    for i in reversed(range(1,81)):
        if n[i]==0:
            l=i
            break
    flag=0
    i=0
    flag=dg(m,n,i,l,flag)
    return m

困难版运算时间为0.045秒，专家版运算时间为5.106秒。

——————————————————————————————————

完成这一步后，我就开始思考如何进一步提高算法速度。当然了，那些高级的编程技巧我是不懂的，我所能改善的，只能是引入一些人为的先验技巧。

• 寻找可填入列表只有一项的空格
  这个操作往往是我在实际玩数独中的第一步，有些空格由于受周围有数字的单元格的影响，仅能填入一个数字，那这个数字一定就是解。代码如下：

def wy(m,n): 
    flag=0
    for i in range(81):
        if n[i]==0:
            q_l,r,c=ql(m,i)
            if len(q_l)==1:
                m[r,c]=q_l[0]
                n[i]=q_l[0]
                flag=1
    return m,n,flag

由于填入一个数字后，可能会产生下一个具有唯一值的空格，因此我在主函数中用了循环，并用flag调控。当再也找不到新的唯一值空格时，就开始上述的深度遍历循环。

主函数代码如下：

def solver2(m,n):
    
    flag=1
    while flag==1:
        m,n,flag=wy(m,n)
    
    
    l=0
    for i in reversed(range(1,81)):
        if n[i]==0:
            l=i
            break
    
    if l!=0:
        flag=0
        i=0
        flag=dg(m,n,i,l,flag)
        
    return m

运行后，困难版的运算时间为0.021秒，而专家版的运算时间为5.15秒。

————————————————————————————————————

• 寻找可填列表的唯一项
  这个技巧稍微高级一点，但也不难理解。在一行中，假设有多个空格，每个空格的可填值都是一个列表，例如为[1,3,5],[1,3,6,9],[3,6,9]。在这种情况下我们可以看到，数字1,3,6,9都有可能在多个空格中出现，但是数字5，仅有可能在第一个空格中出现。因此我们就能判定，第一个空格中应该填入数字5。
  同样的判定，也能适用在一列中，或者一个九宫格中。因此就有了如下的算法：

def dq_l(m,n):
    dql={}
    for i in range(81):
        if n[i]==0:
            q_l,r,c=ql(m,i)
            dql[i]=q_l
    return dql

#check all available list in one row and find the value which only exist in one cell

def h_c(m,n):
    flag=0
    dql=dq_l(m,n)
    for i in range(9):
        la=[]
        k_l=[x for x in range(9*i,9*i+9) if x in dql.keys()]
        for k in k_l:
            la+=dql[k]
        ct=Counter(la)
        lb=[]
        
        for j,v in ct.items():
            if v==1:
                lb.append(j)
        for t in lb:
            for k in k_l:
                if t in dql[k]:
                    r,c,_,_,_,_=para(k)
                    n[k]=t
                    m[r,c]=t
                    k_l.remove(k)
                    flag=1
                    break
    dql={}
    return m,n,flag


#check all available list in one column and find the value which only exist in one cell

def v_c(m,n):
    flag=0
    dql=dq_l(m,n)
    for i in range(9):
        la=[]
        k_l=[x for x in range(i,73+i,9) if x in dql.keys()]
        for k in k_l:
            la+=dql[k]
        ct=Counter(la)
        lb=[]
        for j,v in ct.items():
            if v==1:
                lb.append(j)
        for t in lb:
            for k in k_l:
                if t in dql[k]:
                    
                    r,c,_,_,_,_=para(k)
                    n[k]=t
                    m[r,c]=t
                    k_l.remove(k)
                    flag=1
                    break            
    dql={}
    return m,n,flag

#check all available list in one square and find the value which only exist in one cell

def n_c(m,n):
    flag=0
    dql=dq_l(m,n)
    c_l=[x for x in range(0,9,3)]+[x for x in range(27,36,3)]+[x for x in range(54,63,3)]
    for i in range(9):
        la=[]
        u=c_l[i]
        n_l=[x for x in range(u,u+3)]+[x for x in range(u+9,u+12)]+[x for x in range(u+18,u+21)]
        k_l=[x for x in n_l if x in dql.keys()]
        for k in k_l:
            la+=dql[k]
        ct=Counter(la)
        lb=[]
        for j,v in ct.items():
            if v==1:
                lb.append(j)
        for t in lb:
            for k in k_l:
                if t in dql[k]:
                    r,c,_,_,_,_=para(k)
                    n[k]=t
                    m[r,c]=t
                    k_l.remove(k)
                    flag=1
                    break     
    dql={}
    return m,n,flag

在上述代码中，我先是建立了一个dql函数，目的是将所有空格的可填值做成一个字典，字典的键是空格的次序，值是列表。

接着，在h_c函数中，我逐行进行检查。先获取行中所有空格的位置，在dql字典中，将所有空格的列表集合起来，并使用Counter函数进行统计，找到仅出现1次的数字。一行中有可能会出现不止一个出现次数为1的数字，因此获得的是一个列表。那么在列表中循环，反向去找到该数字对应的空格，将该数字在矩阵中填入即可。

同时要注意，对于同一行有多个唯一值的情况，每循环一个数，就要将该数从列表中删除，避免Bug。

v_c为逐列检测，n_c为逐个单元格检测。由于每一次填入值都会对其他单元格产生影响，因此我们在主函数中也是用循环，并利用flag来调控。当再也找不到唯一值时，再使用dfs循环。

def solver3(m,n):

    flag=1
    
    while flag==1:
        
        m,n,flag=h_c(m,n)
        m,n,flag=v_c(m,n)
        m,n,flag=n_c(m,n)
    
    l=0
    for i in reversed(range(1,81)):
        if n[i]==0:
            l=i
            break
    if l!=0:
        i=0
        flag=0
        flag=dg(m,n,i,l,flag)

    return m

困难版的运行时间为0.026秒，专家版的运行时间已经压缩到了2.59秒，节省了将近一半的时间。

总结

用时	仅用深度遍历	寻找唯一值+深度遍历	按行列九宫格寻找唯一值+深度遍历
困难版	0.045	0.021	0.026
专家版	5.127	5.465	2.628

可见对于相对简单的数独矩阵，用方法二就能显著提升运算性能，但是对于较困难的矩阵，方法三的提升效果更加显著。

以上均为个人探索的过程，有后续优化的想法，欢迎分享。