Bresenham's line and circle algorithm

今天看了计算机图形学中的画线和画圆算法

Bresenham算法只使用整形加减法和移位

可以说是非常优秀的算法了

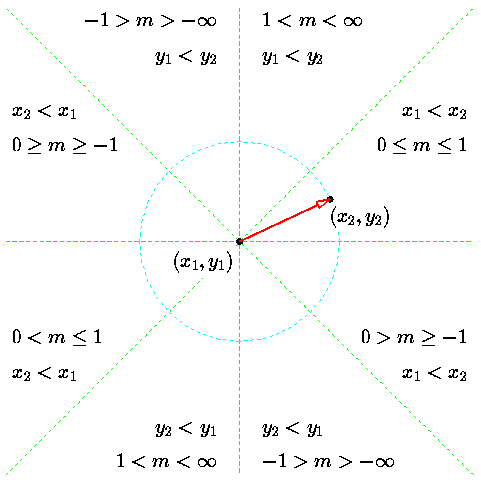
说起“最大位移方向”，就会引入一个坐标概念(octant)。我称它为八等分圆坐标。如下图：

Fig. 1

Bresenham's line and circle algorithm算法中最主要的思想就是

1. 使用了八等分圆坐标来减少运算

2. 使用坐标+0.5的方式来判定下一个绘图点的位置

3. 使用递归的方式做误差的计算和下一次绘图坐标的判断，避免了乘法

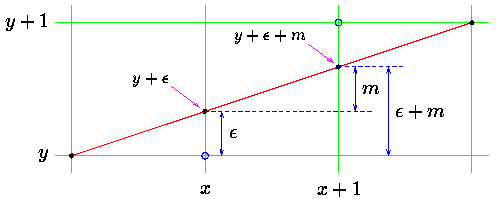
Fig. 2

Bresenham's line算法

这里描述一下在八分之一等分坐标下的算法, 如Fig. 2中

(x, y +ε)的下一个点为(x, y + ε + m)，这里ε为累加误差。

可以看出，当ε+m < 0.5时，绘制(x + 1, y)点，否则绘制(x + 1, y + 1)点。

每次绘制后，ε将更新为新值：
            ε = ε + m ,如果(ε + m) < 0.5 
            ε = ε + m – 1, 其他情况

这里判别条件的  (ε + m) < 0.5

    即 2*(ε + m) < 1

    即 2*(ε + dy / dx) < 1  （由于m = dy / dx）

    即 2*(ε* dx + dy) < dx （同乘以dx）

    令ξ = ε*dx 可得

            ξ = ξ + dy, 如果2*(ξ + dy) < dx
            ξ = ξ + dy – dx, 其他情况
    可以看到，此时运算已经全变为整数了。以下为算法的伪代码：
            ξ ← 0, y ← y1
            For x ← x1 to x2 do
                Plot Point at (x, y)
                If (2(ξ + dy) < dx)
                    ξ ←ξ + dy
                Else
                    y ← y + 1,ξ ←ξ + dy – dx
                End If
            End For

void linev6(Screen &s,
              unsigned x1, unsigned y1,
              unsigned x2, unsigned y2,
              unsigned char colour )
    {
      int dx  = x2 - x1,
          dy  = y2 - y1,
          y   = y1,
          eps = 0;
    
      for ( int x = x1; x <= x2; x++ )  {
        s.Plot(x,y,colour);
        eps += dy;
        if ( (eps << 1) >= dx )  {
          y++;  eps -= dx;
        }
      }
    }

对于其余八等分象限的就不详细展开了

Bresenham's circle算法

Fig. 3

这里描述一下在八分之一等分坐标下的算法, 如Fig. 3中的直角扇形的左上部分45度部分

圆是中心对称的特殊图形，所以可以将圆八等分，则只须对八分之一圆孤求解，其它圆孤可以由对称变换得到

我们求的八分之一圆孤为(0, R) -(R√2,R√2)，可知最大位移方向是x方向

x0 = 0, y0 = R，每次对x自增，然后判断y是否减1，直到x >= y为止(从点(0, R)到圆的八分之一处就有这种情况)。

误差量由Ｆ(x, y) = x^2 + y^2 - R^2给出。


先找递推关系，

若当前d = F(x + 1, y - 0.5) > 0，则y须减1，则下一d值为
    d =  F(x + 2, y - 1.5) = (x + 2)^2 + (y - 1.5)^2 - R^2 = (x + 1)^2 + (x - 0.5)^2 - R^2 + 2x + 3 - 2y + 2 = d + 2x - 2y + 5，

若当前d = F(x + 1, y - 0.5) < 0，则y不变，只有x增1，则下一d值为d = F(x + 2, y - 0.5) = d + 2x + 3。

d的初值，d0 = F(1, R - 0.5) = 1.25 - R，则可以对d - 0.25进行判断

    因为递推关系中只有整数运算，所以d - 0.25 > 0即d > 0.25，这和d > 0等价，所以d取初值1 - R。

void circle(Screen &s,
              unsigned mx, unsigned my,
			  unsigned radius, 
			  unsigned char colour)
{
    int x = 0,y = radius;

    int d = 1-radius;    //起点(0,R),下一点中点(1,R-0.5),d=1*1+(R-0.5)*(R-0.5)-R*R=1.25-R,d只参与整数运算，所以小数部分可省略

    while (y>x)    // y>x 即第一象限的第1区八分圆
    {
        s.Plot(x+mx,y+my,colour);
        s.Plot(y+mx,x+my,colour);
        s.Plot(-x+mx,y+my,colour);
        s.Plot(-y+mx,x+my,colour);

        s.Plot(-x+mx,-y+my,colour);
        s.Plot(-y+mx,-x+my,colour);
        s.Plot(x+mx,-y+my,colour);
        s.Plot(y+mx,-x+my,colour);
		
        if (d<0)
        {
            d=d+2*x+3;
        }
        else
        {
            d=d+2*(x-y)+5;
            y--;
        }
        x++;
    }
}

总结

Bresenham算法：简单图形的扫描转换常用算法

它的思想在于用误差量来衡量点选取的逼近程度。其过程如下：
以平面二维图形的扫描转换为例，设要画的图形方程为F(x, y)=0，要画的区域为[x0, x]（不妨设x方向是最大位移方向，即△x > △y），

则Ｆ(x,y) 也是一个误差度量函数，我们拿离散的点值代入如果大于0则正向偏离，否则负向偏离，等于0的情况比较少，它表示的是不偏离即恰好与真实点重合。

既然x是最大位移方向，那每次对x自增1，相应的y可以选择不增或增1(或-1，具体问题具体分析)，选择的方法就是d = F(x + 1, y ± 0.5)的正负情况进行判断从而选择y的值。

Bresenham's line 讲的最清晰的应该是这个链接

https://www.cs.helsinki.fi/group/goa/mallinnus/lines/bresenh.html

Bresenham's circle 讲的最清晰的应该是这个链接

http://www.cnblogs.com/gamesky/archive/2012/09/03/2668932.html

Bresenham 有个完整版的算法：paper ‘A Rasterizing Algorithm for Drawing Curves’

包含：line, 3dline, circle, ellipse, bezier curve, anti-aliased line, anti-aliased quadratic bezier curve, anti-aliased thick line

http://members.chello.at/~easyfilter/bresenham.html