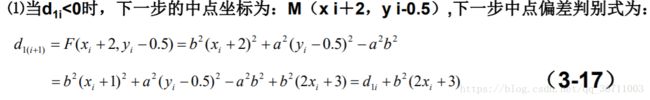计算机图形学学习笔记（上）

第一章 导论

概念

计算机图形学是一门研究如何利用计算机表示，生成，处理和显示的图形的学科。 代表着计算机工业的发展水平。
**图形：**计算机图形学的研究对象。

应用领域：

计算机游戏，计算机辅助设计（CAD or CAM）,计算机艺术，虚拟现实，计算机辅助教学

图形的分类：

1. 基于线条表示的几何图形，如线框图，工程制图，等高线地图等。
2. 基于材质，纹理和光照表示的真实感图形。

图形的表示方法

1. 参数法：参数法是在设计阶段采用几何方法建立图形数学模型
   时，用形状参数和属性参数描述图形的一种方法
2. 点阵法：点阵法是在实现阶段用具有颜色信息的像素点阵来表
   示图形的一种方法，描述的图形常称为图像

相关学科

1. 图像处理：由图像到图像，图像变换(ps)
2. 模式识别：由图像到数学模型，特征提取
3. 计算机图形学：由数学模型到图像，图像显示（3ds max）

图像显示器的发展及工作原理

阴极射线管（CRT）

• 主要是由电子枪，聚焦系统，加速系统，偏转系统，荫罩板，荧光屏组成。
• 由于荧光粉具有余晖特性，电子束停止荧光屏后，荧光屏的亮度并不是立即消失，而是按指数规律衰减，图像会逐渐变暗。
• 为了得到亮度稳定的图像，需要不断地刷新屏幕。当屏幕刷新频率>=60HZ时，人的肉眼就不会感到图像的闪烁。采用的屏幕刷新频率为80HZ。
• 最小刷新频率 = 1/余辉时间

光栅扫描器

1. 画点设备
   光栅扫描器是一个画点设备。，可以看成一个点阵单元发射器，并可控制每个点阵单元的颜色，这些点阵单元被称为像素。
2. 扫描线
   为了能在屏幕上显示整个图形，电子束需要从屏幕的左下角开始，沿着水平方向从左到右匀速扫描，到达第一行的屏幕右端之后电子束立即回到屏幕左端下一行的起点位置，再开始向右端扫描…一直到屏幕的右下角，显示出一帧图像。
3. 荫罩板
4. 位面与帧缓冲
   存储用于刷新的图像信息。储存像素点的颜色值。、
5. 视频控制器

液晶显示器

采用了液晶控制透光度技术来生成图形的显示器。
CRT显示器具有价格低，亮度高，视角宽，使用寿命高的优点。而LCD显示器则有体积小，重量轻，图像无闪烁，辐射低的优点。缺点是视角稍窄，使用寿命短。

第二章 MFC绘图基础

绘图工具类

• CGdiObject类：GDI绘图工具的基类，一般不能直接使用。
• CBitmap：封装了一个GDI位图，提供位图操作的接口。
• CBrush类：封装了GDI画刷，可以选作设备上下文的当前画刷。画刷用于填充图形内部。
• CFont：封装了GDI字体，可以选作设备上下文中的当前字体。
• CPallette：封装了GDI调色板，提供应用程序和显示器之间的颜色接口。
• CPen：封装了GDI画笔，可以选作设备上下文的当前画笔。画笔是用于绘制图形边界线

映射模式

1. 设置映射模式函数

virtual int SetNMapMode(int nMapMode)

返回值：原映射模式，用宏定义值来表示

2. 设置窗口范围函数

virtual CSize SetWindowExt(int cx,int cy);
virtual CSize SetWindowExt(SIZE size);

参数：cx窗口x范围的逻辑坐标,cy窗口y范围的逻辑坐标;size 是窗口的SIZE或CSIZE对象。
返回值：原窗口范围内的CSIZE对象。
3. 设置视区范围函数

virtual CSize SetViewportExt(int cx,int cy);
virtual CSize SetViewportExt(SIZE size);

参数：cx视区x范围的逻辑坐标,cy视区y范围的逻辑坐标;size 是视区的SIZE或CSIZE对象。
返回值：原窗视区范围内的CSIZE对象。

4. 设置窗口原点函数

CPoint SetWindowOrg(int x,int y);
CPoint SetWindowOrg(POINT point);

参数：x,y是窗口新原点坐标;point是窗口新原点的POINT结构或者CPoint对象。
返回值：原窗口原点的CPoint对象。
5. 设置视区原点函数

virtual CPoint SetWindowOrg(int x,int y);
virtual CPoint SetWindowOrg(POINT point);

参数：x,y是视区新原点坐标;point是视区新原点的POINT结构或者CPoint对象。
返回值：原视区原点的CPoint对象。

注意点：窗口可以理解为一种逻辑坐标下的句型区域，而视区是设备坐标系下的矩形区域。根据窗口和视区的大小可以确定x方向和y方向的比例因子。

设置x轴正向向右，y轴正向向上，客户区中心为中心原点。

pDC->setWindowExt(rect.Width(),rect.Height());
pDC->setViewportExt(rect.Width(),-rect.Height());
pDC->setViewportOrg(rect.Width()/2,rect.Height()/2);

把一个100200的窗口中的图形显示到200px200px的视区中
窗口映射到视区中，y方向的比例为1（不变），x方向的比例为2 （放大2倍）。
一个逻辑单位在y方向映射为一个像素，x方向都映射为2个像素

pDC->SetMapMode(MM_AISOTROPIC);
pDC->SetWindowExt(100,200);
pDC->SetViewportExt(200,200);

保持X轴正向向右不变，当Y轴正向向下时 SetViewportOrg(x, y);与
SetWindowOrg(-x, -y);等价
当Y轴正向向上时 SetViewportOrg(x, y);与SetWindowOrg(-x, y);等价

使用GDI对象

Cpen NewPen,*OldPen;
NewPen.CreatePen(PS_SOLID,1,RGB(0,0,255));//创建蓝色画笔
OldPen=pDC->SelectObject(&NewPen);//选入对象
...
pDC->SelectObject(OldPen);//保存原画笔
NewPen.DeleteObject();

第三章 基本图形的扫描变换

直线的扫描变换

中点Bresenham算法原理

设当前屏幕上最逼近直线的像素点为Pi（xi,yi），下一个像素点Pi+1（xi+1,yi+1）相较于前一个像素点的坐标每次在主位移方向上+or-1,另一个方向上是否+or-1取决于中点偏差判别式的值。
若直线斜率绝对值<=1，直线在x方向上变化快，以x为主位移方向。否则，以y为主位移方向。

构造中点误差项

从Pi（xi,yi）点出发选择下一像素时，需将Pu和Pd的中点M（xi+1,yi+0.5）代入隐函数方程，构造中点误差项di。
di = F（xi+1,yi+0.5） = yi+0.5-k(xi+1)-b

当di < 0时，中点M在直线的下方，Pu点离直线距离更近，下一像素点应选取Pu,即y向上走一步；di = 0时，选取两点均可。否则，选取Pd点,y方向上不移动。

因此

递推公式

1. 中点误差项的递推公式

2. 中点误差项的初始值
   直线的起点坐标为P0（x0,y0），x为主位移方向，因此第一个中点是M（x0+1,y0+0.5），相应的di的初始值为

算法实现

void Bresenham(int x0,int y0,int x1,int y1){
	int dx = x1-x0,dy = y1-y0;
	int x = x0,y = y0;
	double k = 1.0*dy/dx;
	double d;
	//绘制斜率k为0<=k<=1的直线 
	if(k >= 0 && k <= 1.0){
		//设置直线段的颜色 
		COLORREF clr = RGB(255,0,0); 
		d = 0.5-k;
		//不包括中点 
		for(x = x0;x < x1;x++){
			pDC->SetPixel(Round(x),Round(y),clr);
			if(d < 0){
				y++;
				d += 1-k;
			}
			else{
				d-=k;
			}
		}
	}
}

园的扫描变换

算法原理

本算法是考虑45°的圆弧及第一象限x在[-,R/sqrt(2)]的1/8圆弧、

构造中点误差判别式

递推公式

（1）当di <0时，下一中点的坐标为：M（xi+2,yi-0.5）。所以下一步中点偏差判别式为：

（2）di >= 0时，下一中点的坐标为：M（xi+2,yi-1.5）。所以下一步的中点误差判别式为：

中点偏差判别式的初始值

算法实现

//画中点的Bresenham算法
void CTestView::MBCircle(double R,CDC *pDC){
	double d;
	d = 1.25-R;
	int x = 0,y = R;
	for(x = 0; x <= y;x++){
		//调用八分法画圆子函数 
		CirclePoint(x,y,pDC);
		if(d < 0){
			d += 2*x+3; 
		}
		else{
			d += 2*(x-y)+5;
			y--;
		}
	}
}

void CTestView::CirclePoint(int x,int y,CDC *pDC){
	//圆心坐标
	CP2 pc = CP2((p0.x+p1.x)/2.0,(p0.y+p1.y)/2.0);
	//定义圆的边界颜色
	COLORREF clr = RGB(0,0,255);
	pDC->SetPixelV(Round(x+pc.x),Round(y+pc.y),clr);
	pDC->SetPixelV(Round(y+pc.x),Round(x+pc.y),clr);
	pDC->SetPixelV(Round(y+pc.x),Round(-x+pc.y),clr);
	pDC->SetPixelV(Round(x+pc.x),Round(-y+pc.y),clr);
	pDC->SetPixelV(Round(-x+pc.x),Round(-y+pc.y),clr);
	pDC->SetPixelV(Round(-y+pc.x),Round(-x+pc.y),clr);
	pDC->SetPixelV(Round(-y+pc.x),Round(x+pc.y),clr);
	pDC->SetPixelV(Round(-x+pc.x),Round(y+pc.y),clr);
}

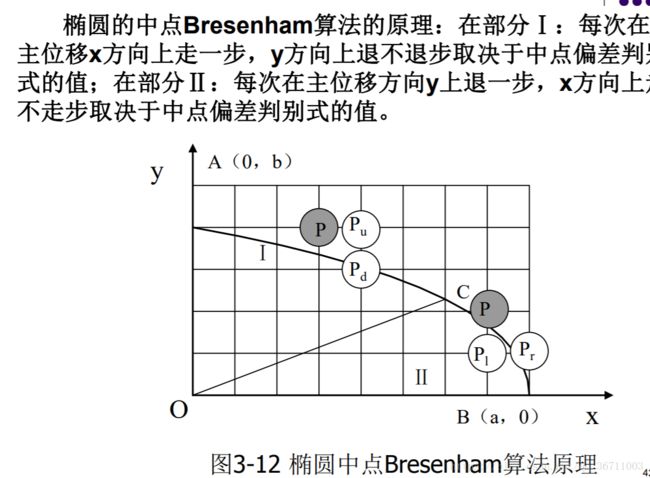
椭圆的扫描变换

算法原理

构造上半部分I的中点偏差判别式

上半部分I的递推公式

中点偏差判别式的初值

下半部分II的中点偏差判别式

下半部分II区域递推公式

中点偏差判别式的初值：

算法实现

void CTestView::MBEllipse(CDC *pDC){
	int x,y,a,b;
	double d1,d2;
	x = 0,y = b;
	d1 = b*b+a*a*(-b+0.25);
	EllipsePoint(x,y,pDC);
	//椭圆前半段 
	while(b*b*(x+1) 0){
		if(d2 <0){
			d2+=b*b*(2*x+2)+a*a*(-2*y+3);
			x++;
		}
		else{
			d2 += a*a*(-2*y+3);
		}
		y--;
		EllipsePoint(x,y,pDC);
	}
}
//四分法画椭圆子函数 
void CTestView::EllipsePoint(double x,double y,CDC *pDC){
	//椭圆中心坐标
	CP2 pc = CP2((p0.x+p1.x)/2.0,(p0.y+p1.y)/2.0);
	//定义椭圆的颜色
	COLORREF clr = RGB(0,0,255);
	pDC->SetPixelV(Round(x+pc.x),Round(y+pc.y),clr);
	pDC->SetPixelV(Round(-x+pc.x),Round(y+pc.y),clr);
	pDC->SetPixelV(Round(x+pc.x),Round(-y+pc.y),clr);
	pDC->SetPixelV(Round(-x+pc.x),Round(-y+pc.y),clr); 
}

反走样技术

• 走样：由离散量表示连续量而引起的失真称为走样
• 反走样：用于减轻走样现象的技术。

第四章：多边形填充

多边形的扫描转换

多边形的表示

（1）顶点表示法

• 是用多边形的顶点序列来描述
• 优点：特点是直观，占内存少，易于进行几何变换
• 缺点：没有明确指出哪些像素在多边形内，所以不能直接进行填充，需要对多边形进行扫描转换。

（2）点阵表示法

• 是用多边形覆盖的像素点集来描述。内部像素具有一种颜色，边界像素和外部像素具有另外的颜色。
• 优点：是便于直接确定实面积图形覆盖的像素点，是多边形填充所需要的表示形式。
• 缺少了多边形顶点的几何信息。

（3）多边形的扫描变换

将多边形的描述从顶点表示法变换到点阵表示法的过程，叫做多边形的扫描转换。即从多边形的顶点信息出发，求出多边形内部的各个像素点信息。

多边形的填充

一般原理：

1. 从屏幕上的扫描线出发，首先确定多边形覆盖的扫描线条数（y = ymin-ymax）
2. 对每一条扫描线，计算扫描线与多边形边界的交点区间（xmin-xmax），然后再将该区间内的像素赋予指定的颜色。
   在扫描线从多边形顶点的最小值ymin到多边形顶点的最大值ymax移动过程中，重复上述工作，就可以完成多边形的填充。

区域填充

• 对于用点阵表示的多边形，内部像素具有一种颜色，边界像素和外部像素具有另外的颜色，可以使用区域填充法。
• 区域是指一组相邻而又具有相同属性的像素，可以理解为多边形的内部。
• 种子填充算法是从给定的种子位置开始，按填充颜色点亮种子的相邻像素知道颜色不同的边界像素为止。种子填充算法主要有4邻接点算法和8邻接点算法。

有效边标填充算法

填充原理

按照扫描线从小到大的移动顺序，计算当前扫描线与多边形各边的交点，然后按照交点用指定的颜色点亮区间内的所有像素，完成填充工作。

填充步骤

1. 求交：首先用每一条扫描线对多边形所有的边求交，建立交点表，水平边跳过。
2. 排序：对交点进行排序，统一扫描线上的交点按X坐标排序，对于不同扫描线上的交点，按照Y坐标排序。
3. 填充：然后将每一对交点间的所有像素置新值。

边界像素处理原则：下闭上开，左闭右开

有效边和有效边表

1. 有效边
   多边形内部与当前扫描线相交的边称为有效边。
   - 某条有效边和不同扫描线的交点y坐标变化：yi+1 = yi + 1;
   - 设有效边的斜率为k。假定有效边与当前扫描线yi的交点为（xi,yi），则有效边与下一条扫描线yi+1的交点为（xi+1,yi+1）。
   - 其中yi+1 = yi + 1;xi+1 = xi + 1/k = xi + dx/dy;
2. 有效边表
   把有效边按照与扫描线交点x坐标递增的顺序放入一个链表中，称为有效边表，有效边表的结点如下所示：

x	ymax	1/k	next

有效边的数据结构定义如下：

//有效边类 
class AET{
	public:
		AET();
		virtual ~AET();
		double x;
		int ymax;
		double k;
		AET *next;
};

边表

有效边表给出了扫描线和有效边交点坐标的计算方法，但是没有给出新边出现的位置坐标，为了确定在哪条扫描线上插入了新边，就需要构造一个边表，用以存放扫描线上多边形各条边出现的信息。

边表的表示方法：

• 把待填充的多边形的各边放入ET（边表）
• 边表为一个纵向扫描线链表。
• 链表的每个结点称为桶，对应和多边形相交的每一条扫描线。

桶的数据结构定义如下：

class Bucket{
	public:
		Bucket();
		virtual ~Bucket();
		//扫描线 
		int ScanLine();
		//桶上的边表指针
		Bucket *next;
}; 

将每一边放入与该边最小y坐标相对应的桶中。

x|ymin	ymax	1/k	next

算法流程

1. 取当前扫描线y为边表中第一个非空存储桶的y值
2. 有效边表AET设为空
3. 对当前扫描线执行下列步骤，直到边表ET和有效边表AET都变为空为止。
   • [a] 取出ET中当前扫描线y所对应的存储桶中所有的边，并插入有效边表AET中，AET中的各边按照Xmin值（当Xmin相等时，按照1/k递增方向排序）。
   • [b] 将AET中满足y = Ymax的边删去。（下闭上开）
   • [c] 将AET中的边两两一次配对，即1,2边为一对，3,4边为一对，一次类推。当前扫描线y与每一条边的交点正好是（x,y），填充每对交点之间的部分。（左闭右开）
   • [d] 将AET剩下的每一条边的x都变为x + 1/k。
   • [e] 将当前的扫描线的坐标值y累加1。即y = y + 1。重复以上步骤。

边缘填充算法

原理：求出多边形的每条边与扫描线的交点，然后将交点右侧的所有像素颜色全部取为反色。按任意顺序处理完多边形所有边后，就完成了多边形填充任务。

区域填充算法

原理：用点阵表示的多边形区域，如果其内部像素具有同一种颜色，而边界像素具有另一种像素，可以使用种子填充算法进行填充。种子填充算法是从区域内任意一个种子像素开始，由内向外将填充色扩充到整个多边形区域。

四连通域

从多边形区域内任意一个种子像素点出发，通过访问其左上右下这4个邻接点可以遍历区域内所有像素。

八连通域

从多边形区域内任意一个种子像素点出发，通过访问其左，左上，上，右上，右，右下，下，左下这8个邻接点可以遍历区域内所有像素点。

种子填充算法原理

先将种子像素入栈。种子像素为栈底像素，如果栈不为空，执行如下三步：

1. 栈顶像素出栈
2. 按填充色绘制出栈像素
3. 按左上右下顺序搜索与出栈像素相邻的4个像素，若该像素的颜色不是边界色且未置成填充色，则把该像素入栈；否则丢弃该像素。

扫描线种子填充算法

先将种子像素入栈，种子像素为栈底像素，如果栈不为空，执行如下4步：

1. 栈顶像素出栈
2. 沿扫描线对出栈像素的左右像素进行填充，直至遇到边界像素为止。及每出栈一个像素，就对区域内包含该像素的整个连续区间进行填充。
3. 同时记录该区间，将区间最左端像素记为Xleft，最右端像素记为Xright.
4. 在区间[Xleft,Xright]中检查与当前扫描线相邻的上下两条扫描线的有关像素是否全为边界像素或已填充元素，若存在非边界且未填充像素，则把为填充区间的最右端像素取作种子像素入栈。