字符串查找问题——KMP算法
问题描述:给定一个文本串text和模式串pattern,从文本串text中找出模式串pattern第一次出现的位置
1.最基本的字符串匹配算法,暴力求解(时间复杂度m*n)
实现思路:遍历text串和pattern串,使用两个变量i,j,当text[i+j]相等时j++,不等时,j直接回溯到0即可,直到最后。
实现方法如下:
int bruteforceSearch(char* text, char* pattern) {
int i = 0;//用于遍历text字符串,表示在text中的位置
int j = 0;//用于遍历pattern字符串
//求两个字符串的
int size = (int)strlen(text);
int psize = (int)strlen(pattern);
while (i<size&&j<psize)
{
if (text[i+j]==pattern[j])//向后比较
{
j++;
}
else//不匹配,查找下回一个位置
{
i++;
j = 0;
}
}
if (j>=psize)
{
return i;
}
return -1;
}
注意:这里返回的i是所求位置的前一个位置下标,没有匹配则返回-1
2.KMP算法,是对暴力算法的一种改进(时间复杂度是线性的)
实现思路:其实KMP算法相当于是对暴力算法的一个改进,主要是在j回溯时,不将j置为0,而是将置为next[j](这个next数组后面我会详细说明他的求法,这个也是KMP的核心)。
如图:
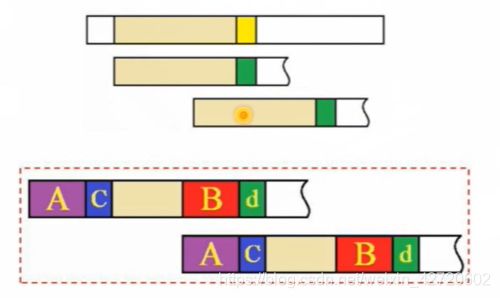
假设当前i指向换色区域,j指向绿色区域,如果text[i]!=pattern[j],j就需要回溯,如果A区域和B区域相等,设紧接着text[i]前面存在一个区域H,使得H=B,因为两个串是从前往后一次匹配,所以这个H一定存在,又因为A=B,所以A=H,所以当j回溯时只需要将j回溯到A区域的下一个位置,也就是上图中的C了。
next数组的定义和作用:
将上图中A—B看成一个字符串,则称A为这个串的前缀串,B为这个串的后缀串,当前j指向的是区域B的下一个位置,next[j]=A的长度或者B的长度。当j回溯时,需要回溯的值恰好是next[j],也就是j=next[j];
next数组的求法:假设我们已知next[j]=k,求next[j+1],也就是求一个递推关系。
分两种情况:
①pattern[j]=pattern[k]时:next[j+1]=next[j]+1(因为pattern[j]=pattern[k],A=B)
如图:
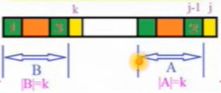
②pattern[j]!=pattern[[k]时:
如图:

设h=pattern[k],如果pattern[h]=pattern[j]的话,pattern[j+1]=h+1(原因:,根据next的特性,前缀串和后缀串相等,所以区域1=区域3,区域3=区域2,则区域1=区域2);如果还是不等,再接着上述重复上述过程即可求出pattern[j+1]
实现代码如下(求next数组):
void CalcNext(char* p, int next[]) {
int nLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j<nLen-1)
{
//此刻,k即next[j-1],且p[k]表示前缀,p[j]表示后缀
//注:k==-1表示未找到k前缀与k后缀相等,首次分析可先忽略
if (k==-1||p[j]==p[k])
{
++k;
++j;
next[j] = k;//起初next[j]=k, next[j+1]=k+1 =>next[j+1]=next[j]+1
}
else//p[j]与p[k]失配,则继续递归索引p[next[k]]
{
k = next[k];
}
}
}
这里解释一下k=next[k],这句代码就是上面的pattern[k]!=pattern[j]时的做法,就可以看成上面的求h的过程,就一直向左缩小k的值,知道找到pattern[k]=pattern[j]为止。
求出next数组后,后面找位置就相对比前面简单一些了,和包,暴力算法的思路一样,依次遍历两个字符串,当text[i]!=pattern[j]时,j=next[j]即可。
实现代码(求具体的位置):
int KMP(int n,char* pattern,int* next,char* text) {
int ans = -1;
int i = 0;
int j = 0;
int pattern_len = strlen(pattern);
while (i<n)
{
if (j == -1||text[i]==pattern[j])
{
i++;
j++;
}
else
j = next[j];
if (j==pattern_len)
{
ans = i - pattern_len;
break;
}
}
return ans;
}
注意:这里返回的ans是所求位置的前一个位置下标,没有匹配则返回-1
KMP算法的改进:
只在计算next数组中做了改进,当pattern[j]==pattern[k]时,pattern[j]=next[k](原因:当pattern[j]!=text[i]时,pattern[k]!=text[i],由next数组前缀串等于后缀串的性质得到,pattern[j]=next[k])
具体实现如下:
void CalcNext1(char* p, int next[]) {
int nLen = strlen(p);
next[0] = -1;
int k = -1;
int j = 0;
while (j < nLen - 1)
{
//此刻,k即next[j-1],且p[k]表示前缀,p[j]表示后缀
//注:k==-1表示未找到k前缀与k后缀相等,首次分析可先忽略
if (k == -1 || p[j] == p[k])
{
++k;
++j;
//改进的地方,如果p[j+1]=p[k],那么j回溯的位置就不用移到k位置,因为p[k]肯定不等于text[i]
if (p[j]==p[k])
{
next[j] = next[k];
}
next[j] = k;//***起初next[j]=k, next[j+1]=k+1 =>next[j+1]=next[j]+1
}
else//p[j]与p[k]失配,则继续递归索引p[next[k]]
{
k = next[k];
}
}
}
因为所需要的图片难找,所以我的叙述过程中所用到的图片是从视频中扣下来的,可能有些模糊,请谅解!还有,我也是初学者,叙述过程中出现的错误或者有什么自己的看法,欢迎留言讨论交流。