几何检测

概述

几何检测主要相交性检测，这里的内容大体上是根据《3D数学基础-图形与游戏开发》这本书来的，对于这本书来说，这一部分看完了后面内容就不看了，因为后面讲的太空泛了，有点像一本绝世武功的目录一样，看似很强，其实没什么卵用。

1.2D隐式直线上的最近点

问题描述：
直线p * n = d，对于任意点q，找出直线上距离q最短的点q’

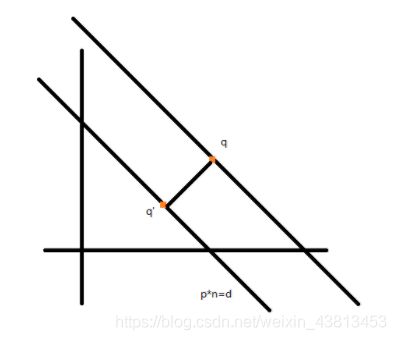
同高中解析几何简单粗暴的公式不同，这里面的算法都是基于向量来计算的。
如图所示，对于q来说，我们做另一条平行于原直线的直线，p’ * n’ = d’，显然有q * n = d’
于是两条直线分别为：
$$p\ast n=d$$
$$p\ast n=q\ast n$$
则其距离为d-q * n，但是我觉得是不是少除了个n的模长，这里的n应该是单位向量才正确！
然后交点就为
q’ = q + (d - q * n)n
如果n不是单位向量的话，那么距离应该等于
$$\frac{d-q\ast n}{|n|}$$

2.参数射线上的最近点

问题描述：
参数射线R：$p(t)=p_{org}+td$
d为单位向量，参数t在0到l之间变换，l是直线的长度。对于定点q，我们想要在射线R上求出距离q最近的点q’.

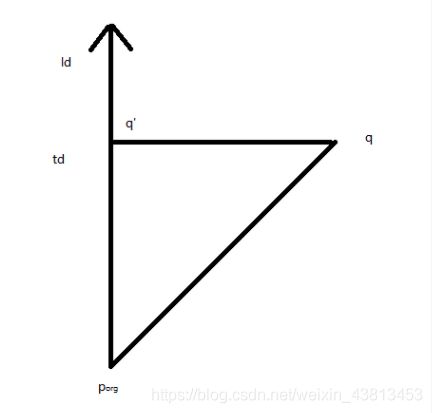
这个问题的求解要比上面的简单一点，本质上是一个向量的投影问题。
设$v=q-p_{org}$,则$v\ast d=td$
这样能得出q在直线上的投影向量，我们能解出来t，然后带回到公式即可，有：
$q^{\prime }=p_{org}+(d\ast (q-p_{org}))d$

3.平面上最近的点

平面和直线的表达式其实是一样的，也是
$$p\ast n=d$$
最后得到的表达式其实也是一样的，但是推导过程有差别，如下图所示，设有平面pn=d，n为单位法向量，q为不在平面上的任意一点，p为其在平面上的投影

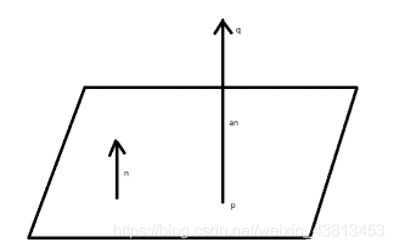
有
p + an = q
(p+an)n = qn
pn+ann = qn
d+a=qn
a=qn-d
因此有q’ = q+an = q + (d-qn)n，也就是点到直线的最近点的公式一样。

4.圆或球上的最近点

对于球心为c，半径为r的球，球外一点q，在球上求一点q’，使得q’距离q最短。
我们设向量d = c-q，
那么有$b=d\ast \frac{|d|-r}{|d|}$
然后有q’ = q+b
则$q^{\prime }=q+d\ast \frac{|d|-r}{|d|}$

5.2D隐式直线的相交性检测

这个检测方法简单粗暴，直接联立两个方程求解即可，解的个数应对着相交、平行、重合这三种情况。

6.3D中两条射线的相交性检测

3D直线的隐式方程实际上是两个屏幕的交线，这种方式当然也可以联立四个方程，同上面一样进行求解，但这里我们讨论参数方程的情况。
设两条直线的参数方程为：
$$r_1(t_1)=p_1+t_1{d}_1$$
$$r_2(t_2)=p_2+t_2{d}_2$$
这个具体的推导还是很秀的，让我推导我肯定不会，书上联立$r_1(t_1)=r_2(t_2)$,然后经过一波天秀的推导，得到了下面的解：
$$t_1=\frac{((p_2-p_1)x{d}_2)\ast (d_{1}x{d}_2)}{|d1xd2{|}^2}$$
$$t_2=\frac{((p_2-p_1)x{d}_1)\ast (d_{1}x{d}_2)}{|d1xd2{|}^2}$$
当上面式子的分母等于0的时候，对应的是两条射线平行或者重合，其他情况下$p_1(t_1)和p_2(t_2)$是距离最近的点，如果距离等于零，则表示相交，否则则两直线属于异面直线。

7.射线和平面的相交检测

射线的参数方程定义为：$p(t)=p_0+td$,平面方程为p * n = d.
相交性检测比前面求距离的要简单的多，因为不需要很多的几何理解，只需要联立求交点就行，求得到，就有交点，求不到，就没交点，把上面的公式联立起来，得到解
$$t=\frac{d-p_0\ast n}{d\ast n}$$
同样的，分母为0，则没交点。

8.AABB包围盒和平面的相交性检测

AABB包围盒有8个顶点，我们把它代入到p* n= d这个平面方程中去，然后如果八个点全部小于或者大于d则不相交，否则相交，书上有优化的办法，可以不用求所有的八个点，但是我感觉已经没什么必要了，没什么明显的复杂度改进没必要加大算法难度。

9.三个平面的相交性检测

也是一个解方程组的问题，三个平面是否相交于一点，如何求该点，首先三个平面分别为：
$$p{n}_1=d_1$$
$$p{n}_2=d_2$$
$$p{n}_3=d_3$$
然后联立可以求得：
$$p=\frac{d_1(n_{3}x{n}_2)+d_2(n_{3}x{n}_1)+d_3(n_{1}x{n}_2)}{(n_{1}x{n}_2)\ast n_3}$$
怎么推导的就别管了，头发要紧。

10.射线和圆/球的相交性检测

这个检测很有技巧性，比起直接联立方程来说，这种方法的实现难度也同时低很多。

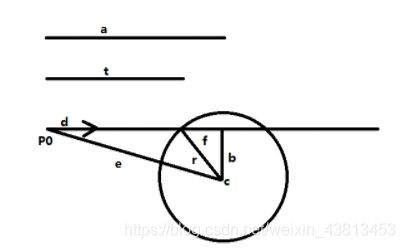
这个几何体的构造就挺有东西的，直线的方程是$p(t)=p_0+td$，d为单位向量，圆的圆心为c，半径为r。
我们的目的是求出来t，然后代入到直线方程就可以得到交点的信息。
t=a-f
a=(c-p0)d//P0C在直线上的投影
对于f，有
$$f^2+b^2=r^2$$
$$b^2=e^2-a^2$$
联立可解得
$$f=\sqrt{r^2-e^2+a^2}$$
则有
$$t=a-\sqrt{r^2-e^2+a^2}$$
若根号内为负值，则不相交。

11.两个圆/球的相交性检测

对于静止的两个球来说，求是否相交是非常简单的，只需要判断他们距离的平方和两个半径的平方和的大小即可。

12.球和AABB的相交性检测

只需要判断距离球心最近的包围盒的距离球心的距离和求半径的关系即可。

13.球和平面的相交性检测

只需要判断球心和平面的距离和球半径的关系即可。

14.射线和三角形的相交性检测

这里涉及到三角形的重心坐标系，三角形平面上每个点都可以用三个顶点的线性组合来表示，这个坐标就是三角形的线性坐标，假设我们已知三角形的三个顶点，以及三角形平面上一点p的坐标，设p在三角形重心坐标系的坐标为(b1,b2,b3)则有
$$p_x=b_1{x}_1+b_2{x}_2+b_3{x}_3$$
$$p_y=b_1{y}_1+b_2{y}_2+b_3{y}_3$$
$$b1+b2+b3=1$$
当b1=b2=b3=$\frac{1}{3}$的时候，我们认为p点是三角形的重心坐标，由上面的式子，可以解得：
$$b_1=\frac{(p_y-y_3)(x_2-x_3)+(y_2-y_3)(x_3-p_x)}{(y_1-y_3)(x_2-x_3)+(y_2-y_3)(x_3-x_1)}$$
$$b_2=\frac{(p_y-y_1)(x_3-x_1)+(y_3-y_1)(x_1-p_x)}{(y_1-y_3)(x_2-x_3)+(y_2-y_3)(x_3-x_1)}$$
$$b_3=\frac{(p_y-y_2)(x_1-x_2)+(y_1-y_2)(x_2-p_x)}{(y_1-y_3)(x_2-x_3)+(y_2-y_3)(x_3-x_1)}$$
我们判断三角形和射线相交的方法如下：
1.计算射线和三角形平面的交点
2.计算交点的重心坐标
3.如果重心坐标某一分量小于零，则其在三角形外，没有交点，否则有交点，交点可以通过重心坐标乘上三角形顶点坐标获得。

15.两个AABB的相交性

如果一个包围盒x最小值都大于另一个包围盒x的最大值，则不相交，按照这个理论，有六种纬度去判断，只要有一种不满足，则其不相交。

16.后记

书上介绍的比我这个是要复杂一点的，还包括了动态的相交检测，这里我没涉及到，如果有需要用到的时候再看吧，也许那会是下辈子。。。