论文:https://arxiv.org/pdf/2007.11823.pdf
代码:https://github.com/megvii-model/WeightNet
这是香港中文大学和旷视科技的最新工作,提出了一个即插即用并可以有效涨点的网络WeightNet,作者也指出,该网络是受了最近关注度较高的 conditional network 的启发。
Conditional network (或者叫做 Dynamic network)最近受到广泛关注。作者分析了 Conditional network 和 SENet 的联系,二者都包括两个步骤:第1步,得到一个 attention activation vector,然后 SENet 利用该向量给特征通道分配权重,CondConv 是给一系列卷积核分配权重 (a mixture of expert weights)。两者一直被视作完全不同的方法,作者提出一个问题:“Do they have any correlations ?”
为此,作者设计了WeightNet,首先需要了解一个概念:Grouped FC。 普通的FC操作可以理解 为一个矩阵运算 \(Y=WX\) ,如下图(a)所示。在此基础上添加分组操作的话,就成为了图(b) 所示的 Grouped FC。在图中,FC运算分为了 \(g\) 组,每一组的输入为 \(i/g\) ,输出 为 \(o/g\) 。这是联系 WeightNet 和 CondConv 的关键操作。
同时,作者给出一个定义:设输入特征为 \(X\in R^{C\times H\times W}\),输出特征为\(Y\in R^{C\times H\times W}\),卷积权值可以看作 \(W \in R^{C\times C\times k\times k}\)。这样卷积可以看作 \(Y_c=W_c * X\)。
1. Rethinking CondConv
CondConv 第一步是得到权重向量 \(\alpha\) ,这个步骤可以这样描述:\(\alpha=\sigma(W_{fc1}\times \frac{1}{hw}X)\) ,这里 \(W_{fc1}\in R^{m\times C}\), \(\alpha\in R^{m\times1}\)。
第二步,为卷积分配权重,可以理解为:\(W'=W^T\times \alpha\),这里 \(W\in R^{m\times CCkk}\)
2. Rethinking SENet
SENet 第一步也是得到权重向量\(\alpha\),可以这样描述:\(\alpha = \sigma(W_{fc2}\times \textrm{ReLU}(W_{fc1}\times \frac{1}{hw}X))\) 。两个全连接层中间有降维,reduction ratio 为 16。
第二步,为 feature map 的各个通道分配权重,整个过程可以理解为:\(Y_c=(W'_c\cdot \alpha_c) * X\)。这可以理解为一个特殊的 Grouped FC,输入是 \(C\),输出是 \(C\times C\times k\times k\),只是分为 \(C\) 组。
3. WeightNet
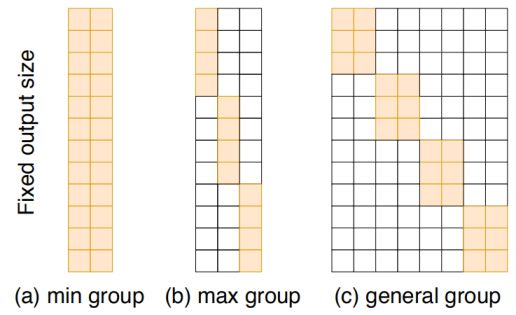
作者提供了一个图来说明 WeghtNet, SENet 和 CondConv 的区别与联系,如下所示。三个操作都输出同样的 \(C\times C\times k \times k\)卷积矩阵,但是 图(a) 为只有一组(CondConv),图(b)为有C组(SENet),图(c)为自定义组数(WeightNet)
作者在 WeightNet 中引入了参数 \(M\) 和 \(G\)。 权重向量 \(\alpha\) 为一个 \(M \times C\)维的向量。但是因为维度过高,使用了两个全连接层处理: \(\alpha = \sigma(W_{fc2}\times W_{fc1} \times \frac{1}{hw}X)\),丙个全连接层,reduction ratio 为16。
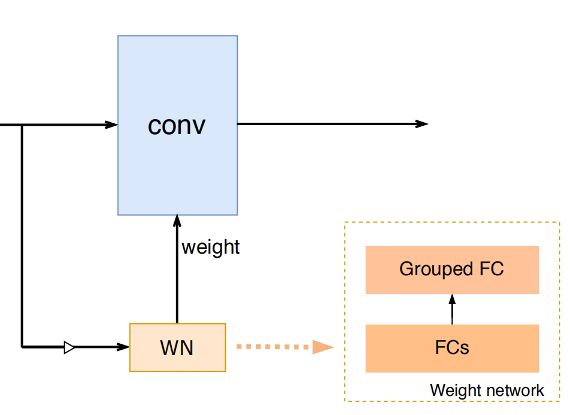
在第二步里,建立 Grouped FC,输入为 \(M\times C\),输出为 $\times C\times C\times k \times k $,分组数量为 \(G\times C\)。总体的图示如下:
需要注意的是,数据训练是要分batch的,因此,输入的X维度为\((B, C, H , W)\),对其进行reshape 得到 \((1, B\times C, H, W)\),然后对生成的 \(W\) 进行reshape得到 \((B, C, C, k, k)\),然后采用组卷积的形式进行计算。 CondConv 也采用了这样的处理方式。
实验部分建议参考一下论文,这里不详细介绍了。