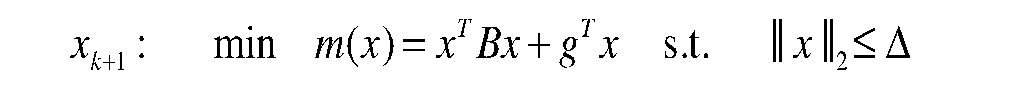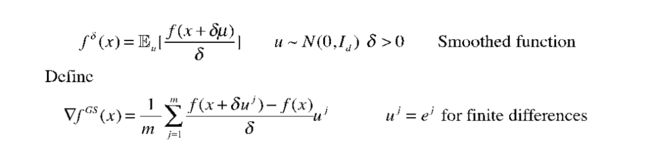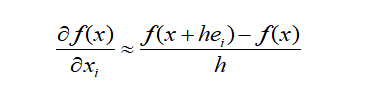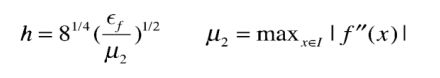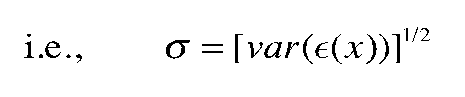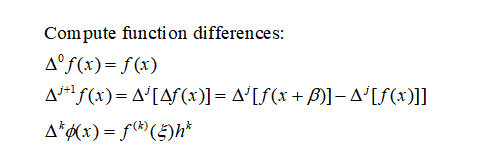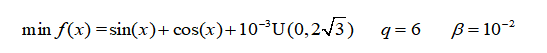冯·诺伊曼奖得主Jorge Nocedal:增强学习中零阶优化方法及其应用(附演讲视频和PPT)
2020 北京智源大会
本文属于2020北京智源大会嘉宾演讲的整理报道系列。北京智源大会是北京智源人工智能研究院主办的年度国际性人工智能高端学术交流活动,以国际性、权威性、专业性和前瞻性的“内行AI大会”为宗旨。2020年6月21日-24日,为期四天的2020北京智源大会在线上圆满举办。来自20多个国家和地区的150多位演讲嘉宾,和来自50多个国家、超过50万名国内外专业观众共襄盛会。
2020年6月22日上午,在第二届北京智源大会全体会议上,冯·诺依曼理论奖得主、美国西北大学教授Jorge Nocedal做了名为《Zero-Order Optimization Methods with Applications to Reinforcement Learning》的主题演讲。
Jorge Nocedal,美国西北大学教授,曾在非线性优化、应用数学和运筹学等领域获得无数奖项。2009年获查尔斯·布罗伊登奖;2010年,他还被评为美国工业和应用数学学会院士;2012年获乔治·B·丹齐格奖;2017年,被授予冯·诺依曼理论奖。2020年当选美国工程院院士。Nocedal主要的研究方向为确定性和随机性设置中的非线性优化,他目前进行的算法和理论研究的动机源于图像、语音识别、推荐系统和搜索引擎中的非线性优化问题。
Nocedal在演讲中指出,在函数优化的过程中,我们通常可以使用梯度下降的方法来获得目标函数的最值,但其实这需要依赖许多最值搜索的“运气”,其中包括:良好的初始化、步长、迭代方向计算的精度、搜索空间的结构等,但是在深度学习中,尤其是增强学习中,这些“运气”并不一定可以满足,那么我们如何通过其他的方法来做深度学习中目标函数的优化呢,本次会议中Nocedal给我们分享了他的独到思路——零阶优化。所谓零阶优化算法即不利用一阶导数信息,在一定次数的抽样基础上,拟合目标函数的最值。零阶优化方法通过对目标函数逼近或对目标函数加罚函数的方法,将约束的优化问题转换为非约束的优化问题。
整理:智源社区 钱小鹅
一、函数优化与深度学习
深度神经网络主要基于两个核心思想:其一是适合生成表示的预测函数结构,其二是在合适的空间中帮助寻找到合适的预测函数的反向传播算法。这里,反向传播算法通常意味着两件事:1)可以进行链式微分;2)可以使用梯度下降的方法进行优化。然而,优化过程中使用梯度下降法并不一定保证获得的解能够收敛到我们所期望的最小值。如下图所示,我们发现在优化过程中使用梯度下降方法,如果想要获得我们期望的结果,其依赖的条件有很多,比如:初始值、迭代步长的选择、迭代方向的计算等。
图1: 从不同初始值开始,非凸优化将得到不同的优化结果
上述我们提到的对函数优化的疑问,不少知名的数学界学者同样也对此表示怀疑,例如:
Minsky 1961
I doubt that in any one simple mechanism, e.g., hill-climbing, will we find the means to build an efficient and general problem-solving machine.(我怀疑,在任何一个简单的机制中,例如爬山,我们是否能找到建立一个高效和通用的问题解决机制的方法。)
Minsky and Papert 1998
If we can detect relative improvement, then "hill-climbing" may be feasible, but its use requires some structural knowledge of the search space. And unless this structure meets certain conditions, hill-climbing may do more harm than good.(如果我们能检测到相对改进,那么爬山是可行的,但使用它需要搜索空间的结构知识。除非这种结构满足某些条件,否则弊大于利。)
事实上,在不同的搜索空间结构情况下,梯度下降法获得的效果不尽相同,甚至有时弊大于利。但对于“幸运”的深度学习来讲,我们经常遇到的是凸优化问题,因而梯度下降法取得了良好的结果。但对于强化学习,我们通常遇到很多非凸函数,并且由于网络很深,所以我们无法判断有多少个非凸函数。
优化问题在深度学习中的作用远不止求解最终结果这么简单,它在网络架构的设计中同样起到不容忽视的作用。例如我们熟知的残差网络,其设计的初衷即为了简化优化,换句话说即回答了为什么识别函数难以训练。Nocedal 表示探索这个问题的动机包含了如下三方面:1)计算噪声;2)深层神经网络的对抗训练;3)解决增强学习以及深度神经网络的优化问题。
那么如何解决这些情况下的优化问题呢?具体来说,假设我们希望最小化一个非线性函数,这个函数需要是光滑的(但并不需要是凸的),我们可以获得函数的估值但不知道它的梯度,同时,函数估值包含了噪声,那么,对一个有着上千个变量的这样的函数来说,是否存在一种算法能够很好的处理这类函数的优化问题?
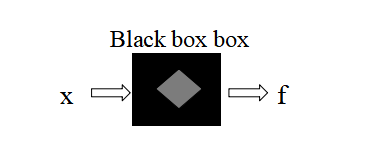
目前来说,这仍是一个十分前沿的问题,我们还不能获得“最好算法”的确切答案。但 Jorge Nocedal 教授提出了解决这一问题的一种思路。这一思路将尝试计算梯度和噪声的近似值,并通过对噪声的拟牛顿法更新建立二次模型。Nocedal给我们列举了一个黑箱的例子:假设有一个光滑的函数(x),但我们无法直接观察Φ(x)而只能观察到包括了(x)和噪声的f(x),那么我们希望在只观察f(x)的情况下最小化Φ(x)并计算出梯度近似g。
图2: 黑箱子实例
在进行噪声计算时,我们需要考虑一些不同的场景。其中一个场景是,我们需要用自适应的方法或是迭代线性求解,而另一个场景是,我们需要考虑包括舍入误差在内的随机误差。我们希望我们的方法可以适用于这些不同的场景。同时,对深度神经网络的对抗训练,我们可以观察深度神经网络的输入和输出,但不进行反向传播计算,而是对灵敏度进行分析。如下图3所示,这里假设是一个图像分类问题,那么,我们可以通过改变图像的一些部分获得完全不同的分类结果。我们主要对这些变化的部分进行分析,而不需要知道模型的导数,或是神经网络的各种公式。
图3: 灵敏度分析
二、零阶优化方法综述
所谓零阶优化方法,其本质为不计算目标函数的导数来计算目标函数的最值问题。在过去的二十年里,数学研究者已经设计了大量的无导数优化方法,最著名的包括直接搜索法和函数信赖域插值法。早期的方法包括:Nelder-Mead方法、模拟退火和遗传算法。而相比于直接搜索法而言,在噪声存在的情况下,函数信赖域插值法比其他无导数优化技术鲁棒性更强。Moré和Wild同时在其发表的文章中论述到[2],直接搜索方法速度慢,不能很好地适应问题的维数;且函数插值法在最小化噪声函数方面更有效。但Nocedal指出,这些方法都是对离散的函数起作用,对连续的函数而言这些方法并没有很好的扩展性。2010年,Moré和Wild结合多年的研究经验,在文章中[2]大胆提到:
careful study dispels many myths about such methods. They found that the best method was one learn from the function values observed and creates a model of the objective..(仔细研究消除了许多关于这些方法的神话。他们发现最好的方法是从观察到的函数值中学习并建立目标的模型。)
如下图所示:
图4: 利用多点真实值构造二次插值函数
我们不妨假设我们可以获取到原始函数的五个真实值,那么我们可以根据这五个真实值来建立二次插值函数,并在信赖域中(信赖域一般不建议设置的过大)求该函数的最小值,函数形式为:
由上式我们不难看出,如果我们想要利用纯插值方法来构建二次函数模型,并且在构建的模型中防止引入太多的噪声而导致函数非凸,那么:
至少需要(d+1)(d+2)/2个函数值,来确保我们可以获得一个完整的Hessian矩阵;
假设最小值的范数由Hessian矩阵更改,那么可以使用 O(d) 个点;
运算成本高:d∧4;
插值点倾向于位于子空间上。
Nocedal在报告中提到,虽然上述构建二次目标函数的方法运算成本较高,但是由于构建方法简单直观,因此他一度认为这种构建方法是正确的。但是,随着研究的深入,他发现该方法也有自己比较突出的问题:
①不需要特别努力来计算好的梯度估计,但我们需要特别注意整个二次模型的质量;
②信赖域估计的依赖性较强,如果信赖域较小,那么步长需要设计的较小,如果信赖域较大,那么步长需要较大,但因此在信赖域中会更容易引起震荡;
③不可并行化。
因此 Nocedal及其合作者Berahas, Byrd在2018年的文章中“Derivative-Free Optimization of Noisy Functions via Quasi-Newton Methods” 将该方法进行了改进,改进后的方法:
1) 努力逼近梯度;
2) 将模型的构造委托给拟牛顿法(BFGS);
3) 恢复哈明提出的想法。
那么噪声函数的导数是什么意思呢?Nocedal在本次讲座中为我们分享了两种方法:
方法一:高斯平滑(Gaussian Smoothing)
假设函数中带有噪声,如下图所示,我们不妨假设在x上叠加一个沿高斯方向的随机小位移δμ,那么形成的新函数和原始的函数非常近似。接着计算平滑函数的导数,
计算的公式非常像有限差分,那么我们如何精确的计算梯度呢?如下图所示,我们首先给出一个随机的初始值,接着从该初始值开始,沿着高斯方向逐步移动,用有限差分的近似值乘以我们找到的方向(当然,我们的方向也可以取高斯方向的平均值),这样就可以计算出最后的导数。这样的计算方法在一些机器学习中是非常有效的,但是对科学中的其他应用并不是很友好,所以我们还可以采用第二种方法。
方法二:带有噪声估计的有限差分法(Finite Differences with Noise Estimation)
在一些科学应用领域,有限差分法是更为经典的求解方法,当然,我们考虑的并非简单呐的差分,而是更近一步,将噪声估计包含在计算中。Moré-Wild 在2012年发表的著作中提到:
if we can estimate the noise level, we can compute a good finite-difference interval h
如果我们能估算噪声,我们将可计算出有限差分中好的步长h.
由于噪声水平通常是随机噪声的标准差,因此一旦我们可以估算出噪声∈f,那么前向差分h的表达式如下所示:
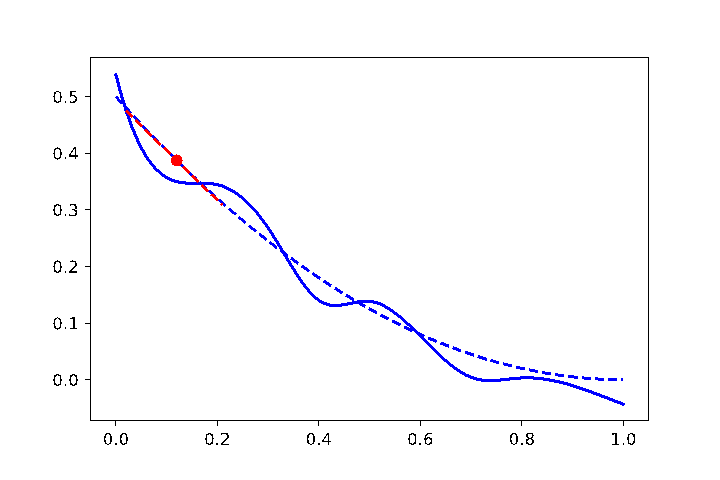
例如,如下图5所示,我们已知噪声的标准差为0.025,x = 0.12; 那么由上述前向差分h的表达式我们可以计算出h_correct = 0.28,如果选择的h更接近于正确的值,那么拟合的效果会更好,如果相差较远,那么拟合效果会大打折扣。
图5: 不同的h对最终拟合结果的影响
那么问题来了,我们该如何估算出噪声,并且估算方法既适用于随机性,又适用于确定性呢?Nocedal在本次讲座中也为我们分享了他对函数噪声估算的想法。
Noise estimation (for deterministic or stochastic noise)
为了估算函数![]() 的噪声水平,也就是
的噪声水平,也就是
在x处,选择随机的方向v,估算f在同等空间的q+1个点的值x+ibv:
然后,我们根据Hamming Difference Table,其中
搜索在计算中需要的值,
图6:Hamming Difference Table
我们发现,光滑函数的高阶差分很快趋于零,而差分在噪声中是从零开始的。我们将其看作是一个可被观察的改变标志。同时,我们看到,整个过程是尺度不变的。继续看上图所示的汉明差分表,我们看到最后一行的数值是不同的。这是由于,我们的函数中带有随机的噪声(如果没有随机噪声,那么在同一点上采样的结果应该是相同的),因此我们使用这些带有噪声的值(或平均值)带入到数值算法中,这些随机的噪声将会对结果起作用。
那么有读者会产生疑问,一旦我们由上述提及的方法获取到了相对应的梯度,那么为什么我们不使用拟牛顿模型呢?如噪声有限差分 BFGS 模型?大家的想法非常正确,但实际上目前还没有人这么做。主要原因是对噪声函数的差分是十分危险的,不好的迭代可以造成灾难性后果。
在Nocedal的算法中,我们将对每次迭代的噪声进行估算,并根据估算结果计算有限差分的步长h,在获取到对应的梯度后,我们就可以使用拟二阶牛顿法作为模型进行线性搜索,总结一下,Nocedal的整体算法流程如下:
① 在每一次迭代的过程中估算噪声;
② 根据噪声估算有限差分的步长h;
③ 由有限差分公式计算梯度;
④ 计算二次拟牛顿法的搜索方向;
⑤ 进行线性搜索;
⑥ 如果搜索值没有收敛,那么继续重复上述的步骤。
这里线搜索起到了两个作用:其一是在有限差分区间合适的情况下帮助决定步长,其二是帮助决定是否需要重新估计噪声水平。
对于零阶优化的算法验证,Nocedal及其合作者也非常有信心,在Nocedal近期发表的论文[1]中,我们看到如下图7的实验结果:在使用相同的初始值进行迭代的不同算法中,Nocedal提出的算法在迭代12步之后,会更快的收敛,达到先验的噪声水平。
图7: 算法验证实验分析结果
三、结语
Nocedal在本次讲座中为大家分享了深度学习中隐形的“核武器”---函数优化。不少做深度学习工作的读者都了解,在做许多问题中,例如:目标检测和识别、人体跟踪、语音识别、广告推荐等,设计一个好的损失函数与设计一个好的网络几乎同样重要。损失函数,实际就是我们优化中的目标函数,而如何寻找损失函数的解,其本质就是优化问题。Nocedal教授为我们讲解了噪声估计、步长的精确设置、梯度的计算以及搜索方向的计算,将优化问题庖丁解牛般拆分开来,可谓“功力十足”。同时他还提出了一些非常前沿的思想,例如:优化方法也会潜在的影响网络的结构、我们是否可以将求解偏微分方程的过程与优化方法进行结合,从而设计求解偏微分方程的深度神经网络、如何将噪声的分析应用于深度学习的灵敏度分析等等,都非常值得大家深入思考。非凸优化的求解方法中仍然存在不少难点,感兴趣的读者可进一步阅读教授及其合作者的文章,进行深入研究和探索。
关注“北京智源人工智能研究院”公众号,回复关键词“Jorge Nocedal”下载PPT。
点击“阅读原文”进入智源社区,与AI爱好者们一起参与本文讨论。
参考文献
[1] Yuchen Xie, Richard H. Byrd, and Jorge Nocedal. (2020) Analysis of the BFGS Method with Errors. SIAM Journal on Optimization 30:1, 182-209.
[2] Jorge J. Moré and Stefan M. Wild ´ , Benchmarking Derivative-free Optimization Algorithms, SIAM Journal on Optimization, 20 (2009), pp. 172–191.
[3] Jorge J. Moré and Stefan M. Wild , Estimating Computational Noise, SIAM J. Sci. Comput., 33(3), 1292–1314. (23 pages).
![]()
![]()
![]()
![]()