3.20 k近邻/数据集举例 ——读《python机器学习基础教程》第二章
样本数据集
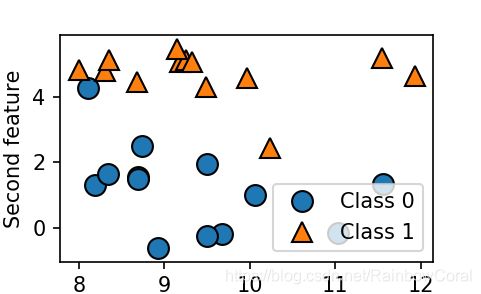
forge数据集
包含26 个数据点和2 个特征(shape函数)
#生成数据集
X, y = mglearn.datasets.make_forge()
#数据集绘图
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.legend(["Class 0", "Class 1"],loc=4)
plt.xlabel("First feature")
plt.ylabel("Second feature")
print("X.shape:{}".format(X.shape))
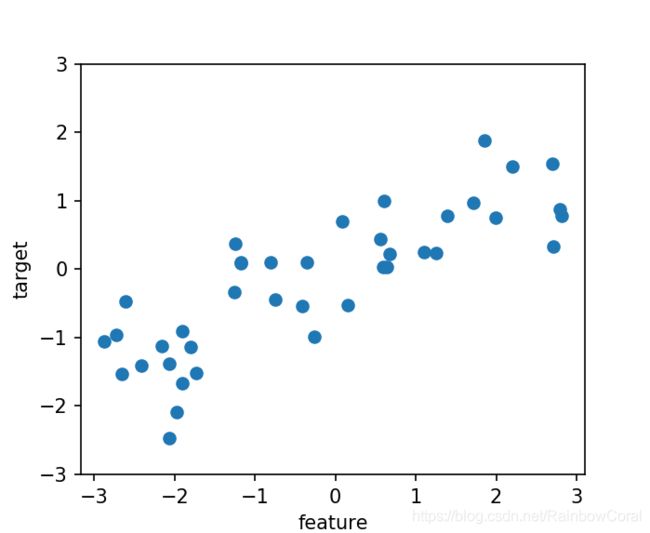
plt.show()wave数据集
X, y = mglearn.datasets.make_wave(n_samples=40)
#数据集绘图
plt.plot(X,y,'o')
plt.xlabel("feature")
plt.ylabel("target")
plt.ylim(-3,3)威斯康星州乳腺癌数据集(简称cancer)
import numpy as np
#数据集3 cancer
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print("cancer.keys():{}\n".format(cancer.keys()))
print("shape of cancer data:{}\n".format(cancer.data.shape))
print("sample counts per class:\n{}\n".format(
{n:v for n, v in zip(cancer.target_names, np.bincount(cancer.target))}))
print("feature names:\n{}\n".format(cancer.feature_names))cancer.keys():dict_keys(['data', 'target', 'target_names', 'DESCR', 'feature_names', 'filename'])
sklearn.datasets中的数据集被保存为bunch对象,可以用点操作符来访问对象的值(比如用bunch.key 来代替bunch['key'])。
shape of cancer data:(569, 30)
数据集中有569个数据点,30个特征
sample counts per class:
{'malignant': 212, 'benign': 357}# 在569 个数据点中,212 个被标记为恶性,357 个被标记为良性:波士顿房价数据集。
与这个数据集相关的任务是,利用犯罪率、是否邻近查尔斯河、公路可达性等信息,来预测20 世纪70 年代波士顿地区房屋价格的中位数
#数据集4 boston
from sklearn.datasets import load_boston
boston = load_boston()
print("data shape:{}".format(bosvvton.data.shape))包含506 个数据点和13 个特征
扩展数据集:输入特征不仅包括13个测量结果,还包括这些特征之间的乘积(也叫交互项
——包含导出特征的方法叫作特征工程(feature engineering)
#扩展数据集
X,y = mglearn.datasets.load_extended_boston()
print("X.shape:{}".format(X.shape))X.shape: (506, 104)最初的13 个特征加上这13 个特征两两组合(有放回)得到的91 个特征,一共有104 个特征
k近邻
当出现一个新的值,判断这个值最近的k个邻居,通过投票方式确定这个新值的分类标签。(一般k为奇数)
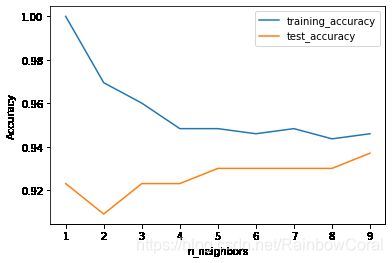
邻居越少,对应的模型更复杂,训练精度高但是测试精度低
#k近邻——分析乳腺癌数据集
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target)
training_accuracy = []
test_accuracy = []
#
neighbors_setting = range(1,10)
for n_neighbors in neighbors_setting:
#构建模型
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train,y_train)
#clf.predict(X_test)
#计算训练集和测试集精度
training_accuracy.append(clf.score(X_train,y_train))
test_accuracy.append(clf.score(X_test,y_test))
plt.plot(neighbors_setting, training_accuracy, label = "training_accuracy")
plt.plot(neighbors_setting, test_accuracy, label = "test_accuracy")
plt.xlabel("n_neighbors")
plt.ylabel("Accuracy")
plt.legend()
k近邻回归
在使用多个近邻时,预测结果为这些邻居的平均值;一个邻居时,值与最近的邻居相同
用scikit-learn 的KNeighborsRegressor实现
from sklearn.neighbors import KNeighborsRegressor
import mglearn
X,y= mglearn.datasets.make_wave(n_samples=40)
#split datasets to training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=0)
#模型实例化,邻居3
reg = KNeighborsRegressor(n_neighbors=3)
#fit model
reg.fit(X_train, y_train)
#对测试数据进行预测
print("test set prediction:{}".format(reg.predict(X_test)))
#评估泛化能力好坏
print("test set R^2:{:.2f}".format(reg.score(X_test,y_test)))
用score对回归问题的评估模型结果是R^2分数,也叫决定系数,0~1之间
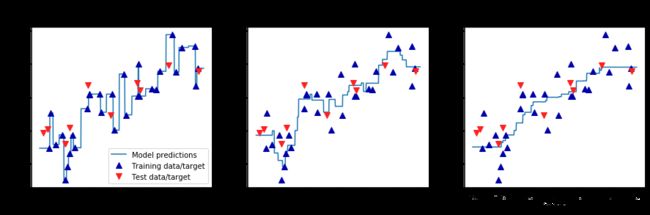
分析
# 画图分析KNeighborsRegressor
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
import mglearn
fig, axes = plt.subplots(1,3,figsize=(15,4))
#创建1000个数据点,在-3到3之间均匀分布
line = np.linspace(-3,3,1000).reshape(-1,1)
#利用1,3,9个邻居进行预测
for n_neighbors, ax in zip([1,3,9],axes):
reg = KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line,reg.predict(line))
ax.plot(X_train, y_train,'^',c=mglearn.cm2(0),markersize=8)
ax.plot(X_test, y_test,'v',c=mglearn.cm2(1),markersize=8)
ax.set_title(
"{} neighbor(s)\n train score: {:.2f} test score: {:.2f}".format(
n_neighbors, reg.score(X_train, y_train),
reg.score(X_test, y_test)))
ax.set_xlabel("Feature")
ax.set_ylabel("Target")
axes[0].legend(["Model predictions", "Training data/target",
"Test data/target"], loc="best")- 参数:KNeighbors 分类器有2 个重要参数:邻居个数与数据点之间距离的度量方法。使用较小的邻居个数(比如3 个或5 个)往往可以得到比较好的结果,但你应该调节这个参数。默认使用欧式距离
- 优点:模型简单,性能较好
- 缺点:训练集大(特征数很多或者样本数很大)可能预测速度很慢。预处理很重要。对大多数特征的大多数取值都为0 的数据集(所谓的稀疏数据集)来说,这一算法的效果尤其不好。
- 虽然k 近邻算法很容易理解,但由于预测速度慢且不能处理具有很多特征的数据集,所以在实践中往往不会用到。