3.23 线性模型 ——读《python机器学习基础教程》第二章
线性模型
1. 用于回归的线性模型
![]()
2.线性回归(普通最小二乘法OLS)
线性回归寻找参数w 和b,使得对训练集的预测值与真实的回归目标值y之间的均方误差最小。线性回归没有参数,这是一个优点,但也因此无法控制模型的复杂度。
例子:
# linear regression
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
X, y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state=42)
lr = LinearRegression().fit(X_train, y_train)
#输出w和b
print("lr.coef_:{}".format(lr.coef_))
print("lr.intercept_:{}".format(lr.intercept_))
#训练精度 测试精度
print("Training set score:{:.2f}".format(lr.score(X_train, y_train)))
print("Test set score:{:.2f}".format(lr.score(X_test, y_test)))
结果:
lr.coef_:[0.39390555]
lr.intercept_:-0.031804343026759746
Training set score:0.67
Test set score:0.66分析:可以看出训练精度 测试精度都不高,只有0.6左右,属于欠拟合,因为数据集的特征较简单而受限。
接下来分析一个高维的数据集:波士顿房价数据集(506 个样本和105个导出特征)
# linear regression_boston dataset
X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state=0)
lr = LinearRegression().fit(X_train, y_train)
# 输出w和b
# print("lr.coef_:{}".format(lr.coef_))
# print("lr.intercept_:{}".format(lr.intercept_))
# 训练精度 测试精度
print("Training set score:{:.2f}".format(lr.score(X_train, y_train)))
print("Test set score:{:.2f}".format(lr.score(X_test, y_test)))Training set score:0.95
Test set score:0.61结果显示出过拟合。
3.岭回归(L2正则化)
(可控制模型的复杂度,避免过拟合)
在岭回归中,对系数(w)的选择不仅要在训练数据上得到好的预测结果,而且还要拟合附加
约束。我们还希望系数尽量小。显示约束(L2正则化)
岭回归在linear_model.Ridge 中实现(系数都接近于0)
# ridge regression
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train,y_train)
print("Training set score:{:.2f}".format(ridge.score(X_train,y_train)))
print("Test set score:{:.2f}".format(ridge.score(X_test,y_test)))
Training set score:0.89
Test set score:0.75简单性和训练集性能二者对于模型的重要程度可以由用户通过设置alpha 参数来指定。我们用的是默认参数alpha=1.0。但没有理由认为这会给出最佳权衡。alpha 的最佳设定值取决于用到的具体数据集。增大alpha 会使得系数更加趋向于0,从而降低训练集性能,但可能会提高泛化性能
#调节alpha
from sklearn.linear_model import Ridge
ridge01 = Ridge(alpha=0.1).fit(X_train,y_train)
print("Training set score:{:.2f}".format(ridge01.score(X_train,y_train)))
print("Test set score:{:.2f}".format(ridge01.score(X_test,y_test)))
ridge10 = Ridge(alpha=10).fit(X_train,y_train)Training set score:0.93 Test set score:0.77
减小alpha 可以让系数受到的限制更小.我们预计大alpha 对应的coef_元素比小alpha 对应的coef_ 元素要小。
import matplotlib.pyplot as plt
plt.plot(ridge.coef_, 's', label="Ridge alpha=1")
plt.plot(ridge10.coef_, '^', label="Ridge alpha=10")
plt.plot(ridge01.coef_, 'v', label="Ridge alpha=0.1")
plt.plot(lr.coef_, 'o', label="LinearRegression")
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")
plt.hlines(0, 0, len(lr.coef_))
plt.ylim(-25, 25)
plt.legend()还有一种方法可以用来理解正则化的影响,就是固定alpha 值,但改变训练数据量。
4.lasso(L1正则化)
L1 正则化的结果是,使用lasso 时某些系数刚好为0。这说明某些特征被模型完全忽略。这可以看作是一种自动化的特征选
择
波士顿房价数据集用lasso
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso.coef_ != 0)))Training set score: 0.29
Test set score: 0.21
Number of features used: 4
欠拟合,结果都很差,调节alpha值,默认1
为了降低欠拟合,我们尝试减小alpha。这么做的同时,我们还需要增加max_iter 的值(运行迭代的最
大次数):
# 我们增大max_iter的值,否则模型会警告我们,说应该增大max_iter
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print("Training set score: {:.2f}".format(lasso001.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lasso001.score(X_test, y_test)))
print("Number of features used: {}".format(np.sum(lasso001.coef_ != 0)))结果Training set score: 0.90
Test set score: 0.77
Number of features used: 33
alpha 值变小,我们可以拟合一个更复杂的模型,在训练集和测试集上的表现也更好。模型性能比使用Ridge 时略好一点,而且我们只用到了105 个特征中的33 个。这样模型可能更容易理解。
但如果把alpha 设得太小, 那么就会消除正则化的效果, 并出现过拟合, 得到与LinearRegression 类似的结果
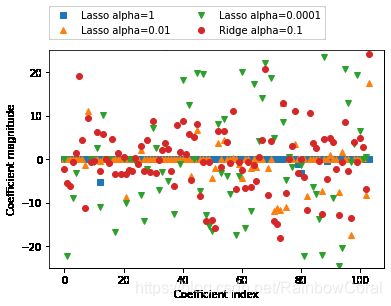
plt.plot(lasso.coef_, 's', label="Lasso alpha=1")
plt.plot(lasso001.coef_, '^', label="Lasso alpha=0.01")
plt.plot(lasso00001.coef_, 'v', label="Lasso alpha=0.0001")
plt.plot(ridge01.coef_, 'o', label="Ridge alpha=0.1")
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel("Coefficient index")
plt.ylabel("Coefficient magnitude")alpha=0.0001 时,我们得到正则化很弱的模型,大部分系数都不为0,并且还很大
在实践中,在两个模型中一般首选岭回归。但如果特征很多,你认为只有其中几个是重要的,那么选择Lasso 可能更好。同样,如果你想要一个容易解释的模型,Lasso 可以给出更容易理解的模型,因为它只选择了一部分输入特征。scikit-learn 还提供了ElasticNet类,结合了Lasso 和Ridge 的惩罚项。在实践中,这种结合的效果最好,不过代价是要调节两个参数:一个用L1正则化,一个用L2正则化。
5.用于分类的线性模型