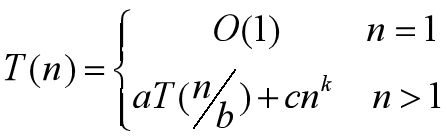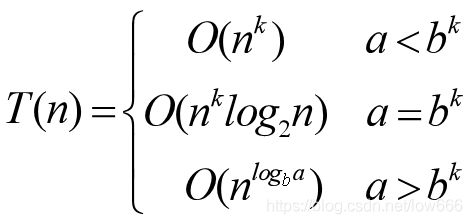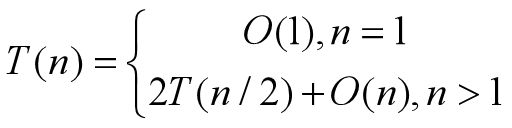算法之分治法(java)求最大最小值,归并排序,快速排序
算法之分治法(java)求最大最小值,归并排序,快速排序
1.分治法的设计思想
将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
1.1分治算法时间复杂度的递归关系式
递归算法的运行时间通常满足一个递归方程式,通过求解递归方程,就可以得到分治算法的时间复杂度。
下面给出一个定理,这个定理给出了一类递归方程的解,而大多数分治算法的运行时间满足这样一个递归方程。
1.2 分治法适应的条件
- 问题的规模缩小到一定的程度就可以容易地解决
- 问题可以分解为若干个规模较小的相同问题
- 问题分解出的子问题的解可以合并为该问题的解
- 问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题
2.案例:求最大最小值
给定一个含有几个元素的整型数组a[1:n],用分治法来求这个数组的最大元素和最小元素。
package com.sun.main;
import java.util.Scanner;
public class MaxMin {
public static void main(String[] args)
{
int array[]={-12,9,-4,6,8,11,28};
int []Max=new int[1]; //java对于实参传递,是采用值传递,所以要改成数组,不能直接使用变量去计算最大值和最小值。
int []Min=new int[1];
new MaxMin().max_min(array,0,array.length-1,Max,Min);
System.out.println("最大值: "+Max[0]);
System.out.println("最小值: "+Min[0]);
}
public static void max_min(int []a,int left,int right,int []maxnum,int []minnum)
{
if (left==right) //当只有一个元素时候,直接得出最大值和最小值
{
maxnum[0]=a[left];
minnum[0]=a[right];
}
else if (left+1==right)//当数组中有两个元素时,直接判断哪个元素大,哪个元素小
{
if (a[left]>a[right])
{
maxnum[0]=a[left];
minnum[0]=a[left];
}
else
{
maxnum[0]=a[right];
minnum[0]=a[left];
}
}
else //当数组元素的个数大于2以上的操作。
{
int m=(left+right)/2;
int lmax[]={0};
int lmin[]={0};
int rmax[]={0};
int rmin[]={0};
max_min(a,left,m,lmax,lmin);
max_min(a, m+1, right, rmax, rmin);
if(lmax[0]>rmax[0])
{
maxnum[0]=lmax[0];
}
else
{
maxnum[0]=rmax[0];
}
if(lmin[0]<rmin[0])
{
minnum[0]=lmin[0];
}
else
{
minnum[0]=rmin[0];
}
}
}
}
结果:
2.1算法分析
用T(n)来表示算法MaxMin的比较次数,n为元素个数,且为简化问题,设n为2的整数幂,即设n=2k,则T(n)满足下列关系。
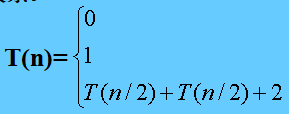
当n>2时用递推方法来求解这个递归方程可得
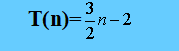
3.归并排序
3.1 基于分治策略的归并排序算法的基本思想
给定含有n个元素的整型数组a[low:high],现在要对这个数组以递增序排序,则归并排序算法的思想是:
- 若n=1,即low=high,则认为问题的规模足够小,可以直接求解;
- 若n>1,即low
3.2代码
package com.sun.main;
import java.util.Arrays;
import java.util.Scanner;
public class Merge {
public static void main(String[] args) {
// TODO Auto-generated method stub
int[] arr=new int[]{1,3,5,7,9,2,4,6,8,10};
int[] temp=new int[100];
int start=0; //java对于实参传递,是采用值传递,所以要改成数组,不能直接使用变量去计算最大值和最小值。
int mid=4;
int end=9;
int[] result=merge(arr,start,mid,end,temp);
System.out.println("结果:"+Arrays.toString(result));
}
private static int[] merge(int[] arr, int start, int mid, int end, int[] temp) {
int m = mid;
int n = end;
int i = start;
int j = mid + 1;
int z = 0;
while (i <= m && j <= n) {
if (arr[i] < arr[j]) {
temp[z++] = arr[i++];
} else {
temp[z++] = arr[j++];
}
}
while (i <= m) {
temp[z++] = arr[i++];
}
while (j <= n) {
temp[z++] = arr[j++];
}
for (i = 0; i < z; i++)
arr[start + i] = temp[i];
return arr;
}
}
结果:
分析:
4.快速排序
原理:快速排序实质是对冒泡排序的一种改进。冒泡排序基本思想是反复的比较相邻的两个元素,如果是逆序关系就交换。快速排序改进的着眼点是它并不是将两个相邻的元素进行比较,而是让相隔很远的两个数进行比较,元素交换的次数大大减少。
代码
package com.sun.main;
public class qsort {
public static void main(String[] args) {
int arr[] = new int[]{4,3,3,7,9,122344,4656};
int len = arr.length-1;
arr=qsort(arr,0,len);
for (int i:arr) { //int i:arr等价于int i ; i < arr.length() ; i++
System.out.println(i);
}
}
public static int[] qsort(int arr[],int start,int end) {
int pivot = arr[start];
int i = start;
int j = end;
while (i<j) {
while ((i<j)&&(arr[j]>pivot)) {
j--;
}
while ((i<j)&&(arr[i]<pivot)) {
i++;
}
if ((arr[i]==arr[j])&&(i<j)) {
i++;
} else {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
if (i-1>start) arr=qsort(arr,start,i-1);
if (j+1<end) arr=qsort(arr,j+1,end);
return (arr);
}
}