Concise Mercurial Vector Commitments and Independent Zero-Knowledge Sets with Short Proofs 学习笔记

1. 背景知识

1）2003年，[MRK] S. Micali，M.-O. Rabin和J. Kilian的论文《Zero-Knowledge Sets》中首次提出了zero-knowledge sets(ZKS) primitive：
允许prover commit to a secret finite set $S$ so as to be able to prove statements such as $x\in S$ or $x\notin S$ without revealing anything else on $S$, not even its size。同时指出，zero-knowledge elementary databases(ZK-EDB)可概括为：zero-knowledge sets in that each element $x$ has an associated value $D(x)$ in the committed database。Micali在该论文中构建了一个ZK-EDB based on the discrete logarithm assumption 和 use an extension of Pedersen’s trapdoor commitment[23]，有trusted setup 需构建CRS。

2）2005年，Chase等人的论文《Mercurial Commitments with Applications to Zero-Knowledge Sets》中指出，ZKS protocol可由mercurial commitment构成。[MRK]的构建是由mercurial commitments和a Merkle tree组成，Merkle tree的每个internal node 包含a mercurial commitment to its two children。
博客 水银承诺mercurial commitment 中有介绍mercurial commitment知识。

mercurial commitment是binding 属性更灵活的commitment，分为:

• hard commitment：可hard/soft-opened to only one message。可支持软打开和硬打开，且软打开的值应与硬打开的值一致。
• soft commitment：可soft-opened to any arbitrary message without committing the sender to a specific one。仅支持软打开，不支持硬打开。

hard commitment和soft commitment应是computationally indistinguishable。

3）2008年，Catalano等人[CFM]论文《Zero-Knowledge Sets with Short Proofs》中指出：
之前构建的zero-knowledge database[21,10] 都是基于a binary Merkle tree of height $O(\lambda )$，其中$\lambda$为security parameter。Each internal node contains a mercurial commitment to (a hash value of) its two children whereas each leaf node is a mercurial commitment to a database entry. A proof of membership for the entry x consists of a sequence of hard openings for commitments appearing in nodes on the path from leaf x to the root. Proofs of non-membership proceed similarly but rather use soft openings along the path. 这种方式生成的proof经常是过长的。
将binary扩展为$q$，2008年 Catalano等人[CFM]论文《Zero-Knowledge Sets with Short Proofs》 提出了trapdoor $q$-mercurial commitment（qTMC）的概念，允许一次commit to a vector of $q$ messages at once，且open时可open指定位置的message，不需要将$q$个message全部reveal。该方式构建的soft commitment openings仅需一个group element，从而大幅缩短了non-membership proof的长度；但是hard openings为$O(q)$ elements，从而membership proof的长度$O(\lambda \cdot q/\log (q))$比non-membership proof的长度要长很多。

4）本论文，2010年，Benoît Libert和Moti Yung 的论文《Concise Mercurial Vector Commitments and Independent Zero-Knowledge Sets with Short Proofs》在[CFM] qTMC的基础上，提出：

• a concise mercurial vector commitment，具有如下特性：
  （1）hard and soft position-wise openings both have constant size（independent of $q$）。
  （2）the committer can hard-open the commitment at position $i\in \{1,\cdots ,q\}$ without revealing anything on messages at other positions in the vector。
  （3）membership proof和non-membership proof的长度均较短，$O(\lambda /\log (q))$。取$q=128$，proof可不超过2KB。

• 可转化为concise multi-trapdoor qTMC scheme，以支持构建independent zero-knowledge databases，从而实现ZK-EDB的independence和short proof。

1.1 Complexity assumption

基于的假设为$q$-Diffie-Hellman Exponent (q-DHE)：已知$(g,g^{\alpha },\cdots ,g^{{\alpha }^q},g^{{\alpha }^{q+2}},\cdots ,g^{{\alpha }^{2q}})$，计算$g^{{\alpha }^{q+1}}$的难度很高。

1.2 Trapdoor $q$-Mercurial Commitment

Trapdoor $q$-Mercurial Commitment 由一系列算法组成（qKeygen, qHCom, qHOpen, qHVer, qSCom, qSOpen, qSVer, qFake, qHEquiv, qSEquiv）。

• qKeygen($\lambda ,q$)：基于security参数$\lambda$和单次commit支持的消息数$q$，输出为public/private keys $(pk,tk)$。

• qHCom${}_{pk}$($m_1,\cdots ,m_q$)：基于public key $pk$，输出hard commitment $C$ 和 辅助状态state信息$aux$。

• qHOpen${}_{pk}$($m,i,aux$)：为hard opening 算法。Given a pair $(C,aux)=$qHCom${}_{pk}$($m_q,\cdots ,m_q$)，it outputs a hard de-commitment $\pi$ of $C$ w.r.t. position $i$ if $m=m_i$. If $m\ne m_i$, it returns $\perp$.

• qHVer${}_{pk}$($m,i,C,\pi$)：为hard verification算法。若$\pi$ gives evidence that $C$ is a commitment to a sequence $(m_1,\cdots ,m_q)$ such that $m_i=i$，则输出$1$，否则输出$0$。

• qSCom${}_{pk}$()：为probabilistic 算法用于生成soft commitment和辅助信息$aux$。Such a commitment is not associated with a specific sequence of messages。

• qSOpen${}_{pk}$($m,i,flag,aux$)：生成一个soft de-commitment $\tau$ of $C$ to the message $m$ at position $i$。$flag\in \{\mathbb{H},\mathbb{S}\}$ 变量代表辅助state信息$aux$对应为hard commitment $(C,aux)=$qHCom${}_{pk}$($m_1,\cdots ,m_q$) 还是 soft commitment $(C,aux)=$qSCom${}_{pk}$()。若$flag=\mathbb{H}且m\ne m_i$，则该算法返回错误信息$\perp$。

• qSVer${}_{pk}$($m,i,C,\tau$)：returns $1$ if $\tau$ is a valid soft de-commitment of $C$ to $m$ at position $i$ and $0$ otherwise. If $\tau$ is valid and $C$ is a hard commitment, its hard opening must be to $m$ at index $i$。

• qFake${}_{pk,tk}$()：为随机算法，将trapdoor $tk$ 作为输入，输出为a $q$-fake commitment $C$ 和辅助信息$aux$。$C$不与任何消息绑定。The $q$-fake commitment $C$ is similar to a soft de-commitment with the difference that it can be hard-opened using the trapdoor $tk$。

• qHEquiv${}_{pk,tk}$($m_1,\cdots ,m_q,i,aux$)：为 non-adaptive hard equivocation algorithm. Given $(C,aux)=$qFake${}_{pk,tk}$()，生成a hard de-commitment $\pi$ for $C$ at the $i$-th position of the sequence $(m_1,\cdots ,m_q)$。 该算法为non-adaptive是因其要求the sequence of messages必须是确定的 be determined once-and-for-all before the execution of qHEquiv。

• qSEquiv${}_{pk,tk}$($m,i,aux$)：为soft equivocation algorithm。Given $(C,aux)=$qFake${}_{pk,tk}$()中的辅助信息$aux$，it creates a soft de-commitment $\tau$ to $m$ at position $i$。

Standard trapdoor mercurial commitment可认为是$q=1$的qTMC特例。



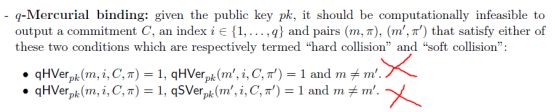
Equivocation含糊其辞：
使得adversary无法区分真实的commitment/de-commitment和基于trapdoor $tk$伪造的commitment/de-commitment。

1.3 Zero-Knowledge Sets and Databases

An elementary database $D$ (EDB) is a set of pairs $(x,y)\subset \{0,1{\}}^{\ast }\times \{0,1{\}}^{\ast }$，其中$x$为key，$y$为相应的value。
A zero-knowledge EDB要求可提供“$x\in [D]andy=D(x)$ is the associated value”或“x\notin [D]”的相应证明 without revealing any further information on $D$ (not even the cardinality of [$D$])。

Zero-knowledge sets可认为是所有value值均为$1$的ZK-EDB的特例。

EDB scheme由（CRS-Gen,P1,P2,V）算法组成：

2. Concise qTMC Scheme

本文构建的concise qTMC scheme是基于Camenisch等人2009年论文《An Accumulator Based on Bilinear Maps and Efficient Revocation for Anonymous Credentials》的accumulator累加器思路（该思路又是受Boneh等人2005年论文《Collusion Resistant Broadcast Encryption with Short Ciphertexts and Private Keys》启发）。

Camenisch等人2009年论文《An Accumulator Based on Bilinear Maps and Efficient Revocation for Anonymous Credentials》中的思路为：
public key：$(g,g_1,\cdots ,g_q,g_{q+2},\cdots ,g_{2q})$，其中$g_i=g^{{\alpha }^i}$
待累加元素：$\nu \subseteq \{1,\cdots ,q\}$
累加算法：$V={\prod }_{j\in \nu }{g}_{q+1-j}=g_1{g}_2\cdots g_q=g^{\alpha +{\alpha }^2+\cdots +{\alpha }^q}$

待证明：$i\in \nu$
Prover提供的证明可为：$W_i={\prod }_{j\in \nu \setminus i}{g}_{q+1-j+i}=V^{{\alpha }^i}/g_{q+1}$
Verifier验证：$e(g_i,V)=e(g,W_i)\cdot e(g_1,g_q)$即可。

本论文中，为hiding属性，增加了随机数$\gamma \in {\mathbb{Z}}_p$，同时为使累加的消息$m_i\in {\mathbb{Z}}_p^{\ast }$ 对位置敏感（in a position-sensitive manner） Benoît Libert做了如下改进：

• commit to $(m_1,\cdots ,m_q)$表示为$V=g^{\gamma }\cdot {\prod }_{j=1}^q{g}_{q+1-j}^{m_j}$ 【该commitment在q-DHE assumption下具有binding属性，若q-DHE assumption不成立，则adversary可produce two distinct openings of $V$ at position $i$。同时，也可将该commitment看成是trapdoor commitment，其trapdoor key为$g_{q+1}=g^{{\alpha }^{q+1}}$，拥有该trapdoor key 的人可open 该commitment为任意值。】
• 为证明$m_i$为 the $i$-th committed message，Prover提供：$W_i=g_i^{\gamma }\cdot {\prod }_{j=1,j\ne i}^q{g}_{q+1-j+i}^{m_j}$
• Verifier验证：$e(g_i,V)=e(g,W_i)\cdot e(g_1,g_q{)}^{m_i}$即可。
• 为实现mercurial commitment 具有更灵活的binding属性，若调整Verifier的验证公式为$e(g_i,V)=e(g_1,W_i)\cdot e(g_1,g_q{)}^{m_i}$则相应的binding属性将消失。基本思路为，Prover 的commitment不再只是$V$，而是$(C,V)$，其中$\theta \in {\mathbb{Z}}_p$，当$C=g^{\theta }$时，为hard commitment；当$C=g_1^{\theta }$时，为soft commitment。Verifier验证的公式为：$e(g_i,V)=e(C,W_i)\cdot e(g_1,g_q{)}^{m_i}$

详细的mercurial commitment流程如下：

以上使用的是对称pairing，若使用非对称pairing，相应的细节调整为：

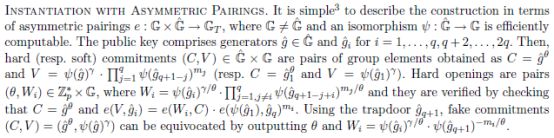
3. 基于qTMC构建ZK-EDB

2008年Catalano等人[CFM]论文《Zero-Knowledge Sets with Short Proofs》中构建ZK-EDB的思路可参见Camenisch等人2009年论文《An Accumulator Based on Bilinear Maps and Efficient Revocation for Anonymous Credentials》的附录B。
基本的思路为：对于$q$-ary tree of height $h$，将每个key $x$赋值给tree的leaf，理论上，该EBD的size 上限为$q^h$。
本论文在次基础上增加了independent zero-knowledge的要求，即 adversaries be unable to correlate their database to those created by honest provers.