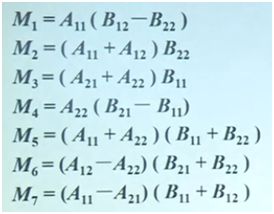分治算法中的可优化点(三)
你的打赏是我奋笔疾书的动力!
这一节来聊一聊,老生常谈的2个优化。
优化分治算法,单从降低时间复杂度的角度出发,也就是从分治算法的时间复杂度的递推公式出发,W(n)=aW(n/b)+d(n),有以下二种途径:
途径一:降低a的数值,减少子问题的个数
减少子问题数量的策略是有前提的,具体分析如下:
若这个分治算法的时间复杂度递推式满足主定理的第一个结论的条件,那么就可以得知其时间复杂度W(n)=Θ(n^logb`a),Θ是同阶符号,此时只要让对数中的a值减小,时间复杂度就会降低,a代表了划分的个数,也就是少划分几个子问题。
具体的减少策略是:找出子问题之间的依赖关系,也就是某些子问题的解可以由其他子问题依赖推导出来,那这些子问题可以减少。
例1:整数位乘问题
按上图简单划分后,A,B,C,D会被划分成4个n/2位的二进制整数,且原问题的XY乘积会由AC,AD,BC,BD,这四组乘积再数乘相加得到,这四组的乘积都是n/2位的二进制整数之间的乘积,所以,n位的二进制整数的乘积转换成了n/2位的二进制整数乘积,所以,XY2个n位二进制整数的乘积的时间复杂度为4个n/2位二进制整数的乘积的时间复杂度再加上划分以及合并子问题的解所占用的时间复杂度O(n),即:W(n)=4W(n/2)+O(n),有主定理第一结论可知,时间复杂度为:W(n)=O(n^2),和普通乘法的时间复杂度一样。
但是,经过观察和演算,发现有以下代数式:
AD+BC=(A-B)(D-C)+AC+BD,这个其实就是我们的减少子问题的策略关键,就是子问题之间有这个依赖,所以AD+BC这2个子问题可以由AC,BD,(A-B)(D-C)这3个子问题得到,所以,算法的复杂度此时为:W(n)=3W(n/2)+O(n),W(1)=1,进而由主定理第一结论可知,时间复杂度为:W(n)=O(n^log3)=O(n^1.59),比较O(n^2)好了很多。
例2:矩阵相乘问题
输入:A,B都是n阶方阵,n=2^k
输出:C=AB
普通的乘法:以元素相乘为基本运算,AB的相乘次数是n^3,所以W(n)=Θ(n^3), W(n)=O(n^3), W(n)= Ω(n^3)
简单分治算法:W(n)=O(n^3)
但是,经过观察和演算,设计M1,M2,…,M7,对应7个子问题:
矩阵的Coppersmith-Winograd算法目前最好的,上界是O(n^2.376),矩阵乘法作为一项基础的运算其应用广泛,例如:科学计算,图像处理,数据挖掘,回归、聚类、住成分分析、决策树等挖掘算法涉及大规模矩阵运算。
这个策略可能会使划分和合并子问题的工作量d(n)增加,但增加的工作量不影响W(n)的阶。
途径二:降低d(n)的阶,增加预处理
增加预处理干什么?有毛用?在分治之前,可以通过预处理一些数据来降低d(n)的阶,使得每次递归的时候d(n)不会带来一些过多的时间开销。
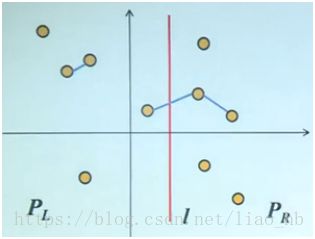
例:一个几何计算中的例子,找出一块平面点集P内的最近点对,设有n个点,n>1
普通算法:在所有点中依次不重复地选择一对点计算距离,然后比较大小,得到最小距离的一对点,时间复杂度为组合数C(n,2)=n(n-1)/2,O(n^2)
分治算法的大致思路:
- 将P划分为大小均等的2个点集PL,PR
- 分别递归计算点集PL,PR的最近点对
- 计算PL,PR各出一点组成的最近点对
- 综合2,3两种情况里的最近点对
当n=10时的一个可能样图,垂直x轴的红色垂线是一个可能的划分,如下:
算法的伪码表示:
输入:点集P,X为所有点的x坐标数组,Y为所有点的y坐标数组
输出:最近的两个点以及距离
minDistance(P,X,Y)
- 若|P|<=3,直接计算其距离
- 排序X,Y
- 用中垂线l将P分为PL,PR
- δl = minDistance(PL,XL,YL)
- δr = minDistance(PR,XR,YR)
- δ=min{δl , δr }
- 计算距离中垂线l两侧不超过δ的带状平面内的点集的最近点对,若小于δ,则以其改之。
第7步有点玄乎,有疑义,估计有改进的地方,下面来看看怎么处理比较好,先看一张图:
上图中说明了,图中的点只和绿色区域所圈的点比较,和除此之外的点比较没有意义,因为除此之外的点一定大于第6步确定的δ,那么绿色区域是怎确定的呢?宽δ是距离中线的长度,2δ是以图中点的y坐标为准,上涨δ下垂δ包括边界而来,所以在与异侧的点计算距离的时候,只选取在绿色区域内的点计算即可,若果图中Y坐标向上为正值增大方向的话,即图中的点只和异侧y坐标不超过y+δ的点进行计算,又因为每次传入的Y数组会被排序,所以一次从Y数组中确定y坐标不超过y+δ的6个连续的点来进行计算,当然排序后的X,Y数组有一个对应关系序列,为什么6个点?上图中已经说得很明白。
时间复杂度分析:
- 步1 最小子问题的求解:O(1)
- 步2 排序:O(nlgn),数量大时使用快速排序好点
- 步3 划分:O(1)
- 步4-5 分解成子问题处理:2T(n/2)
- 步6 比较:O(1)
- 步7 计算带状平面内的点集的最近点对:O(n),带状区域被中垂线一分2半,一半的点最多n/2个,而且每个点的计算距离次数是6次,则带状区域里计算最近点对的时间复杂度是O(6*n/2) = O(n)
所以综上所述的时间复杂度有:T(n)= 2T(n/2)+O(nlgn),T(2)=T(3)=O(1),因为O(1)+O(nlgn)+ O(1)+ O(1) +O(n)= O(nlgn);对以上递推式进行递归树求解有T(n)=O(n(lgn)^2),比较普通算法,有了改进,但还是没有到本讲的精华部分。
我们看到每次递归都会 对X,Y进行排序,成为了d(n)的主要“贡献”部分。我们把可以把对X,Y整体的排序放到分治之前来做一次对X,Y的排序,划分的时候,点集P一分为二PL,PR;X从中一分为二XL,XR;而Y的划分通过如下伪码:
时间复杂度分析:
和改进前的分析一样,只是步2换成了对有序数组的拆分,这个工作量是O(n),预处理的工作量是O(nlogn),所以总的时间复杂度W(n)=T(n)+O(nlogn),T(n)=2T(n/2)+O(n),T(2)=T(3)=O(1),递推式求渐进解有T(n)=O(nlogn),所以总的时间复杂度W(n)=O(nlogn)+ O(nlogn),故,W(n)= O(nlogn),比较改进前的O(n(lgn)^2)要好了很多。
具体代码见我的github
我们把结子放在这里吧,看了这么多例子,也不啰嗦了。
分治算法总结:
- 划分时要均衡
- 子问题与原问题具有相同的性质,可以用来递归
- 递归与迭代实现
- 注意递归的边界
- 通过递推方程来分析时间复杂度
- 对于满足主定理的第一个结论的条件的递推式,可以通过减少子问题的个数来优化算法
- 增加预处理,降低综合解时的开销
转载请注明出处。
参考:
https://www.bilibili.com/video/av7134874/?from=search&seid=14261249226249986779
你的打赏是我奋笔疾书的动力!
支付宝打赏:
![]()
微信打赏:
![]()