刘汝佳《算法竞赛入门经典(第二版)》习题(五)
刘汝佳《算法竞赛入门经典(第二版)》第三章习题(3-9~3-12)
习题3-9 子序列(UVa10340)
输入两个字符串s和t,判断是否可以从t中删除0个或多个字符(其他字符顺序不变)。得到字符串s。例如,abcde可以得到bce,但无法得到dc。
Input Specification
The input contains several testcases. Each is specified by two strings s, t of alphanumeric ASCII characters separated by whitespace. Input is terminated by EOF.
Output Specification
For each test case output, if s is a subsequence of t.
Sample Input
sequence subsequence
person compression
VERDI vivaVittorioEmanueleReDiItalia
caseDoesMatter CaseDoesMatter
Sample Output
Yes
Yes
解析
原题中规定时间限制2s,内存限制32MB,但没说输入字符串的长度限制,暂且按100000来做。这道题直接对s和t扫一遍即可。
#include
#include
using namespace std;
int main (void)
{
string s,t;
int i,j;
while (cin >> s >> t)
{
for (i = 0, j = 0; i < s.size() && j < t.size();)
{
if (s[i] == t[j])
{
i++;
j++;
}
else
j++;
}
(i == s.size())?cout << "yes":cout << endl;
}
return 0;
} 习题3-10 盒子(ACM/ICPC NEERC 2004,UVa1587)
给定6个矩形的长和宽wi和hi(1≤wi,hi≤1000),判断它们能否构成长方体的6个面。
Input
Input file contains several test cases. Each of them consists of six lines. Each line describes one pallet and contains two integer numbers w and h ( 1≤w, h≤10 000) -- width and height of the pallet in millimeters respectively.
Output
For each test case, print one output line. Write a single word ` POSSIBLE' to the output file if it is possible to make a box using six given pallets for its sides. Write a single word ` IMPOSSIBLE' if it is not possible to do so.
Sample Input
1345 2584
2584 683
2584 1345
683 1345
683 1345
2584 683
1234 4567
1234 4567
4567 4321
4322 4567
4321 1234
4321 1234
Sample Output
POSSIBLE
IMPOSSIBLE
解析
将6个矩形的长和宽按从小到大排列,分别判断6个矩形的长和宽能否组成长方体3组矩形(一组2个)的面,再判断这三组矩形的长和宽能否构成一个矩形。
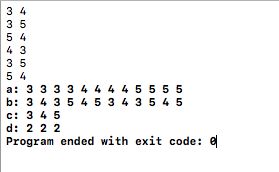
比如输入6个矩形的长和宽分别为a[(3,4),(3,5),(5,4),(4,3),(3,5),(5,4)],整理后得到a[(3,4),(3,5),(4,5),(3,4),(3,5),(4,5)],新建一个数组b存放第一次整理后的数据,对数组a全部元素按从小到大进行第二次整理得到b[3,3,3,3,4,4,4,4,5,5,5,5],再新建一个数组c存放长宽高得到c[3,4,5],用数组c与数组a比较,若与长宽高相等的边都对应有4条则从数组b中找出每组长宽都相等的矩形有几个,存放在数组d中得到d[2,2,2],若都为2则可以构成长方体。
#include
#include
using namespace std;
int main (void)
{
int a[12] = {0};
while (cin >> a[0] >> a[1])
{
int i,j;
if (a[0] > a[1])
swap(a[0], a[1]);
//输入第2~6个矩形的长宽,注意步长为2
for (i = 2; i < 12; i += 2)
{
cin >> a[i] >> a[i+1];
if (a[i] > a[i+1])
swap(a[i], a[i+1]);
}
int b[12] = {0};
memcpy(b, a, sizeof(a));
sort (a,a+12);
bool flag = true;
int c[3] = {0};
//判断与长宽高长度相等的边长是否都为4条
for (i = 0; i < 3; i++)
{
c[i] = a[i*4];
for (j = 1; j < 4; j++)
{
if (c[i] != a[i*4+j])
flag = false;
else
continue;
}
}
int d[3] = {0};
//判断三种6个矩形是否能按长宽分为3组
for (i = 0; i < 12; i += 2)
{
if (d[0] < 2 && b[i] == c[0] && b[i+1] == c[1])
d[0]++;
else if (d[1] < 2 && b[i] == c[0] && b[i+1] == c[2])
d[1]++;
else if (d[2] < 2 && b[i] == c[1] && b[i+1] == c[2])
d[2]++;
else flag = false;
}
if (!(d[0] == 2 && d[1] ==2))//有2组满足条件必定能构成长方体,当然也可以写3组
flag = false;
if (flag)
cout << "POSSIBLE" << endl;
else
cout << "IMPOSSIBLE" << endl;
}
return 0;
} 习题3-11 换低挡位置(ACM/ICPC NEERC 2006,UVa1588)
给出两个长度分别为n1,n2(n1,n2≤100)且每列高度只为1或2的长条。需要将它们放入一个高度为3的容器,问能够容纳它们的最短容器长度(附图参见刘汝佳《算法竞赛入门经典(第二版)》P59)。
Input
The input file contains several test cases, each of them as described below.There are two lines in the input, each contains a string to describe a section. The first line describes master section (teeth at the bottom) and the second line describes driven section (teeth at the top). Each character in a string represents one section unit -- 1 for a cavity and 2 for a tooth. The sections can not be flipped or rotated.Each string is non-empty and its length does not exceed 100.
Output
For each test case, write to the output a line containing a single integer number -- the minimal length of the stripe required to cut off given sections.
Sample Input
2112112112
2212112
12121212
21212121
2211221122
21212
Sample Output
10
8
15
解析
固定一个长条,用另一根长条从第一个位置开始找,找到长度契合的就开始往后验证,能完全契合视为成功,容器长度为两根长条的长度和减去重合部分长度,否则从第二个位置开始找,依此类推……成功一次之后还要反过来再找一次,因为方向不同得到的结果也不同。两次遍历的结果取最小值输出即可。与字符串查找差不多做法,只不过查找条件不同而已。
#include
#include
using namespace std;
bool test (int n, string s1, string s2)
{
for (int i = 0; i < s1.size() || i < s2.size(); i++)
if (s1[n+i]+s2[i]-2*'0' > 3)
return false;
return true;
}
int len (string s1, string s2)
{
int n = 0;
while (!test(n, s1, s2))
n++;
return max (s1.size(), s2.size()+n);
}
int main (void)
{
string s1,s2;
while (cin >> s1 >> s2)
cout << min (len (s1,s2), len (s2,s1)) << endl;
return 0;
} 习题3-12 浮点数(UVa11809)
计算机常用阶码-尾数的方法保存浮点数。如果阶码有6位,尾数有8位,可以表达的最大浮点数为0.1111111112× 2111111 。注意小数点后第一位必须为1,所以一共有9位小数(附图参见刘汝佳《算法竞赛入门经典(第二版)》P59)。
这个数换算成十进制之后就是0.998046875*263=9.205357638345294*1018。你的任务是根据这个最大浮点数,求出阶码的位数E和尾数的位数M。输入格式为AeB,表示最大浮点数为A*10B。0
Input
The input file contains around 300 line of input. Each line contains a floating-point number F that denotes the maximum value that can be represented by a certain floating-point type. The floating point number is expressed in decimal exponent format. So a number AeB actually denotes the value . A line containing 0e0 terminates input. The value of A will satisfy the constraint 0
Output
For each line of input produce one line of output. This line contains the value of M and E. You can assume that each of the inputs (except the last one) has a possible and unique solution. You can also assume that inputs will be such that the value of M and E will follow the constraints: 9 ≥ M ≥ 0 and 30 ≥ E ≥ 1. Also there is no need to assume that (M+E+2) will be a multiple of 8.
Sample Input
5.699141892149156e76
9.205357638345294e18
0e0
Sample Output
5 8
8 6
解析:
这道题关键是将十进制数转化为对应的二进制数。从阶码位数可以大概估算出数据范围是10-6。
一种解法是直接输入一个double型数据,模拟手动计算十进制转二进制的过程。对其循环除2并计数,直到小于1为止,除的次数就是阶码位数(十进制),再对计数结果循环除2转化为二进制数的位数。接下来对这个小于1的数不断乘2,将结果与1相减,若都大于10-6则计数,最后得到的计数结果就是尾数的位数。这种解法看似循环次数很多,但按最大数据1018级别,每次都减少一半,这种指数级缩减对减小数据是相当可观的。
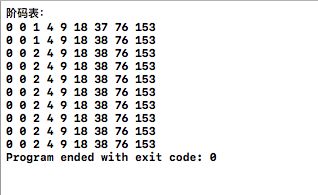
另一种解法:打表。开两个二维数组分别存放对应位数的尾数和阶码组合时尾数和指数(阶码)所能表示的最大值。因为指数是整数,所以打表完成后查表时要匹配指数来找到与其最接近的尾数。也正是因为这个原因,这道题的精度要合适,不宜过大也不宜过小。实测10-4和10-5都可以。打表完成后对应输出还需要转换格式,我的数学太渣,还是引用别人的代码吧(我真不是懒- -)。这位博主讲得很详细点击打开链接
解法一的代码如下:
#include
#include
using namespace std;
bool test (int n, string s1, string s2)
{
for (int i = 0; i < s1.size() || i < s2.size(); i++)
if (s1[n+i]+s2[i]-2*'0' > 3)
return false;
return true;
}
int len (string s1, string s2)
{
int n = 0;
while (!test(n, s1, s2))
n++;
return max (s1.size(), s2.size()+n);
}
int main (void)
{
string s1,s2;
while (cin >> s1 >> s2)
cout << min (len (s1,s2), len (s2,s1)) << endl;
return 0;
} 解法二的表格(尾数表只截了前10列):