凉肝的比赛

B.

如果局部比整体大，证明另一半是负的，所以从两头开始加和，判断正负

#include 
#include 
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 10;

ll a[MAXN], b[MAXN];
int c[MAXN];

int main(){
	int t;
	cin >> t;
	while(t--){
		ll n, judge = 0;
		cin >> n;
		memset(a, 0, sizeof(a));
		memset(b, 0, sizeof(b));
		for (int i = 1; i <= n; i++){
			cin >> c[i];
		}
		for (int i = 1; i <= n; i++){
			a[i] = a[i - 1] + c[i];
			if(a[i] <= 0)	judge = 1;
		}
		for (int i = n; i >= 1; i--){
			b[i] = b[i + 1] + c[i];
			if(b[i] <= 0)	judge = 1;
		}
		if (judge)
            cout << "NO" << endl;
        else
            cout << "YES" << endl;
	}
	return 0;
}

C.

从x的因子中寻找a,然后判断a,b的最小公倍数是不是n
LCM(a, b) == (a * b)/gcd(a,b)

#include 
#include 
using namespace std;

typedef long long ll;

ll gcd(ll a, ll b){
	return b == 0 ? a : gcd(b, a % b);
}

int main(){
	ll x;
	cin >> x;
	ll a = sqrt(x);
	for (ll i = a; i >= 1; i--){
		if (x % i == 0){
			ll b = x / i;
			ll g = gcd(i, b);
			if (i / g * b == x){
				a = i;
				break;
			}
		}
	}
	cout << a << " " << x/a << endl;
	return 0;
}

E.

数学+思维
当x = 根号下d - 1时 x + 1 + [d / x + 1]最小为2被根号下d
所以这个题只需要证明4d <= (n + 1)(n + 1)

#include 
using namespace std;

int main(){
	long long t;
	cin >> t;
	while (t--){
		long long n, d;
		cin >> n >> d;
		if (4 * d <= (n + 1) * (n + 1)){
			cout << "YES" << endl;
		}
		else{
			cout << "NO" << endl; 
		}
	}
	return 0;
} 

H.

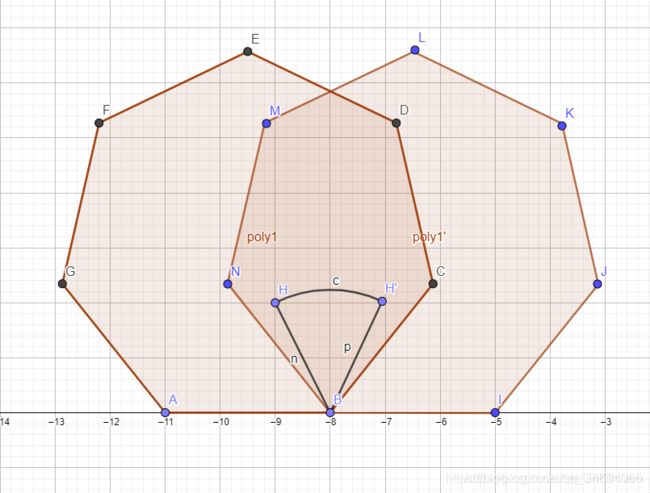
多边形内部的点的轨迹，没转一次，都是一个圆弧，c = n * ∠HBH ′
然后∠HBH ′ = π−∠NBI

#include 
#include 
#include 
using namespace std;

double x[100], y[100], xq, yq, ans;
double dis(double x, double y, double xx, double yy){
	return sqrt((x - xx) * (x - xx) + (y - yy) * (y - yy));
}

int main(){
	int t;
	int cnt = 0;
	cin >> t;
	while (t--){
		int n;
		cin >> n;
		for (int i = 0; i < n; i++)	{
			cin >> x[i] >> y[i];
		}
		x[n] = x[0]; y[n] = y[0]; x[n + 1] = x[1]; y[n + 1] = y[1];
		ans = 0;
		cin >> xq >> yq;
		for (int i = 0; i < n; i++){
			double r = dis(xq, yq, x[i + 1], y[i + 1]);
			double a1 = dis(x[i], y[i], x[i + 1], y[i + 1]);
			double a2 = dis(x[i + 1], y[i + 1], x[i + 2], y[i + 2]);
			double a3 = dis(x[i], y[i], x[i + 2], y[i + 2]);
			double cosC = (a1 * a1 + a2 * a2 - a3 * a3) / (2 * a1 * a2);
			double c = acos(-1) - acos(cosC);
			ans += (c * r);
		}
		printf ("Case #%d: %.3lf\n", ++cnt, ans);
	}
	return 0;
}