POJ - 3241 Object Clustering （曼哈顿最小生成树）

题意:

平面上有n个点集，现在把他们分成k个集合，使得每个集合中的每个点都至少有一个本集合的点之间的曼哈顿距离不大于X，求最小的X。

分析：

题目要求划分集合之后，每个集合的曼哈顿最小生成树的最长边不超过X，那么容易想到就是整个点集的曼哈顿最小生成树的第n-k条边。

求解曼哈顿距离最小生成树的方法简述：

　　如果直接两两点建边，总边数则为O(n^2)条，用时间复杂度O(N+E)的Prim算法,时间复杂度O(E*logE)的kruskal算法都是会超时的（这里N为点数，E为边数）

　　而这里的解题思路就是将边数复杂度降到O(n),因为大量的边是没有用到的，只要每45度方向距离该点最近的一个点连边即可。

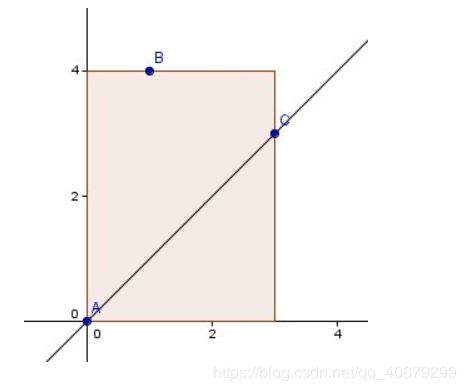
　证明就不证了，直接上结论，假如B，C都是A 在y轴向右45度区域内并且 |AB|<=|AC|,可证得|BC|<=|AC|,所以|AB|+|BC|<=|AC|+|AB|或|AC|+|BC|,即A,B,C三点距离最短为 每45度方向距离最短之和（这里距离都是曼哈顿距离） 证明博客链接：

https://blog.csdn.net/huzecong/article/details/8576908

依据上面可得只要连接每个点与八个方向距离最小的点连边即可。

　　　又因为，边是双向的，我们只要连R1,R2,R3,R4四个方向即可。比如：（上图）B是A R1最小距离点，A是B R5最小距离点，我们只要连R1,R5不连，即A连向B即可知道AB的关系。

　　思路出来了，那么怎么处理呢？我们先考虑一个方向，例如R1,(其他三个方向类比即可)。

   在某个点A(x0,y0)的这个区域内的点B(x1,y1)满足x1≥x0 且y1−x1>y0−x0。那么B就在A的R1上。

　　在A的R1区域内距离A最近的点也即满足条件的点中x+y最小的点。因此我们可以将所有点按x坐标排序，再按y−x离散。

　　用线段树或者树状数组维护大于当前点的y−x的最小的x+y对应的点（也就是维护区间最小值）这里用的是树状数组，因为代码较简单。

这样R1区域就处理完了，而其他三个区域的点只要用数学知识 翻转和对称 转化成R1处理即可。比如，R2区域将关于y=x对称(即swap(x,y))，再将关于x轴对称（即x=-x）可求R3,再关于y=x对称求R4。

//#include
#include
#include
#include
#include

#define mm(a,b) memset(a,b,sizeof(a))
#define ACCELERATE (ios::sync_with_stdio(false),cin.tie(0))
#define pii pair
#define pdd pair
#define pll pair
#define mp make_pair
#define pb push_back
#define fi first
#define se second
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
#define rush() int T;scanf("%d",&T);while(T--)
#define sc(a) scanf("%d",&a)
#define sc2(a,b) scanf("%d%d",&a,&b)
#define sc3(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define pf(a) printf("%d\n",a)
#define pf2(a,b) printf("%d %d\n",a,b)
#define pf3(a,b,c) printf("%d %d %d\n",a,b,c)
#define debug(x) cout<<#x<<": "<