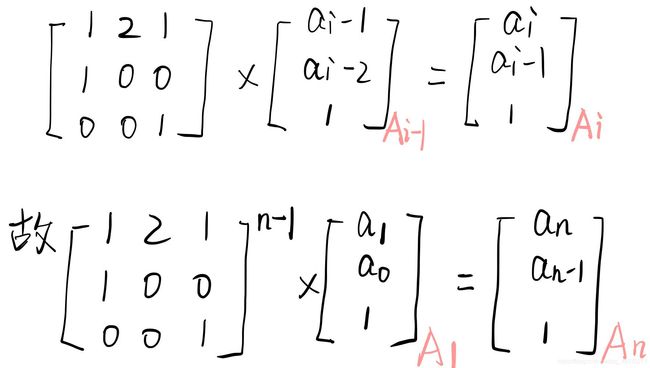矩阵快速幂

---

Learn

· 矩阵乘法

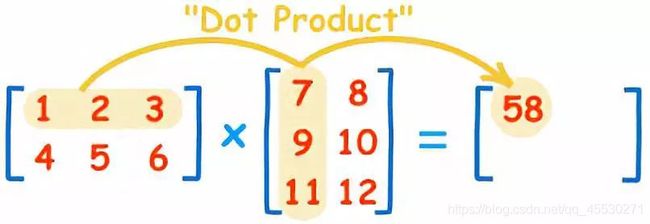
矩阵a[ i行 * k列 ] x 矩阵b[ k行 * j列 ] = 矩阵c[ i行 * j列 ]
（①第一个矩阵的列数必须等于第二个矩阵的行数，②结果矩阵的行数等于第一个矩阵的行数，列数等于第二个矩阵的列数）
c[ i ][ j ] = a[ i ][ 1 ] * b[ 1 ][ j ] + a[ i ][ 2 ] * b[ 2 ][ j ] +…+ a[ i ][ k ] * b[ k ][ j ]

· 矩阵快速幂

类比整数的快速幂，
[N * N的矩阵]¹ × [N * N的矩阵]¹ = [N * N的矩阵]²
[N * N的矩阵]² × [N * N的矩阵]¹ = [N * N的矩阵]³
所以矩阵也能快速幂，用struct封装矩阵，重载 * ^ 运算符即可实现。

struct Matrix{
	ll m[N][N];
	int size=3; //矩阵大小
	Matrix(){//根据题目进行初始化  
		memset(m,0,sizeof(m));
		m[1][1]=1;m[1][2]=2;m[1][3]=1;
		m[2][1]=1;m[2][2]=0;m[2][3]=0;
		m[3][1]=0;m[3][2]=0;m[3][3]=1;
	}
	
	void clear(){
		memset(m,0,sizeof(m));
		for(int i=1;i<=size;i++)
			m[i][i]=1;
	}
	
	void display(){
		cout<<"Matrix's begin:"<<endl;
		for(int i=1;i<=size;i++)
			for(int j=1;j<=size;j++)
				if(j<size) cout<<m[i][j]<<" ";
				else cout<<m[i][j]<<endl;
		cout<<"Matrix's end:"<<endl;
	}
	
	friend Matrix operator*(Matrix a,Matrix b){
		Matrix ans;
		for(int i=1;i<=size;i++) //size*size为矩阵大小 
			for(int j=1;j<=size;j++){
				ans.m[i][j]=0;
				for(int k=1;k<=size;k++)
					ans.m[i][j]=(ans.m[i][j]+a.m[i][k]*b.m[k][j])%mod;
			}
		return ans;
	}
	
	friend Matrix operator^(Matrix base,ll k){
		Matrix ans;
		ans.clear();
		while(k){
			if(k&1) ans=ans*base;
			base=base*base;
			k>>=1;
		}
		return ans;
	}
};

//使用方法：
//Matrix base;
//base=base^n;

---

Practice

· [HDU4990] Reading comprehension

题目链接

题意：给出1<=n,m<=1e9，序列a定义为
a[0]=0，a[i为奇数]=a[i-1]*2+1，a[i为偶数]=a[i-1]*2，计算第n项模m的结果

思路：a[0]=0，a[1]=1，a[2]=2，a[3]=5，a[4]=10，a[5]=21，a[6]=42，a[7]=85，a[8]=170
看出a(i)=a(i-1)+2*a(i-2)+1，(i>2)
所以可以如下构造矩阵，用矩阵快速幂求解

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define Inf 0x7fffffff
typedef long long ll;
const int N=100007;
ll n,mod;
int size=3;
struct Matrix{
	ll m[15][15];
	
	Matrix(){
		memset(m,0,sizeof(m));
		m[1][1]=1;m[1][2]=2;m[1][3]=1;
		m[2][1]=1;m[2][2]=0;m[2][3]=0;
		m[3][1]=0;m[3][2]=0;m[3][3]=1;
	}
	
	void clear(){
		memset(m,0,sizeof(m));
		for(int i=1;i<=size;i++)
			m[i][i]=1;
	}
	
	void display(){
		cout<<"Matrix's begin:"<<endl;
		for(int i=1;i<=size;i++)
			for(int j=1;j<=size;j++)
				if(j<size) cout<<m[i][j]<<" ";
				else cout<<m[i][j]<<endl;
		cout<<"Matrix's end:"<<endl;
	}
	
	friend Matrix operator*(Matrix a,Matrix b){
		Matrix ans;
		for(int i=1;i<=size;i++) //size*size为矩阵大小 
			for(int j=1;j<=size;j++){
				ans.m[i][j]=0;
				for(int k=1;k<=size;k++)
					ans.m[i][j]+=a.m[i][k]*b.m[k][j]%mod;
			}
		return ans;
	}
	
	friend Matrix operator^(Matrix base,ll k){
		Matrix ans;
		ans.clear();
		while(k){
			if(k&1) ans=ans*base;
			base=base*base;
			k>>=1;
		}
		return ans;
	}
};

int main(){
	while(~scanf("%lld%lld",&n,&mod)){
		Matrix base;
		base=base^(n-1);
		ll ans=0;
		ll a[4];a[1]=1;a[2]=0;a[3]=1;
		for(int i=1;i<=size;i++)		
			ans=(ans+a[i]*base.m[1][i])%mod;
		cout<<ans<<"\n";
	}
}

· [牛客寒假集训营1J题] u’s的影响力

题目链接

题意：给出1<=n,x,y,a,b<=1e12，f(1)=x，f(2)=y，f(i) = f(i-1) * f(i-2) * a^b
计算 f(n)%1000000007的值

思路：

需要注意的一点是，矩阵里的数最终都是要作为指数，因为模数mod是质数，所以对作为指数的数要%(mod-1)，最后算快速幂时再quick_pow(x,e+mod-1) [欧拉降幂]

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define Inf 0x7fffffff
typedef long long ll;
const ll mod=1000000007;
int size=3;
ll n,x,y,a,b,arr[4];
struct Matrix{
    ll m[15][15];
     
    Matrix(){//根据题目进行初始化 
        memset(m,0,sizeof(m));
        m[1][1]=1;m[1][2]=1;m[1][3]=1;
        m[2][1]=1;m[2][2]=0;m[2][3]=0;
        m[3][1]=0;m[3][2]=0;m[3][3]=1;
    }
     
    void clear(){
        memset(m,0,sizeof(m));
        for(int i=1;i<=size;i++)
            m[i][i]=1;
    }
     
    void display(){
        cout<<"Matrix's begin:"<<endl;
        for(int i=1;i<=size;i++)
            for(int j=1;j<=size;j++)
                if(j<size) cout<<m[i][j]<<" ";
                else cout<<m[i][j]<<endl;
        cout<<"Matrix's end:"<<endl;
    }
     
    friend Matrix operator*(Matrix a,Matrix b){
        Matrix ans;
        for(int i=1;i<=size;i++) //size*size为矩阵大小
            for(int j=1;j<=size;j++){
                ans.m[i][j]=0;
                for(int k=1;k<=size;k++)
                    ans.m[i][j]=(ans.m[i][j]+a.m[i][k]*b.m[k][j])%(mod-1);
            }
        return ans;
    }
     
    friend Matrix operator^(Matrix base,ll k){
        Matrix ans;
        ans.clear();
        while(k){
            if(k&1) ans=ans*base;
            base=base*base;
            k>>=1;
        }
        return ans;
    }
};
ll qpow(ll x,ll e){
    ll re=1;
    while(e){
        if(e&1){
            re=re*x%mod;
        }
        x=x*x%mod;
        e>>=1;
    }
    return re%mod;
}
 
int main(){
    cin>>n>>x>>y>>a>>b;
    x%=mod;y%=mod;a%=mod;b=b%(mod-1);
    if(n==1){
        cout<<x;
        return 0;
    }
    if(n==2){
        cout<<y;
        return 0;
    }
    Matrix base;
    base=base^(n-2);
    ll ans=1;
    ans=(ans*qpow(y,base.m[1][1]+mod-1))%mod;
    ans=(ans*qpow(x,base.m[1][2]+mod-1))%mod;
    ll t=qpow(a,b+mod-1);
    ans=(ans*qpow(t,base.m[1][3]+mod-1))%mod;
    cout<<ans%mod;
}

· [Poj3613] Cow Relays

题目链接

题意：给出一个k (<=2*t)个点，t (<=100)条边的无向连通图，求s点到e点经过n (<=1e6)条边的最短距离

思路：
思考一下，如果一个矩阵，表示走k条边后，一张图的点与点的最短路径，(a,b)表示从a到b的最短路径，然后我们把它与自己，按照矩阵乘法的格式“相乘”，把其中的乘改为取min，ans.m[i][j] = min(ans.m[i][j],a.m[i][k]+b.m[k][j])【类似于Floyd】。这样得到的是走k+k条边的矩阵，同理，一个走了a条边的矩阵×一个走了b条边的矩阵，得到的是走了a+b条边的矩阵。
所以对点离散化，用矩阵快速幂的方法，修改一下opereator重载的 * 式子求baseⁿ即可。

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=207;
int m,s,t,l[N],r[N];
ll w[N],n,Inf;
int U[N],cntu,size;
struct Matrix{
	ll m[N][N];
	
	Matrix(){//根据题目进行初始化  
		memset(m,63,sizeof(m));
	}
	
	void clear(){
		memset(m,0,sizeof(m));
		for(int i=1;i<=size;i++)
			m[i][i]=1;
	}
	
	void display(){
		cout<<"Matrix's begin:"<<endl;
		for(int i=1;i<=size;i++)
			for(int j=1;j<=size;j++)
				if(j<size) cout<<m[i][j]<<" ";
				else cout<<m[i][j]<<endl;
		cout<<"Matrix's end:"<<endl;
	}
	
	friend Matrix operator*(Matrix a,Matrix b){
		Matrix ans;
		for(int i=1;i<=size;i++) //size*size为矩阵大小 
			for(int j=1;j<=size;j++)
				for(int k=1;k<=size;k++){
					if(ans.m[i][j]==Inf)ans.m[i][j]=a.m[i][k]+b.m[k][j];
					else ans.m[i][j]=min(ans.m[i][j],a.m[i][k]+b.m[k][j]);
				}
		return ans;
	}
	
	friend Matrix operator^(Matrix base,ll k){
		k--;
		Matrix ans=base;
		while(k){
			if(k&1) ans=ans*base;
			base=base*base;
			k>>=1;
		}
		return ans;
	}
};


int main(){
    cin>>n>>m>>s>>t;
    for(int i=1;i<=m;i++){
		scanf("%lld%d%d",&w[i],&l[i],&r[i]);
		U[++cntu]=l[i];
		U[++cntu]=r[i];
	}
    sort(U+1,U+1+cntu);
    size=cntu=unique(U+1,U+1+cntu)-U-1;
    Matrix base;
	Inf=base.m[0][0];
	for(int i=1;i<=m;i++){
    	l[i]=lower_bound(U+1,U+1+cntu,l[i])-U;
    	r[i]=lower_bound(U+1,U+1+cntu,r[i])-U;
   		base.m[l[i]][r[i]]=base.m[r[i]][l[i]]=w[i];
    }
    s=lower_bound(U+1,U+1+cntu,s)-U;
    t=lower_bound(U+1,U+1+cntu,t)-U;
    base=base^n;
    cout<<base.m[s][t];
}