斯坦福大学NLP课程CS224N课第一次作业第二部分（上）

斯坦福大学NLP课程CS224N课第一次作业第二部分

第二部分包括三个python文件，同时也相当于实现三个小功能，分别是梯度检验、sigmoid和简单的神经网络。

1.梯度检验

梯度校验就是使用函数某点与其相邻点组成的直线的斜率估计该点的导数，如果相邻点为无穷小相邻，那么结果就等于该点的导数，公式解释为：
$$f^{{}^{\prime }}(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x-h)))}{2\ast h}公式一$$
下面我们看一下给我们的q2_gradcheck.py中需要我们补充的函数：

def gradcheck_naive(f, x):
    """ Gradient check for a function f.

    Arguments:
    f -- a function that takes a single argument and outputs the
         cost and its gradients
    x -- the point (numpy array) to check the gradient at
    """

    rndstate = random.getstate()
    random.setstate(rndstate)
    fx, grad = f(x) # Evaluate function value at original point
    h = 1e-4        # Do not change this!

    # Iterate over all indexes ix in x to check the gradient.
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        ix = it.multi_index

        # Try modifying x[ix] with h defined above to compute numerical
        # gradients (numgrad).

        # Use the centered difference of the gradient.
        # It has smaller asymptotic error than forward / backward difference
        # methods. If you are curious, check out here:
        # https://math.stackexchange.com/questions/2326181/when-to-use-forward-or-central-difference-approximations

        # Make sure you call random.setstate(rndstate)
        # before calling f(x) each time. This will make it possible
        # to test cost functions with built in randomness later.

        ### YOUR CODE HERE:
        raise NotImplementedError
        ### END YOUR CODE

        # Compare gradients
        reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix]))
        if reldiff > 1e-5:
            print "Gradient check failed."
            print "First gradient error found at index %s" % str(ix)
            print "Your gradient: %f \t Numerical gradient: %f" % (
                grad[ix], numgrad)
            return

        it.iternext() # Step to next dimension

    print "Gradient check passed!"

我们先看函数的输入和输出，然后判断这个函数在干嘛。输入也就是函数的参数，传入一个函数f和一个变量x，很容易判断f是关于x的函数，然后输出没有return，而是判断梯度校验是否成功。
我们逐句进行分析吧：
首先映入眼帘的是一些英文注释，它告诉我们函数参数的意义，然后前两句代码是：

rndstate = random.getstate()
random.setstate(rndstate)

这句话的意义如果不会也基本能猜到就是设置种子，首先用getstate的方法得到一个种子，然后使用setstate的方法set一个种子，那么这么做有什么意义呢。因为我们在做函数f运算的时候可能存在随机操作，但是我们在梯度校验，所以需要两次求f的随机设置是一样的，所以需要设置种子。举个例子，在第三部分要实现的word2vec模型中，我们需要进行负采样来得到错误样本，这一步就是随机操作，如果不设置种子，梯度校验就会出错。
之后的两句很简单我们一步带过，第三句就是求函数f，返回函数值和你的梯度，然后第四句是设置h的值，前面我们说h越小可能求的导数的准确性越高，但是如果太小，可能会超过python数据类型的表示范围。
第五句话就比较有意思了，其实就是生成一个生成器，不断返回x中某单个元素的值，因为x可能是个矩阵，而对于矩阵进行梯度校验的时候每次只能改变一个值，所以这个函数不断返回的就是矩阵(0,0)、(0,1)、···、（1,0）···的这些单个元素，然后进行循环，判断时候每个地方的梯度校验都正确。
然后下面就是循环了，循环判断语句就是是否生成器迭代完成，如果迭代完成就停止，下一句话ix = it.multi_index也就是每次取矩阵的一个元素的意思。
中间我们需要补充的代码我们先不管，我们直接看后面的：

reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix]))
if reldiff > 1e-5:
    print "Gradient check failed."
    print "First gradient error found at index %s" % str(ix)
    print "Your gradient: %f \t Numerical gradient: %f" % (
        grad[ix], numgrad)
    return

it.iternext() # Step to next dimension

我觉得比较明显的就可以看到grad[ix]就是你计算的梯度在ix位置的值，而numgrad是根据公式一计算得到的梯度，然后计算他们的相对差值（差值除以他们的最大值），最后判断这个相对差值是否足够小，如果不足够小就会出现梯度校验失败的输出。然后如果校验成功，就判断矩阵的下一个元素，如果矩阵中所有元素都校验成功，那么就返回梯度校验成功。
ok，现在我们已经分析完了他给的代码，而我们需要就算的就是numgrad这个参数，也就是根据公式一进行计算，我们想想如果将其转化成代码：

1. 设置种子，这是首先要做的，你如果不会就可以百度一下刚才那两个设置种子的函数，因为种子已经得到了，我们不用再次回去了，直接使用random.setstate(rndstate)即可。
2. 我们看公式的分子，我们需要计算f(x+h)和f(x-h)，这样很简单，直接上手就写：

x[ix]+=h
f_positive = f(x)[0]    #返回函数值和梯度，我们只需要函数值即可
x[ix]-=2*h
f_negative = f(x)[0]
numgard = (f_positive-f_negative)/(2*h)
numgrad = np.sum(numgrad)  #可能返回函数值是一个向量或者矩阵，直接求sum

这样我们就补充完了这个函数。

2. sigmoid

我们第二个需要实现的就是sigmoid函数及其求导，这个我们只简单说一下，因为确实比较简单。

1. sigmoid
   首先什么是sigmoid，sigmoid其实是和softmax有类似功能，不同的是sigmoid是将某个值转化为一个0-1之间的概率值，值越大那么转化之后的概率值也越大，通常用于二分类，而softmax通常用于多分类问题，下面我们看一下sigmoid公式：
   $$sigmoid(x)=\frac{1}{1+e^{-x}}公式二$$
   公式很简单，我们看看sigmoid的图是什么样的：
   
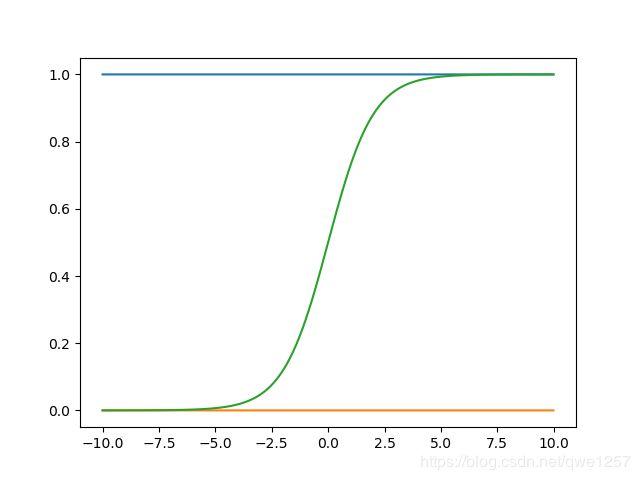
   其中绿色线是sigmoid函数，这个图是什么画的呢，其实很简单，使用的是python的matplotlib.pyplot，这个不能直接将函数传进去，而去传进去很多点然后它自动拟合曲线，所以我们要做的就是先生成函数的点，然后传进去，plot就会自动帮我们拟合，我们可以看一下画图的代码：

import numpy as np
import matplotlib.pyplot as plt
x1= np.arange(-10,10,0.01)
y1 = np.ones(x1.shape)
y2 = np.zeros(x1.shape)
y3 = 1/(1+np.exp(-x1))
y4 = np.arange(0,1,0.01)
plt.plot(x1,y1)
plt.plot(x1,y2)
plt.plot(x1,y3)
plt.show()

上面给你的代码相当于画了三天曲线，当然matplotlib还有很多用法，其他用法可以自己探索，这里我用到什么就贴什么。
回到正题，我们应该如何求使用python求sigmoid及其导数呢，首先是sigmoid函数：

def simgoid(x):
	s = 1/(1+np.exp(-x))
	return s

就是这么简单，而且也没什么好说的，直接按照公式二求即可。
接下来是sigmoid求导公式，这个我还是推导一下：
使用分数的求导公式求得：
$$sigmoid(x)=\frac{0\ast (1+e^{-x})-1\ast (-e^{-x})}{(1+e^{-x}{)}^2}\to sigmoi{d}^{{}^{\prime }}(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}$$
$$sigmoi{d}^{{}^{\prime }}(x)=\frac{e^{-x}}{(1+e^{-x}{)}^2}=\frac{1}{(1+e^{-x})}\ast \frac{e^{-x}}{(1+e^{-x})}=\frac{1}{(1+e^{-x})}\ast (1-\frac{e^{-x}}{(1+e^{-x})})$$
所以：
$$sigmoi{d}^{{}^{\prime }}(x)=sigmoid(x)\ast (1-sigmoid(x))$$
于是sigmoid导数的函数为：

def sigmoid_grad(s):
	ds = s*(1-s)
	return ds

所以公式推导之后就是这么简单。
所以的准备工作已经完成，我们下回看看怎么写一个小的神经网络，包括前向算法和BP算法。
欢迎评论交流，也欢迎关注，会将CS224N的所有作业写成博客的。