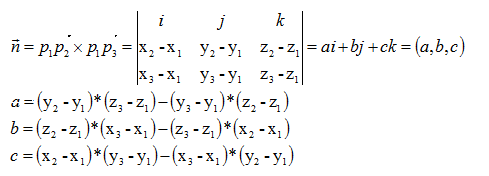已知三点求平面的法向量 —— 两种方法
最近学图形学时遇到了这个问题,PPT 给的大概是一个通过线性代数的方法求的,有点看不懂。加上线性代数早就忘光了,更加是一脸茫然。但是这个知识点在高中讲过,自己却怎么也记不起来了,直到今天突然记起来了,特此记录一下。
问题描述
已知三维空间中三点 P 1 ( x 1 , y 1 , y 1 ) , P 2 ( x 2 , y 2 , y 2 ) , P 3 ( x 3 , y 3 , y 3 ) P_1(x_1, y_1, y_1),P_2(x_2, y_2, y_2),P_3(x_3, y_3, y_3) P1(x1,y1,y1),P2(x2,y2,y2),P3(x3,y3,y3)。要求求出这三个点构成平面的法向量。
高中知识
我们不妨设平面法向量 n → = ( x , y , z ) \overrightarrow{n}=(x, y, z) n=(x,y,z)。
我们知道法向量是和平面垂直的,因此法向量也和该平面上任意一条向量相互垂直,即点积为 0。
利用这个性质,我们可以构造两个方程,此时
n → ・ P 1 P 2 → = 0 n → ・ P 1 P 3 → = 0 \overrightarrow{n}・ \overrightarrow{P_1P_2} =0\\ \overrightarrow{n}・ \overrightarrow{P_1P_3} = 0 n・P1P2=0n・P1P3=0
将 P 1 P 2 P 3 P_1P_2P_3 P1P2P3 三点坐标代入即可。
x ( x 1 − x 2 ) + y ( y 1 − y 2 ) + z ( z 1 − z 2 ) = 0 x ( x 1 − x 3 ) + y ( y 1 − y 3 ) + z ( z 1 − z 3 ) = 0 x(x_1-x_2)+y(y_1-y_2)+z(z_1-z_2) = 0 \\ x(x_1-x_3)+y(y_1-y_3)+z(z_1-z_3) = 0 x(x1−x2)+y(y1−y2)+z(z1−z2)=0x(x1−x3)+y(y1−y3)+z(z1−z3)=0
然后我们不妨假设 x=1, 这样即可求出 y z(三个方程三个未知量)。
p.s 这样求出的法向量可能会有分数,可以自行改造一下。
大学知识
在高等数学「向量代数与空间解析几何」这一章中,介绍了向量叉积的概念。其中叉积的几何表示如下:
a×b 是一种向量
方向: a×b 同时垂直于 a 和 b 且符合右手定则
我们注意到 a×b 同时垂直与 a 与 b,而这和法向量的性质刚好一致。因此我们就可以利用 P 1 P 2 → \overrightarrow{P_1P_2} P1P2 与 P 1 P 3 → \overrightarrow{P_1P_3} P1P3 的叉积来构造平面法向量。因此我们不妨假设
n → = P 1 P 2 → × P 1 P 3 → \overrightarrow{n} = \overrightarrow{P_1P_2} × \overrightarrow{P_1P_3} n=P1P2×P1P3
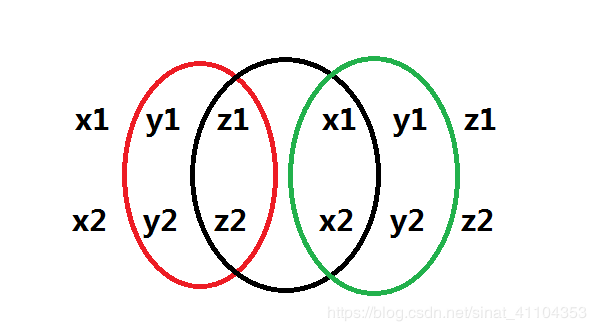
n → = ( a , b , c ) \overrightarrow{n}=(a, b, c) n=(a,b,c) 有一个更简单的记法
我们不妨设 P 1 P 2 → = ( x 1 , y 1 , z 1 ) \overrightarrow{P_1P_2} = (x1, y1, z1) P1P2=(x1,y1,z1)、 P 1 P 3 → = ( x 2 , y 2 , z 2 ) \overrightarrow{P_1P_3} = (x2, y2, z2) P1P3=(x2,y2,z2),a、b、c 三者的值对应这下面三个椭圆的行列式。即
a = y 1 z 2 − y 2 z 1 b = z 1 x 2 − z 2 x 1 c = x 1 y 2 − x 2 y 1 a = y1z2 - y2z1 \\ b = z1x2 - z2x1 \\ c = x1y2 - x2y1 a=y1z2−y2z1b=z1x2−z2x1c=x1y2−x2y1