基于PyTorch的深度学习快速入门教程

最近小组汇报正好用到了pytorch，所以想把相关内容整理成博客（汇报ppt和演示代码附在最后了，有需要的话可以自取）。主要参考了《Python深度学习：基于PyTorch》的前几章和网上的一些入门教程，侧重代码。通过这篇博客 ，你可以：

1. 对PyTorch框架有初步的了解

2. 对PyTorch中的Tensor张量、autograd自动求导、反向传播等概念有一定了解并掌握相关代码

3. 用PyTorch实现一个简单的机器学习算法（函数拟合）

4. 使用PyTorch神经网络工具箱搭建一个简单的卷积神经网络模型（minist手写数字识别）

5. 训练搭建的网络并通过该模型来进行预测
   …

---

一、PyTorch简介

1.1 PyTorch简介

PyTorch源于深度学习框架Torch，Torch使用了一种不是很大众的语言Lua作为接口，用的人不是很多，所以开发团队在Torch的基础上使用Python重写的一个全新的深度学习框架，也就是PyTorch。
虽然PyTorch的前身是Torch，但其与Torch 的不同之处在于PyTorch 不仅更加灵活，支持动态图，而且提供了Python接口。PyTorch 既可以看做加入了GPU 支持的numpy，同时也可以看成一个拥有自动求导功能的强大的深度神经网络。它更像NumPy的替代产物，不仅继承了NumPy的众多优点，还支持GPU计算，在计算效率上要比NumPy有更明显的优势；不仅如此，PyTorch还有许多高级功能，比如拥有丰富的API，可以快速完成深度神经网络模型的搭建和训练。所以PyTorch一经发布，便受到了众多开发人员和科研人员的追捧和喜爱，成为 AI从业者的重要工具之一。

1.2 PyTorch优点

• 简洁
  PyTorch追求最少的封装，尽量避免重复造轮子，不像TensorFlow中充斥着session、graph、operation、name_scope、variable、tensor、layer等全新的概念
  PyTorch的设计遵循代表高维数组（ tensor ）、自动求导（ variable\autograd）和神经网络（ nn.Module ）三个由低到高的抽象层次，而且这三个抽象之间联系紧密，可以同时进行修改和操作，其中nn.Module则是PyTorch中对所有模型对象的封装
• 易用
  现在的深度学习平台在定义模型的时候主要用两种方式：static computation graph(静态图模型) 和 dynamic computation graph(动态图模型)。 绝大部分平台都采用的是static的定义方式，包括TensorFlow, Theano, Caffe，Keras等
  静态图需要在处理数据前定义好一套完整的模型；而动态图模型允许用户先定义好一套基本的框架再根据数据来实时修正模型
  静态图定义的缺陷是在处理数据前必须定义好完整的一套模型，能够处理所有的边际情况，比如在声明模型前必须知道整个数据中句子的最大长度。相反动态图模型(现有的平台比如PyTorch, Chainer, Dynet)能够非常自由的定义模型
  PyTorch不仅定义网络结构简单，而且还很直观灵活。它支持autograd，所以不用自己去定义和数学推导back-propagation，还支持动态图模型，可以无缝衔接numpy
• 速度快
  PyTorch的灵活性不以速度为代价，在许多评测中，PyTorch的速度表现胜过TensorFlow和Keras等框架 。同样的算法，使用PyTorch实现的更有可能快过用其他框架实现的
• 社区活跃
  PyTorch提供了完整的文档，有facebook的FAIR强力支持（FAIR是全球TOP3的AI研究机构），开源方案也很多

1.3 PyTorch的安装

主要流程：

1. 在anaconda中创建python环境,并将路径添加到系统环境变量中
2. 在pytorch官网复制安装命令https://pytorch.org/get-started/locally/
3. 在命令行中安装pytorch
4. Import torch测试安装是否成功

具体可以参考博客https://blog.csdn.net/qq_38704904/article/details/95192856

二、PyTorch基础

2.1 Numpy

NumPy是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库，在机器学习和深度学习中经常用到。

2.1.1 numpy数组的定义

• 直接定义

import numpy as np
x1 = np.array([1.0, 2.0, 3.0])
X2=np.array((1.0, 2.0, 3.0))

• 将列表list转换为numpy数组

b=[2.0,4.0,6.0]
y=np.array(a)

• 将numpy数组转换为列表list

z= np.array([1.0, 2.0, 3.0]) 
c=list(z)

2.1.2 numpy数组的元素访问

对于矩阵A=np.array([1,2,3],[4,5,6])

• A[i]获得矩阵A的第i行
• A[i][j]获得元素Aij
• A[i][j:k]获得数组A[i]的j到k-1元素

2.1.3 numpy数组的计算

• 加法：x+y
• 乘法：x*y
• 广播：x*10=[1.0, 2.0, 3.0]10=[1.0, 2.0, 3.0] [10, 10, 10]

2.2 Tensors张量

2.2.1 Tensors

2.2.2 Tensors的使用

1. 导入包

import torch

2. 构建一个5*3的矩阵

x = torch.Tensor(5, 3)  # 未初始化
y = torch.rand(5, 3)  # 随机初始化

3. 将torch的Tensor转换为numpy的array

a=x.numpy() # Tensor转array
x=torch.from_numpy(a)  # array转Tensor

4. 运算：

• 加减法：y.add_(x)、z=x+y、torch.add(x,y,out=z)、z=torch.sub(x,y)
• 乘法： x*y、torch.mul(x,y)
• 裁剪：y=torch.clamp(x,-0.1,0.1)
  更多运算可参考官方说明文档

5. CUDA Tensors：
   使用 .cuda 函数将Tensors移动到GPU

if torch.cuda.is_available():
    x = x.cuda()
    y = y.cuda()

2.3 autograd自动求导

2.3.1 Variable变量
将Tensor转换为Variable之后，可以装载梯度信息，一旦前向计算,可以通过.backward()方法来自动计算所有的梯度

2.3.2 gradient descent梯度下降
损失函数关于模型参数的梯度指向一个可以降低损失函数值的方向，可以不断地沿着梯度的方向更新模型从而最小化损失函数

2.3.3 Autograd自动求导
对于复杂的模型，例如多达数十层的神经网络，手动计算梯度非常困难，因此PyTorch提供了Autograd包来自动化求导过程，它会有一个记录我们所有执行操作的记录器，之后再回放记录来计算梯度
这一技术在构建神经网络时尤其有效，因为我们可以通过计算前路参数的微分来节省时间

2.4 利用Numpy实现函数拟合

import numpy as np
from matplotlib import pyplot as plt
# 生成 输入数据x 及 目标数据y
np.random.seed(100)
x = np.linspace(-1,1,100).reshape(100,1)
y = 3*np.power(x,2)+2+0.2*np.random.rand(x.size).reshape(100,1)
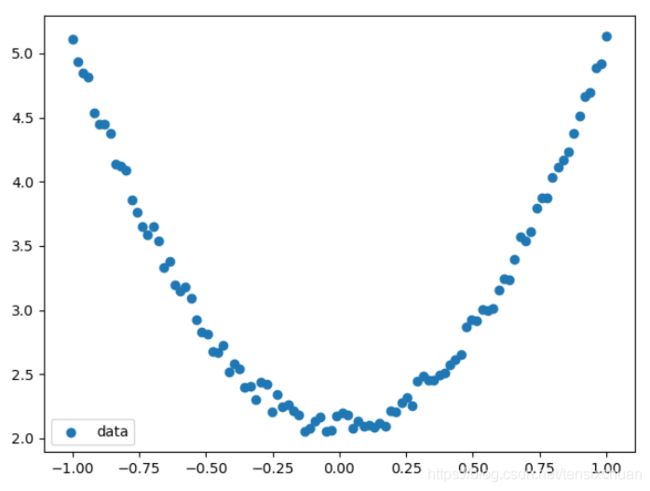
# 查看x、y数据分布情况
plt.scatter(x,y)
plt.show()
# 初始化权重参数
w1 = np.random.rand(1,1)
b1 = np.random.rand(1,1)
# 训练模型
lr = 0.001 # 学习率
for i in range(800): #梯度下降
    y_pred = np.power(x,2)*w1+b1

    loss = 0.5*(y_pred - y)**2  # 损失函数
    loss = loss.sum()  # 方差
    # 梯度下降法
    grad_w = np.sum((y_pred - y)*np.power(x,2))
    grad_b = np.sum((y_pred - y))
    w1 -= lr*grad_w  # 将学习率看作步长
    b1 -= lr*grad_b
# 可视化结果
plt.plot(x,y_pred,'r-',label='predict')
plt.scatter(x,y,color='blue',marker='o',label='true') # true data
plt.xlim(-1,1)
plt.ylim(2,6)
plt.legend()
plt.show()
print(w1,b1)

目标函数设为y_pred=w1 * x^2+b1，求解目标函数相当于求解参数w1和b1
这里定义的loss函数为0.5*(y_pred - y)^2之和，相当于方差（按照吴恩达视频，乘以0.5可以方便求导时把次方2系数消掉，所以实际乘以了0.5），loss函数值越小，误差也就越小，所以相当于求解使得loss值最小的w1和b1，这样的目标函数和实际函数是最接近的。
grad_w是w1的梯度，相当于loss对w1的偏导，grad_b是b1的梯度，相当于loss对b1的偏导，沿着梯度方向可以最快到达loss最低点。
注意，这里的梯度是我们自己手动计算得到的，大概这么个过程：

因此

    grad_w = np.sum((y_pred - y)*np.power(x,2))
    grad_b = np.sum((y_pred - y))

然后让w1和b1每次沿着梯度方向挪动一小步，这样w1和w2的梯度会越来越小，当接近0的时候也就得到了loss可能的极小值点

    w1 -= lr*grad_w  # 将学习率看作步长
    b1 -= lr*grad_b

将计算过程循环800次，输出不断更新后的w1和b1，并输出拟合图像
运行结果：



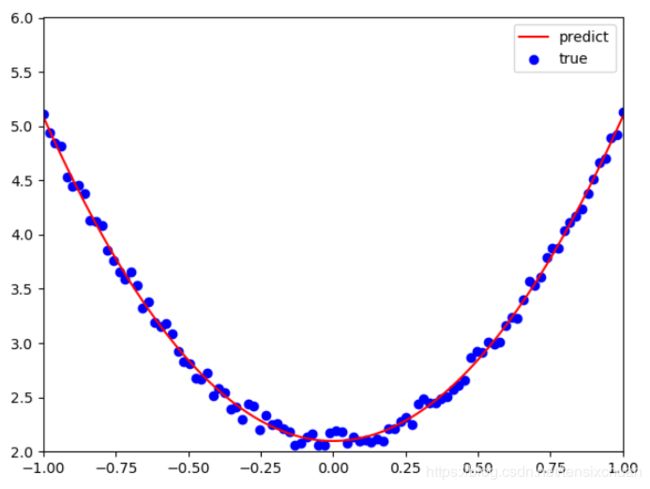
可以得出w1=2.98927619，b1=2.09818307，目标函数y_pred=2.98927619x^2+2.09818307。

2.5 利用PyTorch实现函数拟合

我们可以看到，当函数比较简单时，梯度用手动计算也很方便，但是当函数比较复杂时，计算便会十分艰巨，而pythorch的自动求导就完美解决了这一问题，只需给出正向计算过程，pytorch会自动为你反向计算梯度，接下来还是以上一情况为例，但是使用PyTorch来实现。

import numpy as np
import torch
from matplotlib import pyplot as plt
# 生成 输入数据x 及 目标数据y
np.random.seed(100)
x = np.linspace(-1,1,100).reshape(100,1)
y = 3*np.power(x,2)+2+0.2*np.random.rand(x.size).reshape(100,1)
x=torch.tensor(x)
y=torch.tensor(y)
# 查看x、y数据分布情况
plt.scatter(x,y)
plt.show()
# 初始化权重参数
w1 =torch.zeros(1,1,requires_grad=True)
b1 =torch.zeros(1,1,requires_grad=True)
# 训练模型
lr = 0.001 # 学习率
cost = []
for i in range(800): #梯度下降
    y_pred = w1*x**2 + b1
    loss = torch.sum((y_pred - y) ** 2)
    loss.backward()
    # 参数更新
    print(w1.grad.data.item(),b1.grad.data.item())
    # 梯度下降法
    w1.data = w1.data - lr*w1.grad.data  # 将学习率看作步长
    b1.data = b1.data - lr*b1.grad.data
    w1.grad.data.zero_()  #梯度清零
    b1.grad.data.zero_()

# 可视化结果
plt.plot(x,y_pred.data,'r-',label='predict')
plt.scatter(x,y,color='blue',marker='o',label='true') # true data
plt.xlim(-1,1)
plt.ylim(2,6)
plt.legend()
plt.show()
print(w1.data,b1.data)

数据和处理过程和前面都差不多，主要来看自动求导这块。首先在定义w1和w2的时候，w1 =torch.zeros(1,1,requires_grad=True)，意思是初试化1行1列的tensor w1初值为0，requires_grad默认值为false，赋值为True表示之后需要求解梯度

w1 =torch.zeros(1,1,requires_grad=True)
b1 =torch.zeros(1,1,requires_grad=True)

然后给出原始函数y_pred=w1 * x^2+b1，loss=Σ0.5*(y_pred - y)^2之后直接loss.backward()，表示从loss反向传播，计算loss到w1和b1的偏导，机器的具体计算过程可以参考计算图与自动求导，这样就不用手动计算对应的梯度公式，直接w1.grad.data.item()获得梯度的数值（w1.grad就可以获得梯度，但是得到的结果是一个tensor变量）
注意，每次循环都需要对梯度进行清零，否则每轮次梯度会累加前面的梯度，越算越大，与梯度下降的目的相悖

w1.grad.data.zero_()  #梯度清零

三、PyTorch神经网络工具箱

3.1 卷积神经网络层次

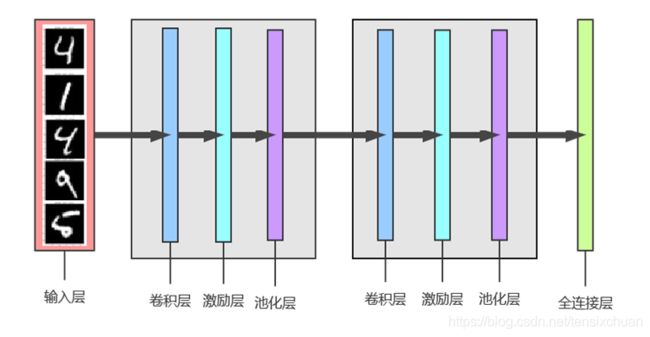
卷积神经网络是一种包含卷积计算操作且具有深度层次结构的前馈型神经网络，与传统神经网络的区别在于卷积神经网络的层和形式有了很大的变化，可以说是传统神经网络的一个改进。如下图所示，传统神经网络主要包括一个输入层、一个输出层，还有若干中间层，而卷积神经网络有许多传统神经网络没有的层次。

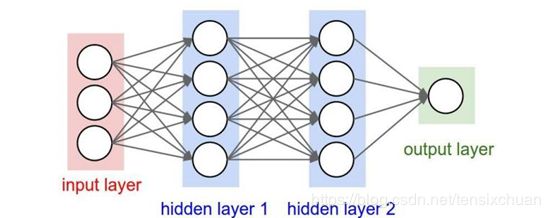
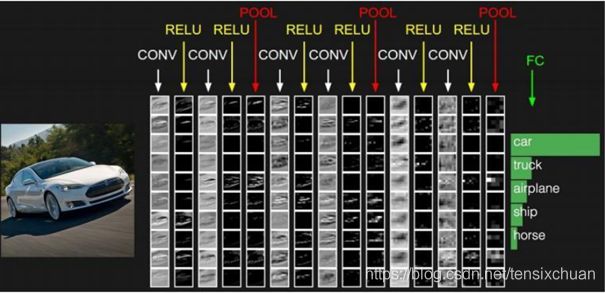
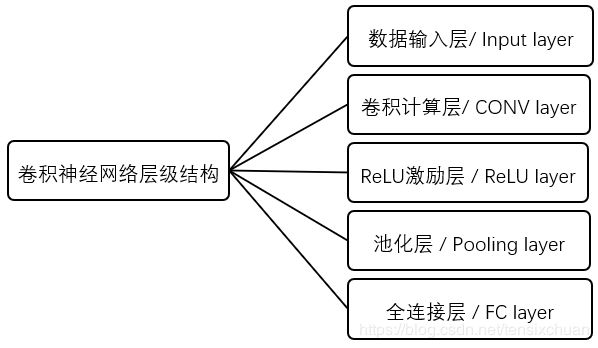
输入层也就是你喂进去的大量训练数据，所以主要介绍pytorch对其他几个层级的实现：

3.1.1 卷积层

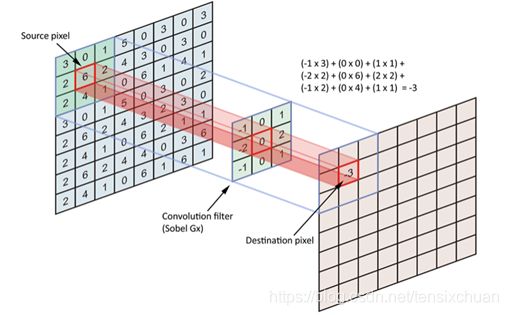
卷积计算层是卷积神经网络的核心层次，由若干卷积单元组成。在这个卷积层里，主要包含两个关键操作，一个关键操作是局部关联，它将每个神经元看做一个滤波器(filter)，另一个关键操作是窗口(receptive
field)滑动，让filter对局部数据计算。卷积计算层由若干卷积单元组成，每个卷积单元是一个权值矩阵，它会在二维的输入数据上每次滑动固定步长，然后将对应的窗口的元素值进行矩阵的乘法，把得到的计算结果输出到像素。
如图8就是一次卷积计算操作，其中左边的矩阵是初始输入的原始矩阵，中间矩阵为卷积核（filter），右侧是经过卷积计算后得到的输出值。通过卷积运算可以提取输入的不同特征，而且逐层加强，比如第一层卷积计算层可能只能提取低级特征，而更高层的网路可以从低级特征中迭代提取更为复杂的特征。

pytoch实现：

一维卷积： 多用于处理文本，只计宽度不计高度

conv1 = nn.Conv1d(in_channels=256, out_channels=100,
kernel_size=2)
input = torch.randn(32, 35, 256)
input = input.permute(0, 2, 1)
output = conv1(input)

二维卷积： 多用于处理图像

from PIL import Image
from torchvision.transforms
import ToTensor, ToPILImage
to_tensor = ToTensor()  # img ->tensor
to_pil = ToPILImage()  # tensor -> image
ll =Image.open('imgs/lena.png')  
input =to_tensor(lena).unsqueeze(0) 

3.1.2 激活层

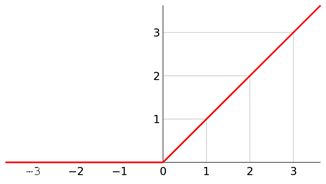
在神经网络中加入激活函数的话可以引入非线性因素，还能提高本模型的表达强度，缩小模型的训练时间，使训练成本下降，解决很多线性模型不能解决的问题。

pytoch实现 relu函数：

relu = nn.ReLU(inplace=True)
output = relu(input)
# output = input.clamp(min=0)

3.1.3 池化层

池化层（Pooling layer）本质上是采样操作，而上采样（upsampling）是将feature map还原，与上采样不同的是池化为下采样（subsampling）操作，一是压缩数据量，即压缩输入的特征图像来缩小图像尺寸来达到减小所需显存的目的；二是将feature map变小，即压缩输入的图像特征中的特征值减小计算量，去除特征值中重复冗余的信息以保留最主要的特征，改善过拟合的情况。

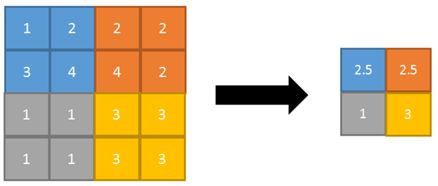
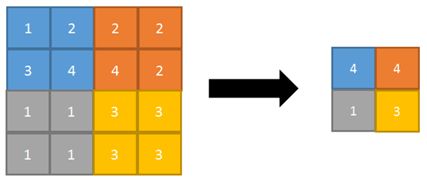
常见的池化操作包括平均池化（average
pooling）和最大池化（max pooling），其中平均池化是将图像区域的平均值当作该区域池化后的取值，平均池化能很好的保留背景但是会使图片变得模糊，而最大池化则是选取图像区域的最大值当作该区域池化后的取值，能比较好的保留图片纹理特征，一般来说最大池化比平均池化要更为常用。

平均池化：

最大池化：

pytoch实现：

pool1= nn.AvgPool2d(2,2)  # 平均池化
pool2= nn. MaxPool2d(2,2)  # 最大池化
out   = pool1( V(input) )
out   = pool2( V(input) )

3.1.4 全连接层（输出层）

在卷积神经网络中，经过多个卷积层和池化层后卷积神经网络的尾部一般会存在1个及以上的全连接层，主要负责与上一层的所有神经元进行全连接，整合卷积层和池化层中取得的局部特征以得到最终的特征图像。

pytoch实现：

input = V(t.randn(2,3))
linear = nn.Linear(3,4)
h = linear(input)

3.2 PyTorch搭建卷积神经网络——MNIST手写数字识别

接下来以mnist手写数字识别为例使用PyTorch神经网络工具箱搭建一个简单的卷积神经网络模型（完整代码在最后）

首先获取训练数据集

# 获取训练集dataset
training_data = torchvision.datasets.MNIST(
    root='./data/',  # dataset存储路径
    train=True,  # True表示是train训练集，False表示test测试集   
    transform=torchvision.transforms.ToTensor(),  # 将原数据规范化到（0,1）区间
    download=DOWNLOAD_MNIST,
)

# 打印MNIST数据集的训练集及测试集的尺寸
print(training_data.data.size())   # torch.Size([60000, 28, 28])
print(training_data.targets.size())   # torch.Size([60000])
# 打印一张看看长啥样
plt.imshow(training_data.data[0].numpy(), cmap='gray')
plt.title('simple')
plt.show()

#通过torchvision.datasets获取的dataset格式可直接可置于DataLoader
train_loader = Data.DataLoader(dataset=training_data,
batch_size=BATCH_SIZE,shuffle=True)

# 获取测试集dataset
test_data = torchvision.datasets.MNIST(root='./data/',train=False)

# 取前2000个测试集样本
test_x = Variable(torch.unsqueeze(test_data.data, dim=1),volatile=True).type(torch.FloatTensor)[:2000] / 255
# (2000, 28, 28) to (2000, 1, 28, 28), in range(0,1)
test_y = test_data.targets[:2000]

这是pytorch自带的数据集，图片长这样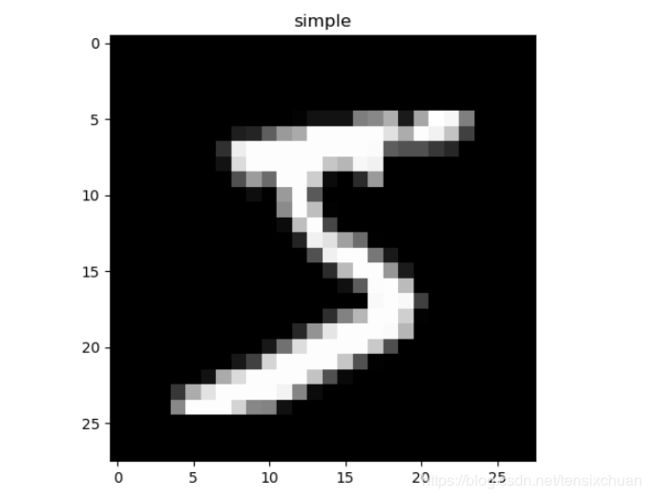
如果你没有mnist数据集的话它会给你自动下载，但是下载会很慢，所以可以自行下载之后新建data目录，然后把下载好的数据集放进去，节约时间

链接：https://pan.baidu.com/s/1TlvwqzkvfICdAceHITcMyw
提取码：u0nk

可以看到MNIST目录下有processed和raw两个目录，processed是用来放训练过程中产生的训练文件，不太用管，而raw目录才是存放训练图片的

然后设计cnn网络结构，定义一个具有如下结构的卷积神经网络

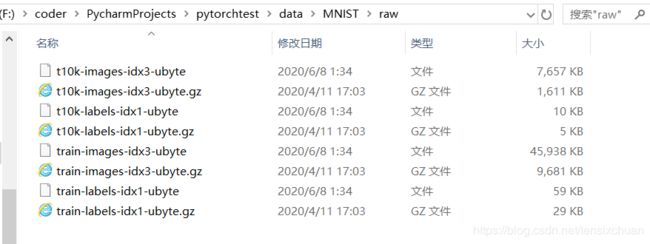
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(  # (1,28,28)
            nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5,
                      stride=1, padding=2),  # (16,28,28)
            # 想要con2d卷积出来的图片尺寸没有变化, padding=(kernel_size-1)/2
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2)  # (16,14,14)
        )
        self.conv2 = nn.Sequential(  # (16,14,14)
            nn.Conv2d(16, 32, 5, 1, 2),  # (32,14,14)
            nn.ReLU(),
            nn.MaxPool2d(2)  # (32,7,7)
        )
        self.out = nn.Linear(32 * 7 * 7, 10)

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = x.view(x.size(0), -1)  # 将（batch，32,7,7）展平为（batch，32*7*7）
        output = self.out(x)
        return output

拆开细看，定义的cnn整体结构：

CNN(
(conv1): Sequential(
(0): Conv2d(1, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(conv2): Sequential(
(0): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): ReLU()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(out): Linear(in_features=1568, out_features=10, bias=True)
)

其中一共有两大块——conv1、conv2

conv1包含一个二维卷积层：

nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5,
                      stride=1, padding=2),  # (16,28,28)

一个激励层：

nn.ReLU()

一个平均池化层：

nn.MaxPool2d(kernel_size=2)

而conv2同理。
最后是一个全连接层，也可以说是输出层

self.out = nn.Linear(32 * 7 * 7, 10)

而forward是原始的计算过程，之后可以用来反向传播

def forward(self, x):
    x = self.conv1(x)
    x = self.conv2(x)
    x = x.view(x.size(0), -1)  # 将（batch，32,7,7）展平为（batch，32*7*7）
    output = self.out(x)
    return output

这里的x相当于输入层，先把x放入第一块conv1（卷积——激励——池化），之后把输出结构再放入第二块conv2（卷积——激励——池化），再放入输出层out，最后返回输出结果output

3.3 模型训练与预测

训练搭建的网络并通过该模型来预测

先实例化刚刚设计的cnn网络cnn = CNN()，然后设置一个Adam优化器进行优化

optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)
loss_function = nn.CrossEntropyLoss()

循环训练

for epoch in range(EPOCH):
    for step, (x, y) in enumerate(train_loader):
        b_x = Variable(x)
        b_y = Variable(y)

        output = cnn(b_x)
        loss = loss_function(output, b_y)  #损失函数
        optimizer.zero_grad()   
        loss.backward()
        optimizer.step()

        if step % 100 == 0:
            test_output = cnn(test_x)
            pred_y = torch.max(test_output, 1)[1].data.squeeze()
            s1=sum(pred_y == test_y)
            s2=test_y.size(0)
            accuracy = s1/(s2*1.0)
            print('Epoch:', epoch, '|Step:', step,
                  '|train loss:%.4f' % loss.item(), '|test accuracy:%.4f' % accuracy)

其中optimizer.zero_grad()是清除之前的梯度，然后对loss调用backward()，最后，调用optimizer.step()将更新的值加到model的parameters上。
关于optimizer（torch.optim）的使用

每训练100次就输出当前的loss值和准确度，其中准确度accuracy = 预测结果和正确结果相同的总数/总数

Epoch: 0 |Step: 0 |train loss:2.3105 |test accuracy:0.0605
Epoch: 0 |Step: 100 |train loss:0.1290 |test accuracy:0.8735
Epoch: 0 |Step: 200 |train loss:0.4058 |test accuracy:0.9285
Epoch: 0 |Step: 300 |train loss:0.1956 |test accuracy:0.9440
Epoch: 0 |Step: 400 |train loss:0.1238 |test accuracy:0.9585
Epoch: 0 |Step: 500 |train loss:0.2217 |test accuracy:0.9630
Epoch: 0 |Step: 600 |train loss:0.0237 |test accuracy:0.9670
Epoch: 0 |Step: 700 |train loss:0.2158 |test accuracy:0.9700
Epoch: 0 |Step: 800 |train loss:0.0433 |test accuracy:0.9720
Epoch: 0 |Step: 900 |train loss:0.0564 |test accuracy:0.9770
Epoch: 0 |Step: 1000 |train loss:0.0320 |test accuracy:0.9760
Epoch: 0 |Step: 1100 |train loss:0.0233 |test accuracy:0.9825

可以看到梯度在不断下降，而准确度在不断增加。

然后拿训练好的模型进行预测

test_output = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')

for n in range(10):
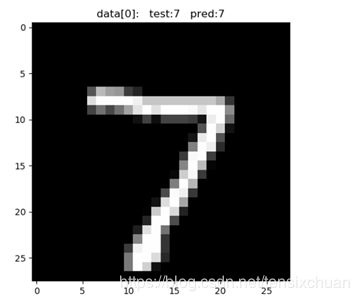
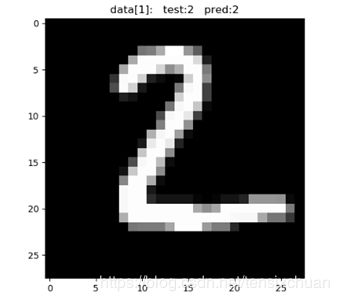
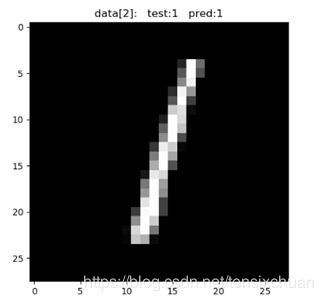
    plt.imshow(test_data.data[n].numpy(), cmap='gray')
    plt.title('data[%i' % n+']:   test:%i' % test_data.targets[n]+'   pred:%i' % pred_y[n])
    plt.show()

在测试集中拿出前10张图片放入训练好的网络中test_output = cnn(test_x[:10])（也可以裁取别的部分），获得预测值pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()，然后输出这10张图片的预测值和实际标签

结果：
[7 2 1 0 4 1 4 9 5 9] prediction number
[7 2 1 0 4 1 4 9 5 9] real number

同时还可以在图像中展示plt.imshow(test_data.data[n].numpy(), cmap='gray')

部分结果：

可以看到，识别的还是蛮准确的。

---

附：手写数字识别完整代码：

import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt

torch.manual_seed(1)

EPOCH = 1
BATCH_SIZE = 50
LR = 0.001
DOWNLOAD_MNIST = True

# 获取训练集dataset
training_data = torchvision.datasets.MNIST(
    root='./data/',  # dataset存储路径
    train=True,  # True表示是train训练集，False表示test测试集
    transform=torchvision.transforms.ToTensor(),  # 将原数据规范化到（0,1）区间
    download=DOWNLOAD_MNIST,
)

# 打印MNIST数据集的训练集及测试集的尺寸
print(training_data.data.size())
print(training_data.targets.size())
# torch.Size([60000, 28, 28])
# torch.Size([60000])
plt.imshow(training_data.data[0].numpy(), cmap='gray')
plt.title('simple')
plt.show()

# 通过torchvision.datasets获取的dataset格式可直接可置于DataLoader
train_loader = Data.DataLoader(dataset=training_data, batch_size=BATCH_SIZE,
                               shuffle=True)

# 获取测试集dataset
test_data = torchvision.datasets.MNIST(root='./data/', train=False)
# 取前2000个测试集样本

test_x = Variable(torch.unsqueeze(test_data.data, dim=1),
                  volatile=True).type(torch.FloatTensor)[:2000] / 255
# (2000, 28, 28) to (2000, 1, 28, 28), in range(0,1)
test_y = test_data.targets[:2000]


class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(  # (1,28,28)
            nn.Conv2d(in_channels=1, out_channels=16, kernel_size=5,
                      stride=1, padding=2),  # (16,28,28)
            # 想要con2d卷积出来的图片尺寸没有变化, padding=(kernel_size-1)/2
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2)  # (16,14,14)
        )
        self.conv2 = nn.Sequential(  # (16,14,14)
            nn.Conv2d(16, 32, 5, 1, 2),  # (32,14,14)
            nn.ReLU(),
            nn.MaxPool2d(2)  # (32,7,7)
        )
        self.out = nn.Linear(32 * 7 * 7, 10)

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = x.view(x.size(0), -1)  # 将（batch，32,7,7）展平为（batch，32*7*7）
        output = self.out(x)
        return output


cnn = CNN()
print(cnn)

optimizer = torch.optim.Adam(cnn.parameters(), lr=LR)
loss_function = nn.CrossEntropyLoss()

for epoch in range(EPOCH):
    for step, (x, y) in enumerate(train_loader):
        b_x = Variable(x)
        b_y = Variable(y)

        output = cnn(b_x)
        loss = loss_function(output, b_y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if step % 100 == 0:
            test_output = cnn(test_x)
            pred_y = torch.max(test_output, 1)[1].data.squeeze()
            s1=sum(pred_y == test_y)
            s2=test_y.size(0)
            accuracy = s1/(s2*1.0)
            print('Epoch:', epoch, '|Step:', step,
                  '|train loss:%.4f' % loss.item(), '|test accuracy:%.4f' % accuracy)

test_output = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')

for n in range(10):
    plt.imshow(test_data.data[n].numpy(), cmap='gray')
    plt.title('data[%i' % n+']:   test:%i' % test_data.targets[n]+'   pred:%i' % pred_y[n])
    plt.show()

---

参考资料：

莫烦python的CNN小实现
PyTorch 深度学习:60分钟快速入门（使用CIFAR10数据集实现图像分类）
基于PyTorch的深度学习入门教程（四）——构建神经网络
分别使用Numpy和Tensor及Antograd实现机器学习
基于PyTorch深度学习

---

我的汇报 ppt及演示代码

链接：https://pan.baidu.com/s/1vZUmWc3o6BZw_6B3ArvzlA
提取码：k0ap

链接：https://pan.baidu.com/s/1R9R_tYNerfbl71_WMZFS1w
提取码：0rtt

---

最后，码字不易，吐血整理的干货长文，如果有帮助的话可以点个赞呀，给你小心心~