球的体积交

题目链接：https://www.zhixincode.com/contest/10/problem/H?problem_id=153

题意：在三维坐标系中，有n个球体，每个球的球心为(xi,yi,zi)，半径为ri。再给定一个球（球心为(X,Y,Z)，半径为R），求该球与其余n个球相交部分体积。（保证一开始的n个球两两之间没有重叠）

先介绍球缺的概念：

球缺是指球体被平面截去一部分后剩余的部分。截面称为球缺的底面，垂直于截面的直径被此截面截得的线段长称为球缺的高。

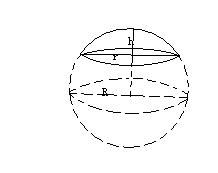
球缺的表面积：（R是球体的半径，h是球缺的高，r是球缺的底面半径）

球缺的体积： 或（R是球体的半径，h是球缺的高，r是底面半径）

与球冠区别：球缺是体，而球冠是面，故球冠只能计算表面积

后面附有大牛对球缺体积公式的证明

思路：
因为n个球两两之间没有重叠，所以考虑其中每个球(称为小球)与最后给定的那个球(称为大球)即可。分3种情况：

设 d 为两球球心之间的距离。

一、d >= R+ri ：两球不相交，即相交部分体积=0.

二、d+ri = R ：小球在大球里面，即相交部分体积 = 小球体积 =  .

三、R-ri < d < R+ri ：两球相交，相交部分体积：

设  ， .

， .

V =  .

证明：https://blog.csdn.net/luyehao1/article/details/86583384

 1 #include 
 2 using namespace std;
 3  
 4 typedef long long ll;
 5  
 6 const double pi = acos(-1);
 7  
 8 const int MAX = 100 + 10;
 9 const int inf = 1e9 + 7;
10  
11 typedef struct {
12     double x, y, z, r;
13 }Point;
14  
15 int n;
16 Point a[MAX];
17 Point s;
18  
19 //两点之间距离
20 double dis(Point p, Point q) {
21     double ans = sqrt((p.x - q.x)*(p.x - q.x) + (p.y - q.y)*(p.y - q.y) + (p.z - q.z)*(p.z - q.z));
22     return ans;
23 }
24  
25 int main()
26 {
27     int T;
28     scanf("%d", &T);
29     int Case = 1;
30     while (T--)
31     {
32         scanf("%d", &n);
33         for (int i = 0; i < n; i++) {
34             scanf("%lf%lf%lf%lf", &a[i].x, &a[i].y, &a[i].z, &a[i].r);
35         }
36         scanf("%lf%lf%lf%lf", &s.x, &s.y, &s.z, &s.r);
37         double ans = 0;
38         for (int i = 0; i < n; i++) {
39             double d = dis(s, a[i]);
40             if (d >= s.r + a[i].r) {
41                 continue;
42             }
43             else if (d + a[i].r <= s.r) {
44                 ans += (4.0 / 3)*pi*a[i].r*a[i].r*a[i].r;
45             }
46             else {
47                 double co = (s.r*s.r + d * d - a[i].r*a[i].r) / (2.0*d*s.r);
48                 double h = s.r*(1 - co);
49                 ans += (1.0 / 3)*pi*(3.0*s.r - h)*h*h;
50                 co = (a[i].r*a[i].r + d * d - s.r*s.r) / (2.0*d*a[i].r);
51                 h = a[i].r*(1 - co);
52                 ans += (1.0 / 3)*pi*(3.0*a[i].r - h)*h*h;
53             }
54         }
55         printf("Case #%d: %.10lf\n", Case++, ans);
56     }
57     return 0;
58 }

 

转载于:https://www.cnblogs.com/qingjiuling/p/10459877.html