为什么你只需要CD音质：16bits, 44.1kHz的意义

摘要

本文主要从音乐的存储和传输的角度探讨数字音乐体系的两大指标：采样频率和量化位数/深度的意义。为什么最初设计者选择的是44.1kHz和16bits的音乐记录标准？这两个数字背后的内涵是什么？作为拥有“金耳朵”的你，是否有必要选择追求更好的音质？如果你有如上的疑惑，那么本文或许对你有帮助。

尽管本文涉及的内容主要是高等院校的《信号与系统》和《数字信号处理》这两门课的内容，但笔者从科普角度出发，分享一下自己的见解。希望你在阅读后有所收获。

本文由@EthanLifeGreat原创发表于CSDN，转载请注明出处.

前言

音频的存储是一门复杂的学问。用数字记录声音面临着一大问题——速度与精度的权衡。如果用少量的信息存储声音，那么音频传输的速率会提高；而如果用大量的信息记录，精度就会下降。

实用主义的思想要求我们找到人耳对声音的最高分辨能力。并据此设计出合适的音质，以至于其信息量不大而又能让你听不出来问题。

本文主要从实用角度阐述CD音质(16bits, 44.1kHz)的必要性和充分性。

• 在第二章，我们介绍数字音频存储中的相关概念。
• 第三章我们介绍(44.1kHz)采样频率的意义。
• 第四章我们解析(16bits)量化的内涵。
• 最后一章我们简要总结全文并延申相关知识。

铺垫：用初中数学理解音乐存储

在自然世界里，只有模拟信号(Analog Signal)。模拟信号，其实”模拟“的就是自然世界里的事情。
学过初中物理的我们知道，如果你用麦克风记录你的歌喉，实际上是麦克风上的振动膜被你的声带带着振动。如此的振动，在时间上是连续的。

实际上，这些振动可以看成是一个关于时间的连续函数。而学过初中数学的我们直到，函数的表示方法只有三种：_______ 、_______ 和 ________¹。 (你上网课上疯了？)

我们先讲解析式法：因为自然世界中的声音千奇百怪，你并不总能找到一个能对应你要记录的声波的解析式，所以我们第一个抛弃这种想法²。

但是图像法和列表法却都被我们采用过：

图像法：最早记录声音的是爱迪生的留声机，它的本质原理可以看成是图像法——把声音（振动）刻在盘子（唱片）上。然后读取的时候再把唱针放在唱片上读出原来的振动。

（图源百度图片，希望没有侵权）

列表法：我们知道列表法的缺点是列出来的点总是有限的，也就是你再怎么列点，也只是取了整个函数的很小一部分。但是，只要功夫深，我们就能让人有一种”嗯~，确实是连续的“感觉。

这样，我们就引出了信号与系统中的“列表法”——采样(Sampling)。所列表中的每一列，就是一个采集到的“样”。
列表法的结果也就是我们的数字信号(Digital Signal)，我们存储这些数量庞大的离散的数值，来记录声音的形状。

下一章我们讲讨论列表法到底要列几个点，也即采样频率。

采样频率44.1kHz：听到你生命中最高亢的部分

采样频率(Sampling Frequency)是一个老生常谈的话题了。

为了使数据量尽可能小，我们希望每秒钟采集的信号数尽可能少³；但是，我们还得同时保证采集出来的样本数尽可能多，以维持信号的完整性。

我们在这里讨论完整性时，我们更多的是讨论高频信号的保留度⁴——如果你的采样频率过低，你会将一个高频信号认成低频信号。设想一个例子：你的采样频率是80Hz，也就是说你每1/80秒就观察一次这个模拟信号并记录它的值。但是你采样的目标里有一个频率为81Hz的信号。通俗地讲就是，当你下一眼看回来的时候，这个信号已经跑了一圈多一点了，但你会觉得它只跑了一点点（1/80圈）⁵。

如下图是一个本为81Hz但在80Hz采样频率下被当作是1Hz的信号：

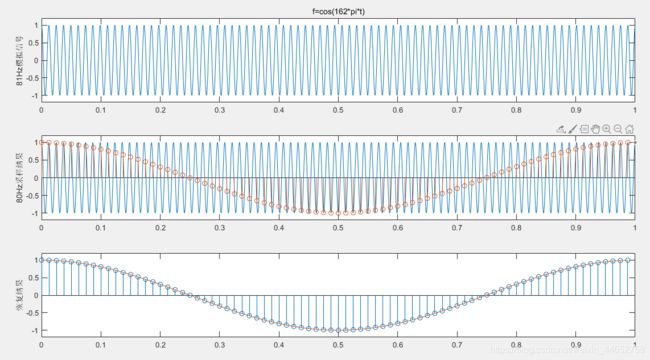
这样一来，我们必须舍去高于采样频率的信号，因为我们不能将它与频率内的信号区分开来。故在实操中，我们用低通滤波器(Low-pass Filter)先对模拟信号滤波，丢掉会混进低频部分的高频信号，再进行采样。

值得一提的是，新竹清华大学的刘奕汶教授称这种现象或可用作“传音入密”。即当信号的频率范围不确定的时候，被滤波器过滤的信号其实可能暗藏着真正的信息。

至此为止，我们只说明了：采样频率必须不小于信号中最高的频率。
然而，奈奎斯特采样定理(Nyquist’s Sampling Thereom)告诉我们，要完整地恢复信号，（更严格地，）采样频率还必须大于信号中最高频率的两倍。

奈奎斯特定理表示，如果被采样信号中有大于采样频率一半的信号，那么它们也会被重构成低于采样频率一半的信号，这种现象被称为“混叠”。（前面81Hz的例子也属于混叠⁶）。

我们都知道人的听觉范围是20Hz~20,000Hz，也即我们无法听到频率高于2万赫兹的声音。所以这个上限乘上两倍（再加上一些冗余，）就得到了我们的44100Hz. 所以理论上讲，这个采样频率保留了你生命中能听见的最“高亢”的部分（或者是最尖锐的部分，这取决于你怎么理解）。

另外，为了保证通话顺畅，电话一般是采用8kHz的采样频率。注意，键盘上的大字组C8（88键钢琴最高音）的频率是4186Hz. 鉴于你一般不会在电话里唱海豚音，工程师们认为8000的采样频率足够了。

尽管有学者认为人听不见的高频率也会对音质产生影响，但实打实地说，一般认为保留住 22.05kHz（44.1kHz / 2）的频率足够保证音质优秀了。

量化位数16bits：保证最纯净的音乐

学过大学计算机（基础）的我们知道，比特(bit)的意思是0或1中的一种取值，是信息量的单位。每多一个比特，意味着信息量就翻了一番。

但为什么音乐的存储要用到比特？我们之前说声音是时间的连续函数，也就是说值域是连续的，其值有可能取到任何的有理数/无理数。但是计算机存储数据是必须要离散的，例如：C语言的int，float，double；Matlab的Single，Double等。这些存储格式都有各自的比特数，如，float 32bits; double 64bits 等。这就相当于在数轴上画上了刻度（$n$个bits对应$2^n$个刻度），计算机里的数字只能在这些刻度上取。

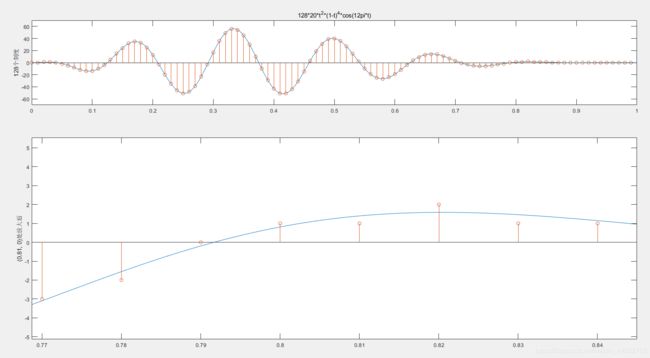
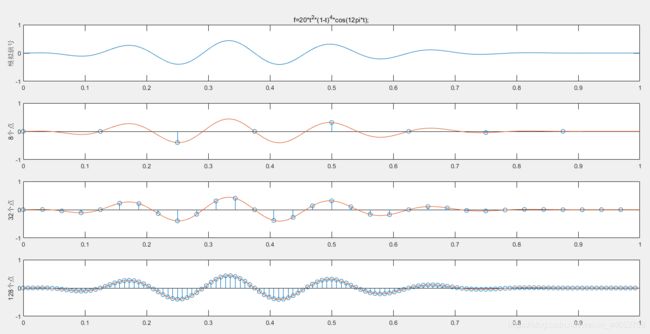
而把信号中连续的取值强行“掰”到给定的刻度上，就要求我们四舍五入。这个过程叫做量化(Quantization). 例如，我们用8个bits=128个刻度来刻画一个信号，如图：

四舍五入丢掉的精度，就是量化过程产生的噪声。

我们回顾一下刚才那张图里四舍五入舍去的数值：

注意，因为四舍五入的原理，这里的纵坐标是-0.5到0.5之间。

反过来理解，量化得到的结果就是：把上面这张图的数值取相反数后加在原信号上。其本质就是噪声⁷。

那么问题来了：我们需要精确到多少以保证噪声很小（以至于实际上我们没法听见）呢？

这里我们要引入分贝(dB)的概念。

分贝

分贝(dB)本质上是一个比值，衡量两个单位相同的数字之间的关系。比如当我们说小区里的噪音有32分贝，意思就是说噪声比我们能听见的最小声音高32个标准。

接下来我们定义这个标准：
声音的本质是振动，音量取决于振幅。为了使数字更好看，科学家们将两种声波振幅的比值按以下公式写成分贝数：

$$dB=20\ast lo{g}_{10}\frac{A1}{A2}$$

其中A1和A2分别是两个声音的振幅，且有A1大于等于A2。
所以如果两个声音的音量相同，我们会用0dB来表示。

据美国职业安全卫生管理局(OSHA)规定，人耳最大可以承受连续8小时85分贝的声音强度，而无负面影响。就是说，我们可以近似认为人可以长时间听比自己刚好听不见的声音大85分贝的声音。

所以，我们的音乐设计标准就是，让量化噪音比播放器的最大声音小85分贝以上⁸。接下来的重点是揭示量化位数和噪音分贝数的关系。

噪音和量化位数的关系

先上结论：每增加1个比特的量化位数则噪音(相对最大音量)减少6dB

证明：不难看出，每增加1个比特的量化位数，则信息量翻一番，量化误差缩小一半。即噪音振幅缩减为原来的一半。故在最大音量不变的情况下，根据上面对分贝的定义，每增加1个比特，噪音会减小6dB。

接着用数学归纳法：如果只用1个比特来表示振幅，那么误差最大是最大振幅的一半，即噪音只比真实信号低6dB。得到如果总共使用16 bits进行量化，噪音将比乐音小96dB。

换言之：能忍受96dB的乐音的你，才刚好能听见量化噪音。

总结

在本文里，我们讨论了CD音质两个标准和其存在的意义：

• 采样频率：保留高音
• 量化位数：降低噪音

而对于绝大多数人而言，44.1kHz 和 16bits 这两项标准已经能达到纯净音乐的标准了。

通过简单的计算我们我们就知道这个标准每秒钟需要传送的信息，即比特率是：44.1kHz * 16bits * 2 channels = 1411.2 kbps. 换算成网速常用的表示就是 176.4 kB/s.

尽管这个信息量并不算大，但是对于速度的追求是无止境的~ 科学家和工程师们研究了许多有损和无损的压缩方法，将音频压缩到更低的比特率⁹。

所以我们的结论是：对于一般人，CD音质足以达到“好音乐”的标准。

---

1. 列表法、解析式法和图象法。 ↩︎

2. 或许有人采用过这种办法。如果你知道，欢迎提出。 ↩︎

3. 每秒钟某事发生的次数定义为赫兹(Hz)。如果每秒钟采样八千次，那么采样频率就是8kHz。 ↩︎

4. 也可能采样频率低会导致除高频信号消失以外的其它问题。但为了使逻辑顺畅，我们暂且认为采样频率低仅会导致高频信号消失。 ↩︎

5. 你没有理由觉得它真的跑了一圈多一点，如果你这么认为的话，它也可能是跑了两圈多一点或者更多……所以只能认为它没跑到一圈，否则你没办法区分它跑了几圈。 ↩︎

6. 前面81Hz的例子非常浅显，是因为原信号（81Hz）和混叠出的信号（1Hz）除了频率不同外，相角和振幅都没变。但是低于采样频率（但高于其一半）的信号的混叠会使相角和振幅都改变。这就使得这样的混叠不能直观地表达，也使证明难度增加 ↩︎

7. 如果你了解白噪声的话，你就知道这就是分布在(-0.5, 0.5)之间的噪声。 ↩︎

8. 如果你了解信噪比(SNR)，你就会知道这里的噪音小85dB，意味着信噪比是85dB。但为了便于解释， ↩︎

9. 其中就有我们熟知的MP3有损压缩技术，MP3技术进行压缩后，典型的比特率介于128kbps和320kbps（kbit/s）之间。故对比CD音质的1411.2kbps的信息率，压缩比可以大于10. ↩︎