编写立方体的一点透视投影图

一.窗口到视区的坐标变换
1.窗口：在世界坐标系中，设置一矩阵区域，来观察整幅图中的部分内容。

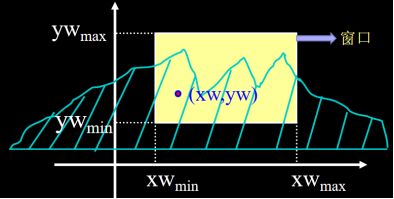
2.视区：窗口映射到显示器上的区域称为视区。

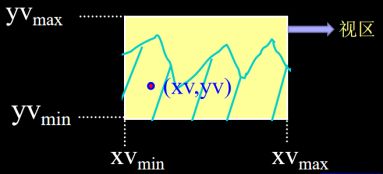
3.坐标变换

(xv-xv_min)/(xv_max-xv_min)=(xw-xw_min)/(xw_max-xw_min)
(yv-yv_min)/(yv_max-yv_min)=(yw-yw_min)/(yw_max-yw_min)    **[(xv,yv)为视区中的坐标]**

转化为：

xv=xv_min+(xw-xw_min)Sx
yv=yv_min+(yw-yw_min)Sy

其中缩放因子Sx,Sy：

Sx=(xv_max-xv_min)/(xw_max-xw_min)
Sy=(yv_max-yv_min)/(yw_max-yw_min)      **[当Sx=Sy，物体保持相似性]**

二．一点透视投影
1.透视投影
透视投影的视线（投影线）是从视点（观察点）出发，视线是不平行的。模拟人眼观察物体的过程。透视图是通过透视中心（视点），将空间立体投影到二维平面（投影面）所产生的图形，具有较强的立体感。

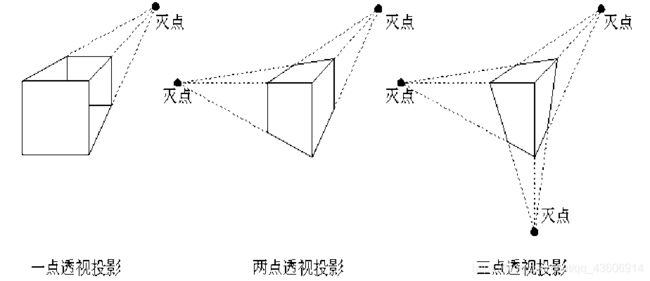
2.一点透视
不平行于投影平面的平行线汇聚的一点称为灭点，在坐标轴上的灭点叫做主灭点。主灭点数和投影平面切割坐标轴的数量相对应。一点透视即有一个主灭点Z_prp。

3.透视变换方程的推导
（1）坐标为(x,y,z)的P点到观察平面上点(xp,yp,zp)的透视投影。

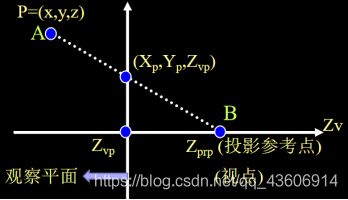
这里，直线AB的参数化方程：

     x’=x-xu ①
     y’=y-yu ②
     z’=z-(z-z_prp)u ③
     u∈[0,1]

我们可通过③式得到u值求解①②：
当u=0,位于P=(x,y,z)处；u=1,位于投影参考点(0,0,z_prp)处
在观察平面上，z’=z_vp（z_vp是投影平面在Z轴的截距）

z_vp=z-(z-z_prp)u 
u=(z-z_vp)/(z-z_prp)

将u值代入x’和y’的方程，得到透视变换方程：

xp=x[(z_prp-z_vp)/(z_prp-z)]=x *dp/(z_prp-z)
yp=y[(z_prp-z_vp)/(z_prp-z)]=y *dp/(z_prp-z)

其中， dp= z_prp-z_vp是投影参考点到观察平面的距离
这里代码中直接设置z_vp =0，则

xp=x* z_prp/(z_prp-z)=x *1/( 1-z/z_prp)
yp=y* z_prp/(z_prp-z)=y *1/( 1-z/z_prp)

三.主要步骤
1.确定空间坐标系中八个点坐标（数组存放）;

2.确定立方体各顶点的投影坐标（这里z_vp=0，即投影在xoy面）;

xp=x* z_prp/(z_prp-z)=x *1/( 1-z/z_prp)
yp=y* z_prp/(z_prp-z)=y *1/( 1-z/z_prp)

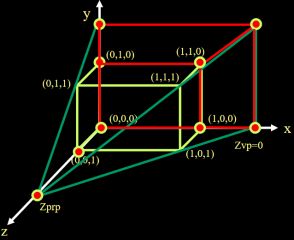
图中红线即得到的投影区域（其中有重合点），这样得到的图形没有立体感，所以可以在最初设置x和y的平移量使之有立体感

3.将投影坐标变换到屏幕上，最后连线即可。

xv=xv_min+(xw-xw_min)Sx
yv=yv_min+(yw-yw_min)Sy
Sx=(xv_max-xv_min)/(xw_max-xw_min)
Sy=(yv_max-yv_min)/(yw_max-yw_min)

代码如下：

#include
#include

float xt,yt,d;//xt,yt为平移量，d为视点z_prp坐标 

void Perspect(float *p){	
	//确定立方体各顶点的投影坐标 
	for(int i=0;i<24;i=i+3){
		p[i]=(p[i]+xt)/(1-p[i+2]/d);
		p[i+1]=(p[i+1]+yt)/(1-p[i+2]/d);
		p[i+2]=0;
	}
	// 得到窗口中xp_min xp_max yp_min yp_max
	float xp_min=p[0];
	float xp_max=p[3];
	for(int i=0;i<24;i=i+3){
		if(p[i]<=xp_min)
			xp_min=p[i];
		else
			xp_max=p[i];
	}
	
	float yp_min=p[1];
	float yp_max=p[4];
	for(int i=1;i<24;i=i+3){
		if(p[i]<=yp_min)
			yp_min=p[i];
		else
			yp_max=p[i];
	}
	//窗口到视区的坐标变换 
	float xv_min=20;
	float xv_max=45;
	float yv_max=20;
	float yv_min=45;
	
	float Sx=(xv_max-xv_min)/(xp_max-xp_min);
	float Sy=(yv_max-yv_min)/(yp_max-yp_min);
	for(int i=0;i<24;i=i+3){
		p[i]=xv_min+(p[i]-xp_min)*Sx;
		p[i+1]=yv_min+(p[i+1]-yp_min)*Sy;
		p[i+2]=0;
	}
	for(int i=0;i<24;i++){
		p[i]=(int)p[i];
	}
	int p1[10]={p[0],p[1],p[3],p[4],p[15],p[16],p[12],p[13],p[0],p[1]};
	int p2[10]={p[6],p[7],p[9],p[10],p[21],p[22],p[18],p[19],p[6],p[7]};
	//连线 
	drawpoly(5,p1);drawpoly(5,p2);
	line(p[0],p[1],p[9],p[10]);
	line(p[3],p[4],p[6],p[7]);
	line(p[15],p[16],p[18],p[19]);
	line(p[12],p[13],p[21],p[22]);
}

int main(){
	initgraph(640,480);
	setbkcolor(BLACK);
	float p[24]={0,0,0,1,0,0,1,1,0,0,1,0,0,0,1,1,0,1,1,1,1,0,1,1};
	printf("输入平移的位置：\n");
	printf("xt= ");scanf("%f",&xt);
	printf("yt= ");scanf("%f",&yt);
	printf("输入视点z_prp：\n");
	printf("d= ");scanf("%f",&d);
	Perspect(p);
	getch();
	closegraph();
	return 0;
}