iClient for OpenLayers求随机点的包围线（凸包）

iClient for OpenLayers求随机点的包围线（凸包）

作者:yangjl

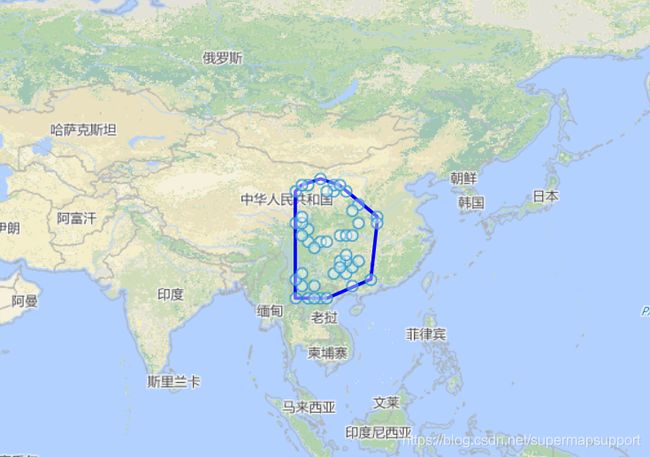
就在上个星期，有两位客户小伙伴问我如何取得任意随机的最外围的极端点，并使矢量线将其包围。其实这个问题是比较经典的一种计算几何的概念–凸包。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。凸包最常用的凸包算法是Graham扫描法和Jarvis步进法。这次我选取比较容易理解，且网上解释较多的Graham扫描法作为算法，结合iClient for OpenLayers地图框架，实现凸包展示。。

总体步骤：

1. 利用距离查询，查询出一定距离的要素点
2. 利用Graham算法，传入要素的坐标组
3. 拿取返回的点数组，构建几何线

开发准备：

本次功能的实现，需要了解凸包中的Graham扫描法，以及iClient for OpenLayers相关知识

1. Graham扫描法相关技术参考链接地址:：
   https://www.cnblogs.com/aiguona/p/7232243.html.
2. iClient for OpenLayers产品的开发指南链接地址:
   http://iclient.supermap.io/web/introduction/openlayersDevelop.html.

代码实现:

为代码简洁实现利用CDN在线引入iClient for OpenLayer文件，进行单网页的开发。
具体步骤如下：

1. 引入js库

<link href="https://cdnjs.cloudflare.com/ajax/libs/openlayers/4.6.5/ol.css" rel="stylesheet" />
<link href='http://iclient.supermap.io/dist/openlayers/iclient-openlayers.min.css' rel='stylesheet' />
<script type="text/javascript" src="https://cdnjs.cloudflare.com/ajax/libs/openlayers/4.6.5/ol.js"></script>
<script type="text/javascript" src="http://iclient.supermap.io/dist/openlayers/iclient-openlayers.min.js"></script>

2. 加载地图

map = new ol.Map({
        target: 'map',
        controls: ol.control.defaults({attributionOptions: {collapsed: false}})
            .extend([new ol.supermap.control.Logo()]),
        view: new ol.View({
            center: [100, 0],
            zoom: 3,
            projection: 'EPSG:4326'
        })
    });
    var layer = new ol.layer.Tile({
        source: new ol.source.TileSuperMapRest({
            url: url,
            wrapX: true
        }),
        projection: 'EPSG:4326'
    });
    map.addLayer(layer);

3. 进行地图的距离查询，查询出周围的点

      var param = new SuperMap.QueryByDistanceParameters({
           queryParams: {name: "[email protected]"},
            distance: 10,
            geometry: point
        });
        //创建距离查询实例
     New ol.supermap.QueryService(url).queryByDistance(param, function (serviceResult) {
       Var fes=serviceResult.result.recordsets[0].features.features; 
}) 

4. 定义 传入坐标数组、长度，以及结果数组变量，然后将传入的坐标数组构造完成

	              var res=new Array();//结果数组坐标点
              var p=new Array();//传入数组坐标点
              var n=fes.length //传入数组长度
    for(var i=0;i<fes.length;i++)
    {
        p[i]=new Object();
        p[i].x=fes[i].geometry.coordinates[0]
        p[i].y=fes[i].geometry.coordinates[1]
        p[i].tj=false
    }
     console.log(p,n) 

5. 定义Graham扫描法函数，这里就直接引用网上的步骤说明，引自:
   https://www.cnblogs.com/aiguona/p/7232243.html.
   1、先将点按从下向上，从左向右的顺序排序。排完序的第一个点，一定为凸包上的点，记为P0。
   2，计算各个点相对于 P0 的幅角 α ，按从小到大的顺序对各个点排序。当 α 相同时，距离 P0 比较近的排在前面。我们由几何知识可以知道，结果中第一个点 P1 和最后一个点一定是凸包上的点。
   （以上是准备步骤，以下开始求凸包）
   3、将p0、p1放进栈里，从p2开始为当前点，开始求凸包，找第三个点。
   4.连接P0和栈顶的那个点，得到直线 L（方向由p0指向栈顶那个点） 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5；如果在直线上，或者在直线的左边就执行步骤6。
   5.如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤4。
   6.当前点是凸包上的点，把它压入栈，执行步骤7。
   7.检查当前点 P 是不是最后一个点，是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点，返回步骤4。
   最后，栈中的元素就是凸包上的点了。

详细代码:

function multiply(p0,p1,p2){
    return((p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y)); 
}   //相乘
function distance_no_sqrt(p1,p2)
{
    //return(sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y))); 
    return((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)); 
}
function Graham_scan(pointSet,ch,n){

// 这里会修改pointSet
    var i,j,k=0,top=2;
    var tmp=new Object();
    // 找到一个基点，基本就是保证最下面最左面的点
    for(i=1;i<n;i++){
        if( (pointSet[i].y<pointSet[k].y) || 
            ( (pointSet[i].y==pointSet[k].y) && (pointSet[i].x<pointSet[k].x) ) 
          ){
            k=i;
        }
    }
    //这个点作为基点
    tmp=pointSet[0];
    pointSet[0]=pointSet[k];
    pointSet[k]=tmp; 

    use=n;
    for (i=1;i<use-1;i++){
        k=i;
        for (j=i+1;j<use;j++){
            var direct=multiply(pointSet[0],pointSet[k],pointSet[j]);
            if(direct>0){
                k=j;
            }else if(direct==0){
                // k j 同方向
                var dis=distance_no_sqrt(pointSet[0],pointSet[j])-distance_no_sqrt(pointSet[0],pointSet[k]);
                use--; // 也就是不要了
                if(dis>0){
                    // 保留j
                    // 把 k 就不要了
                    pointSet[k]=pointSet[j];
                    pointSet[j]=pointSet[use];
                    j--;
                }else{
                    tmp=pointSet[use];
                    pointSet[use]=pointSet[j];
                    pointSet[j]=tmp;
                }
            }
        }
        tmp=pointSet[i];
        pointSet[i]=pointSet[k];
        pointSet[k]=tmp;
    }

    ch.push(pointSet[0]);
    ch.push(pointSet[1]);
    ch.push(pointSet[2]);
    for (i=3;i<use;i++){
        while ( !(multiply(pointSet[i],ch[top-1],ch[top]) < 0 ) ){
            top--;
            ch.pop();
        }
        top++;
        ch.push(pointSet[i]);
    }
    return ch;
}

6. 最后将返回的结果数组，构造成ol.geom.LineString()所需传入的points数组，然后通过vectorlayer展示在地图上

 var points=Graham_scan(p,res,n) //进行凸包算法
    var poin=[];
    console.log(points.length,"len")
    for(var j=0;j<points.length;j++)
    {
       var a=new Array();
        a[0]=points[j].x;
        a[1]=points[j].y;
        poin.push(a)
    }
    poin.push(poin[0])
    console.log(poin,"a")
    
    
        var  roadLine = new ol.geom.LineString(poin);

        var Source = new ol.source.Vector({
            features: [new ol.Feature(roadLine)]
        });
        var Layer = new ol.layer.Vector({
            source: Source,
            style: new ol.style.Style({
                stroke: new ol.style.Stroke({
                    color: 'blue',
                    width: 3
                }),
                fill: new ol.style.Fill({
                    color: 'rgba(0, 0, 255, 0.1)'
                })
            })
        });
        map.addLayer(Layer);

效果展示

结果随机点的包围线，