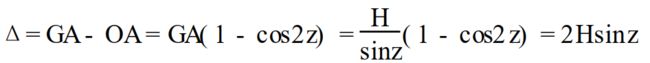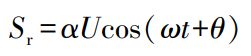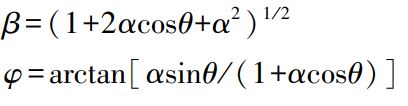卫星导航定位误差之多路径&地球自转&相位缠绕&相位中心误差
一、多路径
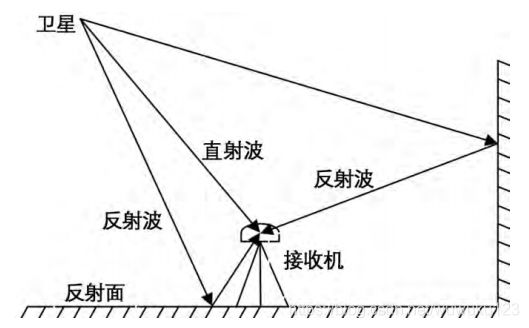
在GNSS测量中,被测站附近的反射物所反射的卫星信号(反射波)如果进入接收机天线,就将和直接来自卫星的信号(直射波)产生干涉,从而使观测值偏离真值,产生所谓的“多路径误差”。这种由于多路径的信号传播所引起的干涉时延效应被称做多路径效应。
1、反射波对直射波/信号的影响
实际测量中,GNSS天线接收到的信号是直射波和反射波发生干涉后的组合信号。反射物可以是地面、山坡和测站附近的建筑物等。现以地面为例来加以说明。若接收天线同时收到了直接来自卫星的信号S和经地面反射后的反射信号S′,显然这两种信号所经过的路径长度是不同的,反射信号多经过的路径长度称为程差,用Δ表示。下图所示:
式中,H为天线离地面的高度。由于存在着波程差Δ,所以反射波和直射波间存在一个相位延迟θ(以弧度为单位),如下,其中λ为载波波长;
因此,反射波信号北接收机接收时,会出现两个现象:
1、相位延迟;
2、信号强度降低;
将反射物发射信号的能力用反射系数α表示;
α=0表示信号完全吸收,不反射;
α=1表示信号完全发射,不吸收;
公式表示如下:
直射波信号表达式为:U为信号电压,w为载波的角频率;
反射信号表达式为:
U 为直接信号的振幅,ω 为载波卫星的角频率,θ 为反射信号的相位延迟,α 为物体的反射系数。 由于卫星接收的是反射信号和直接信号的叠加信号,所以天线实际接收的信号为:![]()
β、φ为:
φ即为多路径误差。当有多个反射信号同时进入接收机天线时,此时的多路径误差为:
2、消除和削弱多路径误差的方法和措施
1、选择合适的站址
2、选择合适的GNSS接收机
- 在天线下设置抑径板或抑径圈;
- 接收机天线对极化方向相反的反射信号应有较强的抑制能立;
- 改进接收机的软、硬件;
3、适当延长观测时间
二、地球自转校正
简单说,一般情况下,我们解算的坐标系为ECEF或BLH,两个坐标系都不是惯性坐标系,都收到地球自转的影响;计算卫星位置的时刻,是卫星信号发射的时刻/Ts;求解接收机位置的时刻,是接收到卫星导航信号的时刻/Tr;
Ts+传输时间=Tr;因此,Tr时刻的ECEF与Ts时刻的ECEF,发生了传输时间的转动,因此,需要将卫星位置做相应的变动,才能够准确计算的接收机位置。
以RTKLIB中,计算卫星、接收机几何距离代码为例:
/* geometric distance ----------------------------------------------------------
* compute geometric distance and receiver-to-satellite unit vector
* args : double *rs I satellilte position (ecef at transmission) (m)
* double *rr I receiver position (ecef at reception) (m)
* double *e O line-of-sight vector (ecef)
* return : geometric distance (m) (0>:error/no satellite position)
* notes : distance includes sagnac effect correction
*-----------------------------------------------------------------------------*/
//计算卫星和当前接收机位置之间的几何距离和 receiver-to-satellite 方向的单位向量。
extern double geodist(const double *rs, const double *rr, double *e)
{
double r;
int i;
if (norm(rs,3)三、天线相位缠绕
相位缠绕(Phase Wind-Up)是发射端与接收端之间的相对运动导致的载波相位变化。对 GPS 系统来说,因为 GPS 卫星发送的是右旋圆极化(RHCP: Right Hand Circularly Polarized)的信号,在这种情况下,接收机或者卫星天线的旋转会导致载波相位发生改变,这个值可能达到一个载波周期,我们把这种现象叫做相位缠绕。
接收机端由于载体/接收机的运动导致的旋转/相位缠绕被接收机钟差吸收掉;因此,在PPP中不予以考虑,只考虑卫星端的相位缠绕。
所幸相位缠绕只影响载波相位测量,不影响码相位测量,在非精密定位中可以忽略其影响。对差分定位来说其影响一般也可以忽略,尤其是短基线的时候。然而对精密单点定位来说,其影响就不能忽略了,因其影响可能会达到分米级。
下面介绍常用的相位缠绕模型。
如下图所示是卫星、地球与太阳的位置关系:
在 RTKLIB 中是通过调用model_phw 函数来进行相位缠绕校正的。此函数的计算过程同上述模型几乎完全一致,这里附上代码,过程很直接,就不多解释了。/函数对卫星端和接收机端都进行了校正。
/* phase windup model --------------------------------------------------------*/
static int model_phw(gtime_t time, int sat, const char *type, int opt,
const double *rs, const double *rr, double *phw)
{
double exs[3],eys[3],ek[3],exr[3],eyr[3],eks[3],ekr[3],E[9];
double dr[3],ds[3],drs[3],r[3],pos[3],cosp,ph;
int i;
if (opt<=0) return 1; /* no phase windup */
/* satellite yaw attitude model */
if (!sat_yaw(time,sat,type,opt,rs,exs,eys)) return 0;
/* unit vector satellite to receiver */
for (i=0;i<3;i++) r[i]=rr[i]-rs[i];
if (!normv3(r,ek)) return 0;
/* unit vectors of receiver antenna */
ecef2pos(rr,pos);
xyz2enu(pos,E);
exr[0]= E[1]; exr[1]= E[4]; exr[2]= E[7]; /* x = north */
eyr[0]=-E[0]; eyr[1]=-E[3]; eyr[2]=-E[6]; /* y = west */
/* phase windup effect */
cross3(ek,eys,eks);
cross3(ek,eyr,ekr);
for (i=0;i<3;i++) {
ds[i]=exs[i]-ek[i]*dot(ek,exs,3)-eks[i];
dr[i]=exr[i]-ek[i]*dot(ek,exr,3)+ekr[i];
}
cosp=dot(ds,dr,3)/norm(ds,3)/norm(dr,3);
if (cosp<-1.0) cosp=-1.0;
else if (cosp> 1.0) cosp= 1.0;
ph=acos(cosp)/2.0/PI;
cross3(ds,dr,drs);
if (dot(ek,drs,3)<0.0) ph=-ph;
*phw=ph+floor(*phw-ph+0.5); /* in cycle */
return 1;
}四、相位中心误差
1、天线高改正
即地面标示到天线参考点的向量
对应Rinex文件头中
0.0000 0.0000 0.0000 ANTENNA: DELTA H/E/N对应RTKLIB中变量类型为;
double antdel[2][3]; /* antenna delta {{rov_e,rov_n,rov_u},{ref_e,ref_n,ref_u}} */2、天线相位中心参考点/PCO
3、天线相位中心变化/PCV
RTKLIB中天线改正模型,相关的代码:
typedef struct { /* antenna parameter type */
int sat; /* satellite number (0:receiver) */ //设置卫星的号码,0代表接收机。
char type[MAXANT]; /* antenna type */
char code[MAXANT]; /* serial number or satellite code */
gtime_t ts,te; /* valid time start and end */
double off[NFREQ][ 3]; /* phase center offset e/n/u or x/y/z (m) */
double var[NFREQ][19]; /* phase center variation (m) */
/* el=90,85,...,0 or nadir=0,1,2,3,... (deg) */
} pcv_t;off为相位中心偏移;
var为相位中心变化;
/* receiver antenna model ------------------------------------------------------
* compute antenna offset by antenna phase center parameters
* args : pcv_t *pcv I antenna phase center parameters
* double *azel I azimuth/elevation for receiver {az,el} (rad)
* int opt I option (0:only offset,1:offset+pcv)
* double *dant O range offsets for each frequency (m)
* return : none
* notes : current version does not support azimuth dependent terms
*-----------------------------------------------------------------------------*/
extern void antmodel(const pcv_t *pcv, const double *del, const double *azel,
int opt, double *dant)
{
double e[3],off[3],cosel=cos(azel[1]);
int i,j;
trace(4,"antmodel: azel=%6.1f %4.1f opt=%d\n",azel[0]*R2D,azel[1]*R2D,opt);
e[0]=sin(azel[0])*cosel;
e[1]=cos(azel[0])*cosel;
e[2]=sin(azel[1]);
for (i=0;ioff[i][j]+del[j];
dant[i]=-dot(off,e,3)+(opt?interpvar(90.0-azel[1]*R2D,pcv->var[i]):0.0);
}
trace(5,"antmodel: dant=%6.3f %6.3f\n",dant[0],dant[1]);
}
/* satellite antenna model ------------------------------------------------------
* compute satellite antenna phase center parameters
* args : pcv_t *pcv I antenna phase center parameters
* double nadir I nadir angle for satellite (rad)
* double *dant O range offsets for each frequency (m)
* return : none
*-----------------------------------------------------------------------------*/
extern void antmodel_s(const pcv_t *pcv, double nadir, double *dant)
{
int i;
trace(4,"antmodel_s: nadir=%6.1f\n",nadir*R2D);
for (i=0;ivar[i]);
}
trace(5,"antmodel_s: dant=%6.3f %6.3f\n",dant[0],dant[1]);
} 以下部分来自网友链接
将地面标志点到平均天线相位中心的向量投影到视线向量e上,将其作为改正值修正到原始的观测值上,不知道这样修正之后得到的距离观测值的实际物理意义是什么,所以接下来的是我个人的理解,不知道是否正确。
个人理解,这种做法是想根据原始ρ得到一个修正到标识上的“假的”观测值P,如下图所示:
其数学关系:
P=RH+SH RH即为代码中的dot(off,e,3),SH=ρ * cosα,由于Mark到APC的距离相比于卫地距很小,可认为SH = ρ,这是因为: ρ-SH=ρ(1-cosα)=x*tan(α/2) ≈ x*sin(α/2)≈x*sinα * 1/2=(x*x)/(2ρ)≈0 所以,P = RH + ρ也就是说,在真观测值ρ上加上改正量RH,即可近似组成假的观测量P,而该观测量是直接联系Mark和Satellite的。
不知道我的理解对不对,因为没看到相关的文献解释这么改正的数学原理,所以暂且认为是这样,等看到相关文献再来修改。
参考:
1、《GPS与北斗卫星多路径效应的对比研究》
2、《GPS测量与数据处理》
3、《GPS多路径效应实例计算与分析》
4、天线高改正和天线相位中心改正
5、GPS从入门到放弃(二十三) --- 相位缠绕