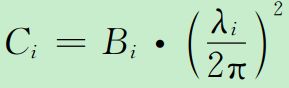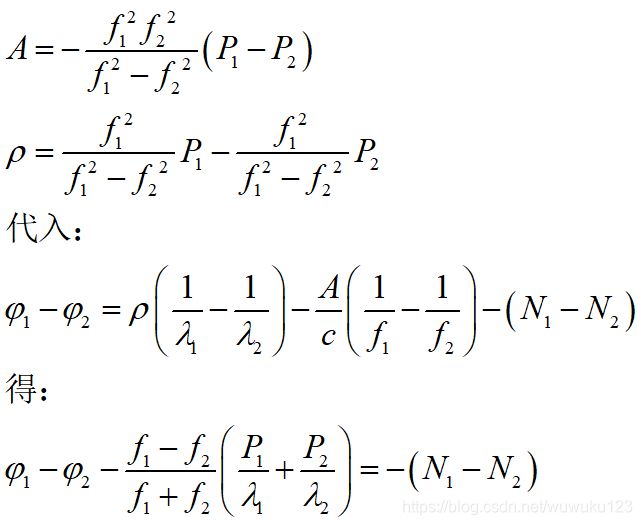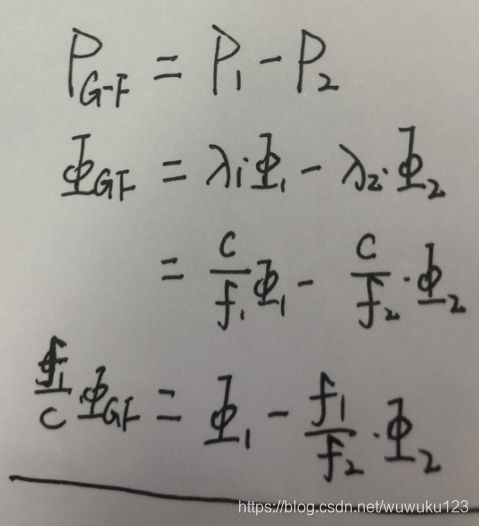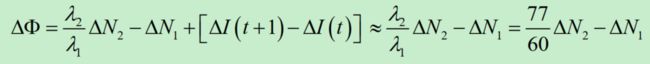GNSS观测值质量分析必备基础知识
一、观测值随机模型
用于描述观测值与未知参数之间关系的模型称为函数模型或数学模型;
而描述观测值本身统计特性的模型称为随机模型,主要通过一个适当的协方差矩阵来定义。
随机模型分类:详见参考3
- 等权随机模型
- 卫星高度角随机模型
- 信噪比随机模型
- 基于验后残差的随机模型
1、等权随机模型 :
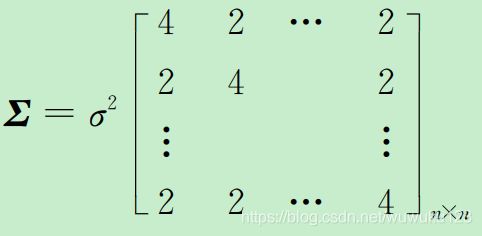
相对定位,认为观测值精度相等,双差中测量噪声,方差-协方差矩阵为:
另外一种表示方式:其中α^2为单差观测值方差,双差观测值的协方差矩阵如下:
2、高度角随机模型:
利用卫星高度角为变量的函数模型对观测量的方差进行估计:
其中Elev为高度角,函数/f通常有指数函数模型、正切函数模型、余弦函数模型、正弦函数模型;一般采用正弦函数模型。
为了更好地定义低高度角观测值地中误差,又常采用改进后地正弦函数模型:
式中,a、b都是经验值,一般取a=3/4mm,b=3mm。
3、载噪比随机模型:
(1)SIGMA-ε 随机模型
Ci的计算为:
式中,Bi为相位跟踪环带宽(Hz);λ为载波相位波长(m)。通常取Cl1=0.00224m^2Hz,Cl2=0.00077m^2Hz。
(2)SIGMA-Δ 随机模型
式中,Δ为模板值与实际观测值之间的差值;α为经验系数,一般取2。
4、信号强度随机模型:
二、GNSS系统观测值质量分析
数据质量是GNSS卫星导航定位的精度和可靠性的重要保障,它受到外业观测环境、接收机自身以及卫星健康状况等诸多因素的影响。如何对GNSS原始观测值的质量作出较为准确的评价,从实测数据中剔除某些质量较差的数据成为高精度GNSS定位首先考虑且首要解决的问题,也是GNSS数据预处理的关键。
数据质量分析指标:详见参考5
- 多路径效应
- 电离层延迟
- 周跳比
- 信噪比
- 数据完整率
- 钟跳
1、伪距多路径效应分析:参考5、6、9
双频伪距、载波相位观测值:
以GPS的L1、L2频点伪距、载波相位为例:
其中,mp1、mp2分别表示L1、L2频点伪距和载波相位观测值的多路径效应组合;P是伪距观测值、λ是频点波长、Φ是载波相位观测值/cycle,α=(f1^2/f2^2);
由于,载波相位中含有未知的模糊度参数/N,因此,上式求的多路径mp1、mp2,包含周跳信息;故在不发生周跳的情况下,可利用多个历元的数据取平均值,再将包含模糊度参数的序列减去该平均值,变得出2个伪距的多路径效应值,可用来衡量多路径效应影响的程度。
其中IGS数据质量检测分析显示,对于多路径效应而言,2/3的IGS站的mp1平均值小于0.5,而2/3的mp2平均值小于0.75。mp1、mp2越小,说明抗多路径效应能立越强。
2、电离层延迟及延迟变化率分析:参考7
3、周跳比分析:参考5
O/slips 是观测值和周跳的比,反映的是数据周跳的情况。
如果某颗卫星再单位历元的两个频率上,检测到周跳情况,则认为该历元产生周跳现象,TEQC软件采用电离层残差法进行周跳的探测与评定,运行的结果文件中以O/slips值来表示观测值与周跳比,O/slips值的参考值为200,O/slips值越小,说明出现周跳越严重。
还有另外一种形式,CSR:
IGS 的数据质量检测分析显示,超过半数的IGS站的CSR平均值小于5,2/3以上的CSR平均值小于10;
4、信噪比/SNR分析:
信噪比,定义为信号功率S与噪声功率N之比,可用来衡量测距信号质量的优劣,信噪比值越大,说明观测信号的质量越好。一般情况下,RINEX文件会直接给出信号的信噪比。
5、数据完整率分析:参考6
数据完整性不仅仅指解析得到的观测历元数占整体应观测到的历元数的比例,还应该反映观测历元内出现的所有卫星的完整观测值,包括P1或者C/A码数据、P2或者C2码数据、L1和L2载波相位数据,W及L1和L2的SNR大于或等于指定的阐值等情况。因此不但要统计缺失历元数,还要在可解析的历元内对观测量的完整性进行统计和标记,并刪除不满足条件的观测数据。对于满足条件的观测数据计数器进行自加,则数据的时间完整性为满足条件的观测数据个数与当前历元和初始历元的差值的比值。
Have(i)为第i颗卫星的完整观测值数目,Expert(i)为第i颗卫星理论观测值数目。
6、钟跳分析:
钟跳与周跳十分类似,都会引起观测数据的跳变,但两者在原理和实质上是不同的,钟跳是接收机钟差的突然变化,可以引起所有卫星伪距或载波相位观测值的同时跳变。
不同的接收机有两种典型的钟跳:
频繁跳跃:在每个历元对接收机时钟进行修正,改正量一般较小,一般情况下可以不考虑;
毫秒跳跃:在接收机钟差达到一定数值时才进行修正。
三、观测值的线性组合
GNSS中,主要利用载波相位、伪距观测值;为了达到某种目的,而进行一系列的变形、组合:
- 同类型同频率观测值的线性组合:
比如:单差、双差等,目的是为了消除一些参数;
- 同类型不同频率观测值的线性组合:
比如:消除电离层延迟,电离层延迟分析
- 不同类型观测值的线性组合:
比如:伪距多路径分析、
1、同类型同频率观测值的线性组合
广为大家熟知的就是 单差、双差;
缺陷/热点:差分观测值间具有了相关性,如何设置随机模型/stochastic model ;对应此博客第一部分;
2、同类型不同频率观测值的线性组合
以GPS L1、L2载波相位为例:
给出线性组合观测值的频率、波长、整周模糊度、电离层延迟、组合观测值测量噪声关系:
或:
一般而言,对于用户有用的组合观测值应该满足以下标准:
- 线性组合后构成的新“观测值”应能保持模糊度的整数特性,以利于正确确定整周模糊度;
- 线性组合后构成的新“观测值”应具有适当的波长;
- 线性组合后构成的新“观测值”应不受或基本不受电离层折射的影响;
- 线性组合后构成的新“观测值”应具有较小的测量噪声;
(1)宽巷组合/Wide Lane
宽巷观测值Φ1-Φ2之差:n=1,m=-1;
利于求解模糊度,噪声为:0.01*sqrt(2)*(0.8619)=1.22厘米
波长为0.86m,模糊度为整数,适于中长基线的模糊度分解。首先用宽巷组合确定双频模糊度之差,然后引入LI组合或L1或L2观测方程,分解出L1模糊度。
(2)无电离层折射延迟组合/ iono-free
具体见:GNSS中多频观测值的组合形式
消电离层组合消除了一阶电离层影响,但模糊度不再为整数了,且观测噪声比L1放大三倍,对中长基线解算有利,可显著改善中长基线解的精度。
(3)窄巷组合
波长为0.107m,模糊度为整数,宽巷组合和窄巷组合中电离层影响的大小相等,符号相反,适用于模糊度分解。
3、不同类型观测值的线性组合
用到了伪距和载波相位;
(1)不同类型的双频观测值间的线性组合之Melboune-Wubbena组合
Melboune-Wubbena组合 (双频伪距和相位组合),推导如下:
消除了电离层延迟、接收机钟差、卫星钟差、卫星至接收机的几何距离;仅受多路径和观测噪声的影响;
其中,ρ为卫星至接收机的距离与所有与频率无关的偏差改正项之和。
推导过程如下:
联合<2><3>代入<1>中,得到:
或:
(2)不同类型的双频观测值间的线性组合之电离层残差组合
在推导Melboune-Wubbena组合中,载波相位Φ1和Φ2单位为:周/cycle;将其乘以波长,得到米/m为单位,进行推导,得到电离层残差组合:
消除了电离层延迟、接收机钟差、卫星钟差、卫星至接收机的几何距离;仅受多路径和观测噪声的影响;
因此,Melboune-Wubbena 和 电离层残差组合,均可以进行模糊度分解和周跳探测;但是周跳探测时,不能对L1、L2频点同时发生的周跳进行检测。
(3)不同类型的单频观测值间的线性组合
由于伪距和载波观测值中电离层延迟大小相同,符号相反,故利用单频伪距P1与载波相位Φ1也能消除电离层延迟:
伪距和相位这种线性组合消除了一阶电离层影响,这种观测量除包含非色散性误差外,还包含一个模糊度参数,比较适用于单点定位,有利于改善定位的精度。
(4)附加:•Geometry-free又称电离层残差组合
这一组合与接收机至卫星的几何距离无关,消除了诸如轨道误差、接收机钟差、卫星误差和对流层误差,仅包含电离层及双频模糊度实数组合,适于电离层研究、数据编辑及周跳探测。
四、周跳探测 需要根据误差传播率计算误差
每颗卫星的观测值在其可视的连续时间内应该是一条光滑的曲线,可通过观测值的线性组合构造合适的周跳检测量,通过求得周跳检测量的时间序列,采用合适的误差判别方法,判断出周跳发生的位置和大小,因此周跳探测与修复的思路如下:
- 利用观测值的线性组合构造合适的周跳检测量;
- 选择合适的误差判别方法;
- 探测周跳检测量序列中突变的位置,判断出是粗差还是周跳;
- 选用合适的方法进行周跳大小的修复;
周跳的本质是探测观测序列是否出现突变!
方法主要有:高次差法、多普勒观测值法、多项式拟合法、M-W组合法、电离层残差法等;
1、高次差法: 参考13,P37
对载波相位观测值,进行相邻历元间做差;
一次差:即卫星至接收机距离变化/速度:
二次差:速度变化/加速度;
三次差:加速度变化/加加速度;
连续跟踪的载波相位值,随着次差的增加,结果趋于0。
其中三次差公式为:
需要注意的是:接收机晶振的短期稳定度、采样率;以此判定用高次差法是否合适。
2、多普勒观测值法
利用历元间载波相位差值 - 多普勒在时间段内积分值;
缺点:易受采样率、接收机钟差、电离层、噪声的影响,只能检测周跳比较大的情况;
3、M-W组合法 / 宽巷相位减窄巷伪距组合
宽巷模糊度
宽巷观测值的整周模糊度主要受伪距多路径和噪声影响,可通过多个历元的平滑进行削弱;
当有周跳发生时,宽巷模糊度为ΔNw=(N1+n1)- (N2+n2),n1、n2为L1、L2载波上的周跳,其值将会出现较大的变化,在实际应用中,联合利用Nw及其均值对周跳的存在性进行判断。利用递推的方法计算出第i个历元的宽巷模糊度均值和方差为:
缺点:1、无法确定周跳发生在哪一个载波上;2、当两个载波上发生周跳大小相同时,将无法探测;
4、电离层残差法 参考14
同一历元双频载波相位测量差:
消除了接收机至卫星间的几何距离、接收机和卫星的钟差、对流层延迟、及部分电离层延迟;剩余误差为:频率间模糊度、电离层影响、多路径效应和观测噪声;
将上式两端同除以λ1,则有:
电离层残差检测方法特点:
- 只用到了双频载波相位观测量,无需其他信息;
- 只能判断出是否出现周跳,不能判断是哪一个频率出现周跳;
如果,电离层延迟变化缓慢,历元间电离层残差相减得到:
其中:77/60=1.28;即如果 |ΔΦ|>0.28,则说明在t+1历元 存在周跳,但是至于在哪一个频率发生周跳,则无法检测出来。
参考:
1、GPS/GLONASS/BDS/Galileo 系统载波相位观测值质量分析
2、北斗与GPS数据质量对比分析
3、基于观测值质量指标的GPS观测量随机模型分析
4、Stochastic Modeling for Static Gps Baseline Data Processing
5、Beidou/GPS/GLONASS多系统卫星定位数据质量比较分析
6、多系统GNSS实时数据质量分析及软件实现 朱静然
7、GNSS观测数据质量分析软件质量设计
8、Assessment of stochastic models for GPS Measurements with different types of receivers
9、GNSS数据质量分析
10、《GPS测量与数据处理》李征航
11、第九讲-观测值的线性组合.ppt
12、GPS观测值的线性组合解析.ppt
13、GNSS观测数据预处理及质量评估
14、基于电离层残差法的周跳探测和修复方法研究