IMU标定+数据融合(一次解决所有困惑内容)
IMU标定+数据融合
1 标定
MEMS惯性器件的误差一般分成两类:系统性误差和随机误差。系统性误差本质就是能找到规律的误差,所以可以实时补偿掉,主要包括常值偏移、比例因子、轴安装误差等。但是随机误差一般指噪声,无法找到合适的关系函数去描述噪声,所以很难处理。一般采用时间序列分析法对零点偏移的数据进行误差建模分析,当然也可以用卡尔曼滤波算法减小随机噪声的影响。
下面会从系统误差、随机误差两个部分去分析IMU组件的标定过程。
1.1 系统性误差
IMU的误差来主要来自于三部分,包括噪声(Bias and Noise)、尺度因子(Scale errors)和轴偏差(Axis misalignments)。加速度计和陀螺仪的测量模型可以用下面来表达。
a B = T a K a ( a S + b a + v a ) w B = T g K g ( w S + b g + v g ) \begin{aligned}&a^{B}=T^{a} K^{a}\left(a^{S}+b^{a}+v^{a}\right)\\&w^{B}=T^{g} K^{g}\left(w^{S}+b^{g}+v^{g}\right)\end{aligned} aB=TaKa(aS+ba+va)wB=TgKg(wS+bg+vg)
其中上标 表示加速度计, 表示陀螺仪,表示正交的参考坐标系, 表示非正交的选准坐标系。表示轴偏差的变换矩阵, 表示尺度因子。
论文A robust and easy to implement method for IMU calibration without external equipments是分析这类误差的经典文献,在博客中有对其方法的具体介绍,不再赘述。具体方法是利用非线性优化的方式,对采集的数据进行数据处理,最终估计出 T T T和 K K K以及 b b b,三个矩阵。再通过上面的计算方式,便得到IMU组件的“真值”。
对于陀螺仪的误差,零偏的处理,会影响到姿态估计的准确性。零偏的算法最好考虑是否静止的状态,再进行校准处理。
这里对陀螺仪的各个参数进行了系统性的介绍。
1.2 ALLAN方差校准随机误差
陀螺仪的随机误差主要包括:量化噪声、角度随机游走、零偏不稳定性、角速率随机游走、速率斜坡和正弦分量。对于这些随机误差,利用常规的分析方法,例如计算样本 均值和方差,并不能揭示出潜在的误差源。另一方面,在实 际工作中通过对自相关函数和功率谱密度函数加以分析将随机误差分离出来是很困难的。
要对陀螺信号进行预处理首先需要对其噪声成分进行辨识。Allan方差分析法是目前最常用的陀螺噪声辨识方法之一。由于Allan方差分析是通过调节Allan方差滤波器带宽,对功率谱进行细致分割,能够辨识出多种不同类型的随机过程误差,并定量分离各项误差系数,而且算法上操作简单、便于计算,在陀螺噪声辨识方面优势明显。
如上所述,在Allan方差分析中,共有5个噪声参数:量化噪声、角度随机游走、零偏不稳定性、速度随机游走和速度爬升。下面主要分析Allan方差的计算、图像的绘制以及最终噪声的分析。
开源项目提供了实例(matlab代码),最终给出下面类似的结果,有参考的价值。
量化噪声 X轴:0.169424 Y轴:0.271556 Z轴:0.581170 单位:arcsec
角度随机游走 X轴:0.225774 Y轴:0.258557 Z轴:0.662383 单位:deg/h^0.5
零偏不稳定性 X轴:0.558054 Y轴:2.620662 Z轴:5.506688 单位:deg/h
角速率游走 X轴:0.511945 Y轴:12.864516 Z轴:54.069972 单位:deg/h/h^0.5
速率斜坡 X轴:5.592172 Y轴:4.763508 Z轴:12.371376 单位:deg/h/h
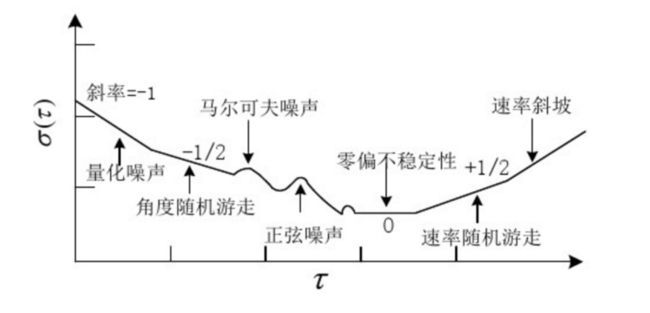
Allan方差实质上就是通过求取整个信息采集过程中相邻时间段的方差形式来对信号在整个时间段内的稳定情况进行衡量的过程。在使用Allan方差分析惯性器件的误差的时候,可以认为惯性器件输出数据的随机部分是由特定的噪声源产生的。在保证测试环境稳定定情况下,可以认为各噪声源是独立的,那么计算出的Allan方差就是各部分误差的平方和。Allan方差的双对数曲线的典型形式以及不同斜率段的曲线代表的噪声成分如下图:
噪声建模如下:
σ t o t a l 2 ( τ ) = σ Q 2 ( τ ) + σ N 2 ( τ ) + σ B 2 ( τ ) + σ K 2 ( τ ) + σ R 2 ( τ ) = 3 Q 2 τ 2 + N 2 τ + 2 B 2 π ln 2 + K 2 τ 3 + R 2 τ 2 2 \begin{aligned}\sigma_{t o t a l}^{2}(\tau) &=\sigma_{Q}^{2}(\tau)+\sigma_{N}^{2}(\tau)+\sigma_{B}^{2}(\tau)+\sigma_{K}^{2}(\tau)+\sigma_{R}^{2}(\tau) \\&=\frac{3 Q^{2}}{\tau^{2}}+\frac{N^{2}}{\tau}+\frac{2 B^{2}}{\pi} \ln 2+\frac{K^{2} \tau}{3}+\frac{R^{2} \tau^{2}}{2}\end{aligned} σtotal2(τ)=σQ2(τ)+σN2(τ)+σB2(τ)+σK2(τ)+σR2(τ)=τ23Q2+τN2+π2B2ln2+3K2τ+2R2τ2
采用allan方差分析陀螺仪的噪声,常常需要将IMU静止放置很久(2小时或者1000s)。可以对上述模型进行简化:
Ω ( t ) = Ω Ideal ( t ) + Bias N ( t ) + Bias B ( t ) + Bias K ( t ) \Omega(t)=\Omega_{\text {Ideal}}(t)+\operatorname{Bias}_{N}(t)+\operatorname{Bias}_{B}(t)+\operatorname{Bias}_{K}(t) Ω(t)=ΩIdeal(t)+BiasN(t)+BiasB(t)+BiasK(t)
使用长时间静止的陀螺仪数据对陀螺仪噪声参数进行分析,上式中,三个噪声参数N(角度随机游走),K(速率随机游走)和B(偏差不稳定性)(或者叫零偏不稳定性)。
结果如下图:
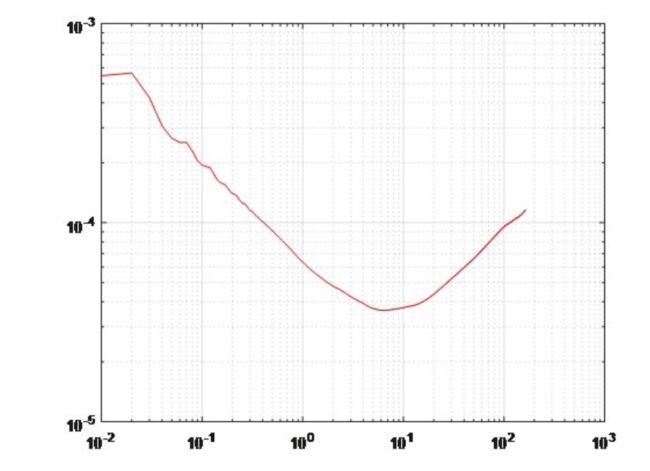
下面举一个例子讨论ALLAN方差的分析过程,采集陀螺仪的数据并做ALLAN分析得到下图。
所以这里的MEMS陀螺所包含的噪声成分主要有:角度随机游走、相关噪声、速率随机游走,而其中代表零偏不稳定性的斜率为0的部分曲线很短,可以认为陀螺中零偏不稳定性影响都相对较小,所以前面进行的陀螺校准得到的零偏可以认为是一个常值。
以上就是通过Allan方差分析得到陀螺仪Bias的过程,一般要采集好几个小时的数据。如果仅需要,零偏参数(bias),则在初始放置的50s左右的时间就足够了。
因此描述一个简单的模型,认为陀螺的数据误差主要是零偏和白噪声:
ω ~ ( t ) = ω ( t ) + b ( t ) + n ( t ) \tilde{\omega}(t)=\omega(t)+b(t)+n(t) ω~(t)=ω(t)+b(t)+n(t)
在得到n(t)之后,就可以设计卡尔曼滤波器进行姿态估计了。
1.3 具体做法
认为是先进行随机误差的标定,然后进行系统误差的标定。有下图:

开源工具介绍
现在已经有成熟的工具包可以使用,imu_utils 可以用来标定随机误差,imu_tk 可以用来标定确定性误差(系统误差),其均是基于LINUX平台下,另外需要安装ROS组件。这里的方法在机器人领域比较常用。
下面是imu_utils的结果,不清楚gyr_w是做什么。
%YAML:1.0
---
type: IMU
name: A3
Gyr:
unit: " rad/s"
avg-axis:
gyr_n: 2.0855329162218030e-03
gyr_w: 3.0516102188797762e-05
x-axis:
gyr_n: 2.1462995497479255e-03
gyr_w: 3.5174142237247770e-05
y-axis:
gyr_n: 2.1439814406437130e-03
gyr_w: 3.2984930038857547e-05
z-axis:
gyr_n: 1.9663177582737710e-03
gyr_w: 2.3389234290287965e-05
Acc:
unit: " m/s^2"
avg-axis:
acc_n: 2.6639085438429400e-02
acc_w: 6.6969300085595741e-04
x-axis:
acc_n: 2.1966919407157028e-02
acc_w: 5.3138962789797575e-04
y-axis:
acc_n: 2.2567628885792314e-02
acc_w: 6.2998018768851071e-04
z-axis:
acc_n: 3.5382708022338866e-02
acc_w: 8.4770918698138565e-04
下面是imu_tk的结果:Given a raw sensor reading X (e.g., the acceleration ), the calibrated “unbiased” reading X’ is obtained.
最终生成两个标定文件,分别为陀螺仪和加速度计的旋转矩阵(misalignment matrix),刻度因数(scale matrix)和零偏(bias)。完成标定,基本格式如下:
Misalignment matrix:
[ 1 -mis_yz mis_zy ]
T = [ mis_xz 1 -mis_zx ]
[ -mis_xy mis_yx 1 ]
Scale matrix:
[ s_x 0 0 ]
K = [ 0 s_y 0 ]
[ 0 0 s_z ]
Bias vector:
[ b_x ]
B = [ b_y ]
[ b_z ]
X' = T*K*(X - B)
2 数据融合
2.1 单位
刚开始接触IMU传感器常常对单位很困惑。我以小觅相机的IMU输出数据举例子。
| 小觅相机 | 其他常用 |
|---|---|
| Acc: g m/s^2(g表示重力加速度) gyro: deg/s |
acc: m/s^2 gyro: rad/s |
2.2 设计滤波器
用滤波器的话有一点要注意:滤波器是会造成延迟的,上篇文章提到过,延迟对控制系统的影响是很大的,所以千万不能为了追求滤波效果,造成大的延迟,通常不要超过一个周期最好。一阶低通效果就足够了,当然也可以设计IIR、FIR之类的。
举个例子,一般飞行器陀螺低通滤波的经验值,带宽是30hz左右,所以就按30hz来计算。
A = T 1 2 π ∗ f c + T A=\frac{T}{\frac{1}{2 \pi * f_{c}}+T} A=2π∗fc1+TT
这里,T表示采样周期,fc表示截止频率,即设置的带宽30hz,这里得到最终的滤波系数为0.2739。
3 比较精彩的一些开源项目
开源:
-
https://github.com/miguelrasteiro/IMU_dataset
-
https://github.com/eruffaldi/imu_comparison_data
这个开源很高级,给出了论文中的图示