IMU相关资料（github上所有有用的开源项目整理）

IMU相关资料

1 标定相关

1.1 资料收集

• 有关于IMU的标定。

• 此外，IMU的标定在github中也有介绍，并且有matlab代码，CSDN。从这个帖子出发，又看到IMU模块的姿态校正，具体代码参看文件。

• matlab仿真，有关于IMU的，不过代码量较大。

• C++代码，编的比较好，可以仿照。已经根据其代码完成了相关的“卡尔曼滤波”的重新设计，并且写完C++代码。

• 从零开始的 IMU 状态模型推导

• matlab仿真比较好，简化了一部分，需要理解他的逻辑是什么，对应博客与csdn，有时间可以看一下他的博客。
  
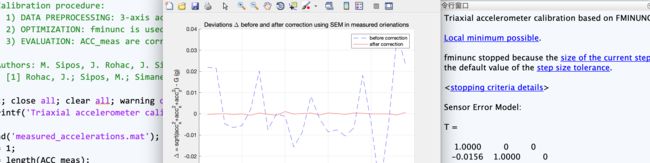
  好像是比较了多种(EKF或者其他滤波的方法)。该作者做了几种标定方式对比的实验，其中有mahony滤波、HLP、EKF等，内容比较完善。

• 另外引用了博客的内容。
  
  此外做了大量IMU与视觉结合的技术，有时间可以看看。
  

• 下图取自代码
  

• 下面博客介绍的比较清楚，有时间阅读一下。
  

• Gait-Tracking-With-x-IMU开源项目，该项目完成了轨迹追踪的标定。在代码中，应该主要采用的是manoy互补滤波器的方法。
  
  
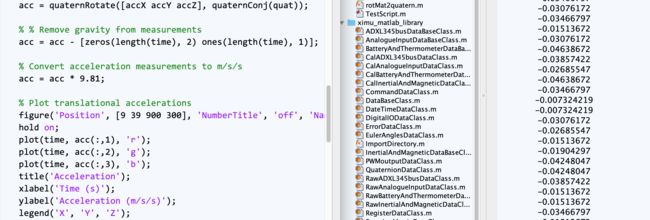
  有必要看一下，貌似设计滤波器进行处理数据了(简单的处理，实际上并没有太多作用)
  

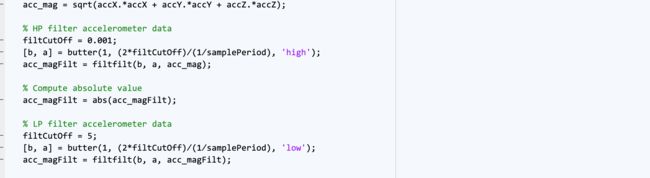
• 基于上面的项目，开启下面的项目。matlab代码写的很清晰。(并且用了上面的数据)
  这里主要的做法是基于上面的数据与对加速度计数据的预处理，进行卡尔曼滤波的设计。卡尔曼滤波的设计主要是基于观测值“v 等于0m/s”的设计。
  
  

• 下面这个博客，有关于IMU的部分，写的比较完整
  
  

• 找到开源项目，代码
  

• 项目，代码
  
  代码很清晰，但是怎么验证其真实性？还有怎么利用这些数据

• 项目，代码
  
  同样是基于“声科技”的代码。
  问题是不能运行，现在需要搞清楚，做标定实验时，需要怎么样的数据？必须要进行有规律的运动？

• 阅读这个人的博客
  《视觉SLAM进阶：从零开始手写VIO》第二讲作业，讲到用工具进行惯组的标定工作(利用utils工具包)
  
  这个人的博客做了很多IMU+视觉SLAM的工作，**有时间可以重点看一下，**参考下面：
  
  我询问小觅相机的技术人员后，直接甩给我文件imu.params:

%YAML:1.0
---
in_accel:
   scale: [ 1., 0., 0., 0., 1., 0., 0., 0., 1. ]
   drift 飘移: [ 0.0, 0.0, 0.0 ]
   noise噪声: [ 0.016925432397973516, 0.016735310195561025, 0.017452487504590969 ]
   bias 偏差: [ 0.00019031356589714596, 0.00016996777864587261, 0.00054490537096493644 ]
in_gyro:
   scale: [ 1., 0., 0., 0., 1., 0., 0., 0., 1. ]
   drift: [ 0., 0., 0. ]
   noise: [ 0.0010848026158819934, 0.0012466367883501759, 0.0011003229919806443 ]
   bias: [ 0.000023404834136742844, 0.000023596771567764949, 0.000014970418056326829 ]
ex_left_to_imu:（）
   rotation: [ -0.0064662, -0.99994994, -0.00763565, 0.99997909, -0.00646566, -0.00009558, 0.0000462, -0.00763611, 0.99997084 ]
   translation: [ 0.00533646, -0.04302922, 0.02303124 ]

1. 陀螺仪的艾伦方差曲线如下：
   
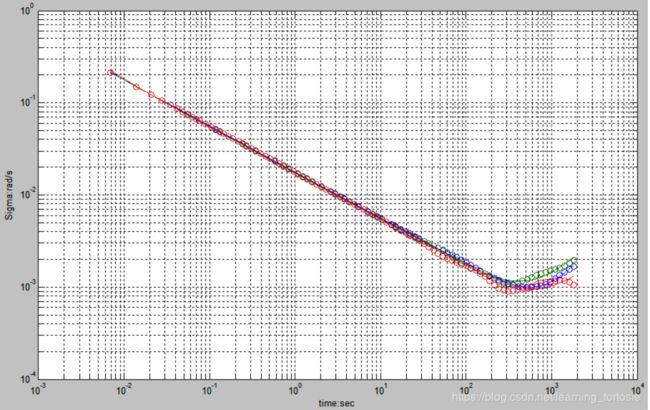
2. 加速度的艾伦方差曲线如下：
   
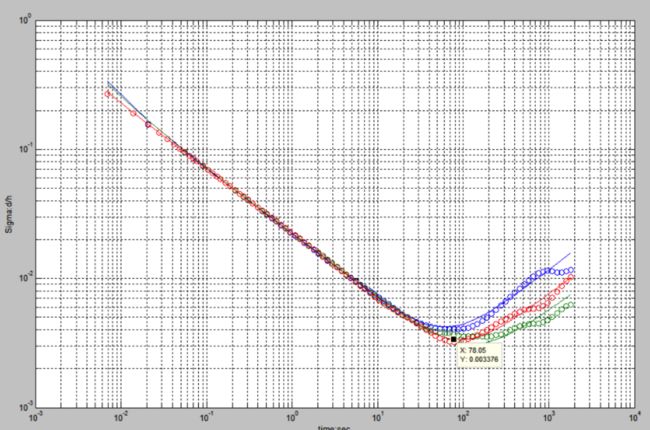
   陀螺仪的高斯白噪声比较准确，但bias随机游走噪声与设定值相差两个数量级，不清楚原因，可能是imu_utlis自身的问题。后面会用kalibr_allan工具标定一下。

1.2 标定工具包

博客采用imu_utils和imu_tk标定imu的确定性误差和随机误差，值得借鉴。

1) imu_utils

• 前面有提到一个工具包，标定IMU的工具包参考港科大的github
  

2) imu_tk

IMU-TK提供简单的函数和数据结构，用于校准基于MEMS的惯性导航单元，以及处理和显示IMU数据。IMU-TK实现了一种多位置校准方法，该方法不需要任何参数调整，只需要手动移动传感器并放置在一组不同的，自动检测的静态位置。IMU-TK还提供了一系列数据集成功能。

• 博客很好的解释了工具包的使用方法与结果。
  • 工具的matlab代码¹和工具包C+代码都是开源的。
    因此可以对比matlab仿真代码与C+的实现代码，在C+中采用的是ceres优化包进行优化，实际上求解的是一个优化问题。
    最终生成两个标定文件，分别为陀螺仪和加速度计的旋转矩阵，刻度因数和零偏。（最终需要的也是这些参数）

引用博客的结果，生成两个标定文件，分别为陀螺仪和加速度计的旋转矩阵，刻度因数和零偏。完成标定。
IMU-TK需要以下工具和库：CMake，Eigen3，Ceres Solver，OpenGL，QT和Gnuplot。要在Ubuntu上安装这些必需的软件包。
安装错误参考²

• 数据的格式是什么？
  目前看没什么特别的。

3) ROS package

• github上这个不错(基于C++)，基于ROS，代码在这里。唯一的问题是手中没有ROS平台。（来自于旷世科技）
  计算IMU方差：通过IMU误差模型，利用程序增加加速度计和陀螺仪的高斯白噪声和bias的噪声，生成静止状态下的IMU数据，然后通过程序计算方差。加速度计和陀螺仪Allan方差曲线如下图所示：
  
  程序中计算得到的是离散时间的噪声，连续时间到离散时间需要除以根号下采样频率。
  总结：从标定结果可以看到，经过转换，加速度计和陀螺仪的高斯白噪声测量值和设定值基本接近，量级在百分之一左右；而加速度计和陀螺仪的bias噪声标定结果与设定结果相差较大，这是由于噪声的量级太小，在万分之一， 所以标定结果会有较大误差；所以这也说明在实际VIO应用中，需要将 IMU的bias加入到后端优化中进行实时估计。
  可以看出，刚开始积分得到的轨迹和实际轨迹很接近，但是很快就飘走了。实际这是很正常的，而且这样的结果已经比较理想，因为仿真产生的IMU数据只考虑了噪声，并没有考虑到地球自转，加速度计与陀螺仪的耦合影响等其它因素的影响；在实际应用中，对于低端IMU进行纯积分，得到的轨迹几秒钟之后立刻就发散了，所以将视觉和IMU，甚至更多传感器融合到一起，取长补短，得到一个鲁棒的SLAM算法是目前研究的热点。

2 仿真部分

2.1 最简单的IMU系统

如果姿态补偿正确，那么利用加速度进行积分，其误差就不是很大了，但是一样会产生漂移，如下图：


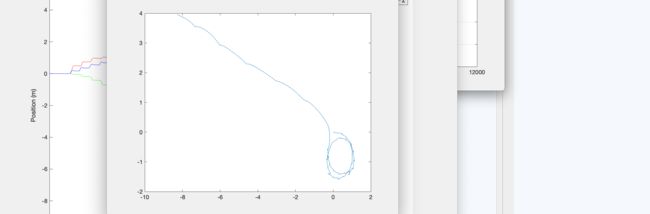
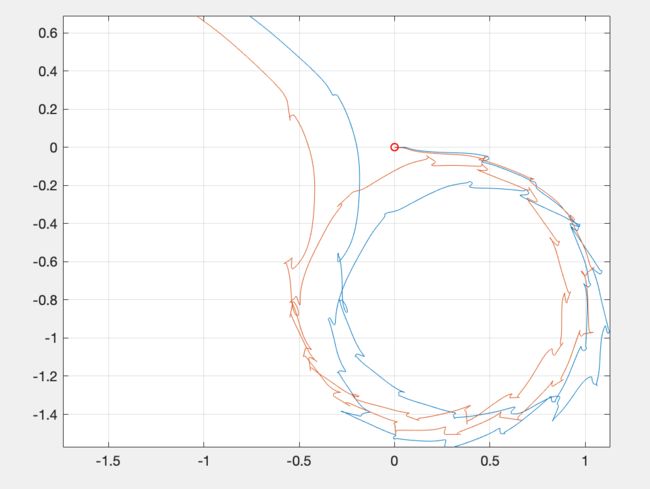
上面可以看到，还是有一定的发散。
但是如何计算一个正确的“角度”呢？仅仅只是一个粗略的计算？下面主要对角度处理，不使用加速度数据补偿角度，那么会有下面做法：(利用四元数与机体角速度之间的关系)

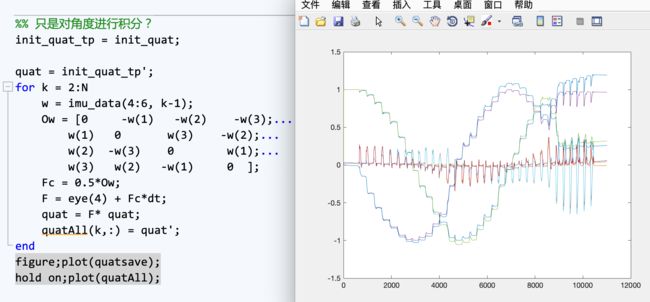
可以看到，即使不采用加速度的数据进行角度的补偿，其结果也是可用的。那么如果直接对惯组角速度进行积分呢？有如下结果，可见，除了存在相位偏差之外，数据还是可以大致使用的。

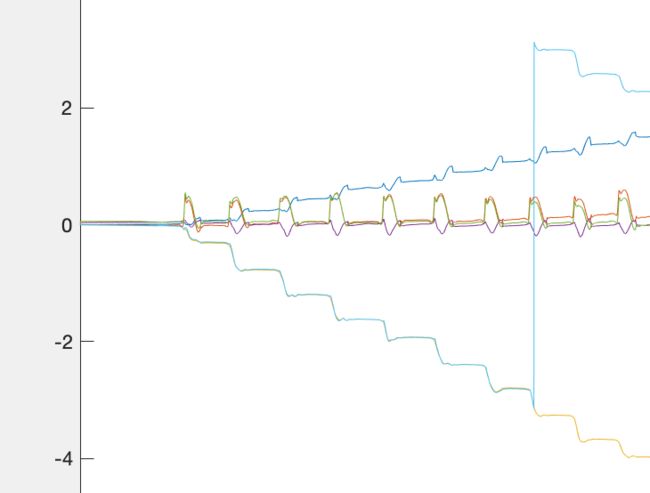
3 原理部分

3.1 惯性系统误差分析

六轴IMU的结构如下图，坐标轴一般遵循右手定则，理想情况下XYZ轴相互正交，加速度计和陀螺仪的轴相互重合。但是通常情况下，IMU存在一定的偏差。例如，从Inven Sense的MPU-9250芯片内部结构图可以看到该加速度计（X、Y、Z轴）和陀螺仪分开制造，因此加速度计和陀螺仪的坐标轴中心并不严格重合，甚至加速度计不同轴也是分开加工，坐标轴也不能保证完全正交。而且，加工过程或多或少有误差，如对称度不好，产生零偏。另外，IMU的内部参数还会随时间、温度变化，产生温漂。

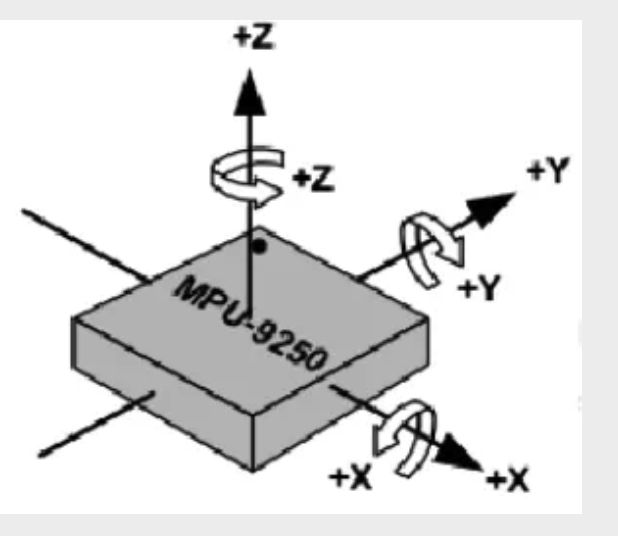
机器人来回运动，当加速度计用于测量重力加速度时，加速度计通常非常嘈杂。陀螺仪的问题在于它会随时间漂移-就像旋转的陀螺仪在失去速度时会开始掉落一样。简而言之，您可以说您只能短期信任陀螺仪，而只能长期信任加速度计。实际上，有一个非常简单的方法可以通过使用一个免费的滤波器来解决这个问题，该滤波器基本上由加速度计上的数字低通滤波器和陀螺仪读数上的数字高通滤波器组成。但是它不如卡尔曼滤波器那么精确，但是其他人已经使用微调的免费滤波器成功构建了平衡机器人。
噪声必须是高斯分布的并且均值为零，幸运的是，对于我们来说，大多数随机噪声都具有此特性。对于系统状态$x_k$来说，系统状态本身是隐藏的，只能通过观察来观察$z_k$。这也称为隐马尔可夫模型。

惯性元件一般指的是加速度计和陀螺仪(有时也包括磁力计)³，它能够感知 3 个正交方向上的线性加速度和旋转角速度。一般地，影响惯性导航性能的主要误 差源包括惯性元件精度和系统误差，例如正交轴的对齐误差、传感器比例因子、 非正交性以及随机噪声等等，将详细的误差源列出如下表格 所示。

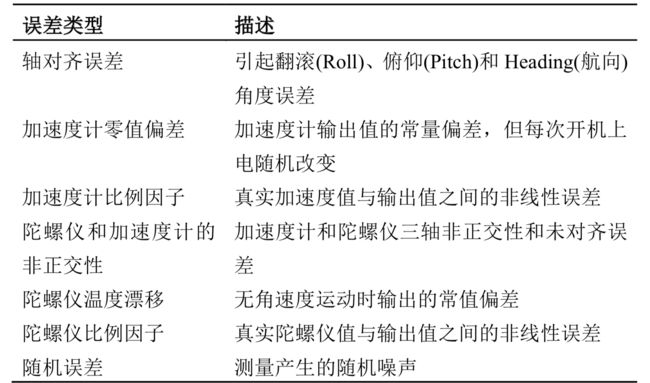
为了评估惯性导航系统的性能，目前存在多种方式，其中易于实现的方法为 将惯性测量单元(Inertial Measurement Unit，IMU)静止一段时间，分析随着时间 增长惯性导航位置漂移量的大小。当然位置估计假设导航误差仅仅由加速度计偏 差引起。实际上位置估计的误差由许多因素造成，包括陀螺仪偏移稳定性、加速度度计比例因子不确定性以及其他因素，但主要的贡献因子是由没有校正的加速度 计偏差引起的。例如在加速度计水平轴上的任何偏差都会导致物体姿态(Roll、 Pitch)估计的误差，姿态矩阵的误差直接关系坐标变换到同一参考系下的加速度 值与实际重力值之差，此偏差(运动加速度)经积分传递到位置误差中，这样加速 度计偏差导致的位置误差将随时间成平方的增长。
因此，惯性元件看似微小的误差对导航输出的干扰不容忽视。学术上，常常 将惯性元件的误差分为两类:确定性误差和随机误差。确定性误差，也叫静态误差，因能被精确建模和表示，可以通过校正或参数标定的方式将其消除。一 般地，在惯性元件使用之前，必须对其校正以消除静态误差影响。

3.2 bias随机游走

为什么bias（固定偏差）会随机游走？

• IMU的bias的随机游走：
  本质上与布朗运动比较像，下面是陀螺仪和加速度计的离散过程：
  $$\hat{\mathbf{a}}[k]=\mathbf{a}[k]+{\mathbf{\sigma }}_a\frac{1}{\sqrt{\Delta t}}\mathbf{w}[k]+{\mathbf{b}}_{dba}[k-1]+{\mathbf{\sigma }}_{ba}\sqrt{\Delta t}\mathbf{w}[k]$$
  $$\hat{\mathbf{g}}[k]=\mathbf{g}[k]+{\mathbf{\sigma }}_g\frac{1}{\sqrt{\Delta t}}\mathbf{w}[k]+{\mathbf{b}}_{dbg}[k-1]+{\mathbf{\sigma }}_{bg}\sqrt{\Delta t}\mathbf{w}[k]$$
  ${\mathbf{b}}_{dbg}[k-1],{\mathbf{b}}_{dba}[k-1]$是上一时刻的bias， ${\mathbf{\sigma }}_{bg}\sqrt{\Delta t}\mathbf{w}[k],{\mathbf{\sigma }}_{ba}\sqrt{\Delta t}\mathbf{w}[k]$ 是上一时刻的随机游走。
  这个博主给出了运动模型与误差模型，值得参考。

3.3 角速度与四元数的关系⁴

角速度与角度之间的关系如下：
$$\dot{\Theta }=W^b\omega$$

$$={\left[\begin{array}{ccc}1& \tan \theta \sin \varphi & \tan \theta \cos \varphi \\ 0& \cos \varphi & -\sin \varphi \\ 0& \sin \varphi /\cos \theta & \cos \varphi /\cos \theta \end{array}\right]}^b\omega$$
有如下关系：
$$\dot{\Theta }=W^b\omega ={\left[\begin{array}{ccc}1& \tan \theta \sin \varphi & \tan \theta \cos \varphi \\ 0& \cos \varphi & -\sin \varphi \\ 0& \sin \varphi /\cos \theta & \cos \varphi /\cos \theta \end{array}\right]}^b\omega$$
旋转矩阵与机体角速度的关系：
$${\dot{R}}_b^e=R_b^e{\left[{}^b\omega \right]}_{\times }$$
四元数与机体角速度之间的关系：
$${\dot{q}}_e^b(t)=\frac{1}{2}\left[\begin{array}{cccc}0& -{\omega }_x& -{\omega }_y& -{\omega }_z\\ {\omega }_x& 0& {\omega }_z& -{\omega }_y\\ {\omega }_y& -{\omega }_z& 0& {\omega }_x\\ {\omega }_z& {\omega }_y& -{\omega }_x& 0\end{array}\right]q_e^b(t)$$
或者寻找三维的（非四元数，只是角速度）的角速度与角度之间的关系，如下面：
旋转矩阵的更新方程为：
$$\begin{array}{rl}\dot{R}(t)& =R(t)\Omega (t)\\ \Omega (t)& =\left[\begin{array}{ccc}0& -{\omega }_{bz}(t)& {\omega }_{by}(t)\\ {\omega }_{bz}(t)& 0& -{\omega }_{bx}(t)\\ -{\omega }_{by}(t)& {\omega }_{bx}(t)& 0\end{array}\right]\end{array}$$
离散化之后：
$$\begin{array}{rl}R(t+\delta t)& =R(t)\cdot \exp \left({\int }_t^{t+\delta t}\Omega (t)dt\right)\\ & =R(t)\left(I+\frac{\sin \sigma }{\sigma }B+\frac{1-\cos \sigma }{{\sigma }^2}{B}^2\right)\end{array}$$
$$\begin{array}{rl}B& ={\int }_t^{t+\delta t}\Omega (t)dt\\ & =\left(\begin{array}{ccc}0& -{\omega }_{bz}(t)\delta t& {\omega }_{by}(t)\delta t\\ {\omega }_{bz}(t)\delta t& 0& -{\omega }_{bx}(t)\delta t\\ -{\omega }_{by}(t)\delta t& {\omega }_{bx}(t)\delta t& 0\end{array}\right)\end{array}$$
取一阶近似：
$$R(t+\delta t)=R(t)(I+B)$$

在代码文件⁵中已经描述的非常清楚。
加速度计的误差通过两次积分带入位置估计，gyro 的误差也同样会带入位置估计。旋转矩阵将 acc 投影到 global 坐标系。姿态的误差将会导致 acc 投影偏差，在垂直方向上无法准确减去 重力加速度 g。

几乎所有 INS 计算中，gyro 的误差都是位置误差的主要来源。因为，大部分应用场景中，重力加速度 g 都远大于运动加速度。

3.4 manhony滤波器

$$\dot{\hat{q}}=\frac{1}{2}\hat{q}\otimes \mathbf{P}(\bar{\Omega }+\delta )$$
$$\delta =k_P\cdot e+k_I\cdot \int e$$
$$e=\bar{v}\times \hat{v}$$


其引用的是无人机开源项目PX4的代码，基于互补滤波器。

---

1. /Users/chenshiming/Downloads/imu_tk_matlab-master ↩︎

2. http://www.mamicode.com/info-detail-2623544.html ↩︎

3. 基于UWBIMU融合的室内定位与导航技术研究.pdf ↩︎

4. https://blog.csdn.net/luoshi006/article/details/51513580 ↩︎

5. zupt.m ↩︎