LeetCode刷题总结(C语言版)_栈队列类
编程总结
每每刷完一道题后,其思想和精妙之处没有地方记录,本篇博客用以记录刷题过程中的遇到的算法和技巧
020)有效括号
给定一个只包括 ‘(’,’)’,’{’,’}’,’[’,’]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串
思路:将字符串都判断如果是左括号(’(’,’[’,’{’,’(’)都进行入栈,遇到其他括号符号则:1)取出栈顶元素,2)同时将栈顶元素的match括号匹配上,3)然后Pop栈顶元素和match元素进行比对,如果一致继续循环判断,否则退出,直到遍历完所有的字符串长度。
typedef char DataType;
typedef struct node{
DataType data;
struct node *next;
} Stack;
Stack* CreateStack(); //创建栈
void StackEmpty(Stack* ); //清空栈
void DestoryStack(Stack*); //撤销(删除)栈
int IsEmpty(Stack*); //判空
int PushStack(Stack*, DataType); //入栈
int PopStack(Stack*); //出栈
DataType GetTopElement(Stack*); //取栈顶元素
#define TRUE_T 1
#define FALSE_T 0
bool isValid(char *s) {
int i = 0;
Stack *stack_tmp;
char c = 0;
char match = 0;
int length = strlen(s);
stack_tmp = CreateStack();
//非成对出现直接return FALSE
if (length % 2 == 1 ) {
return FALSE_T;
}
//“”,输入空字符串,要返回TRUE
if (length == 0 ) {
return TRUE_T;
}
for (i = 0; i < length; i++) {
if (s[i] == '(' || s[i] == '[' || s[i] == '{') {
PushStack(stack_tmp, s[i]);
} else {
if (IsEmpty(stack_tmp)) {
DestoryStack(stack_tmp);
return FALSE_T;
}
//取出栈顶元素
c = GetTopElement(stack_tmp);
PopStack(stack_tmp);
if (s[i] == ')') {
match = '(';
} else if (s[i] == ']') {
match = '[';
} else {
if (s[i] != '}') {
DestoryStack(stack_tmp);
return FALSE_T;
}
match = '{';
}
if (c != match) {
DestoryStack(stack_tmp);
return FALSE_T;
}
}
}
//第一个条件是判断:成对出现"((" ,直接跳过了match判断的操作
//第二个条件是判断栈如果是非空的,栈里面还有符号,也要返回FALSE
if (match == 0 || IsEmpty(stack_tmp) == 0) {
return FALSE_T;
}
DestoryStack(stack_tmp);
return TRUE_T;
}
int main()
{
int n;
char *str = "(()(";
printf("isValid is %d", isValid(str));
return 0;
}
//创建栈,此时栈中没有任何元素
Stack *CreateStack()
{
Stack *stack = (Stack *)malloc(sizeof(Stack));
if (NULL != stack) {
stack->next = NULL;
return stack;
}
return NULL;
}
//清空栈
void StackEmpty(Stack *stack)
{
while (!IsEmpty(stack)) {
PopStack(stack);
}
}
//撤销栈
void DestoryStack(Stack *stack)
{
free(stack);
}
int IsEmpty(Stack *stack)
{
return (stack->next == NULL);
}
//入栈,成功返回1, 失败返回0, 把元素 data 存入栈 stack 中
int PushStack(Stack *stack, DataType data)
{
Stack *newst = (Stack *)malloc(sizeof(Stack));
if (NULL != newst) {
newst->data = data; // 有亚节点的情况
newst->next = stack->next; // 插入到 stack 和 stack->next 之间
stack->next = newst;
return 1;
}
return 0;
}
/*
出栈,成功返回1,失败返回0,出栈不取出元素值,只是删除栈顶元素。
如出栈要实现,取出元素值,并释放空间,可结合取栈顶元素函数做修改,这里不再给出。
*/
int PopStack(Stack *stack)
{
Stack *tmpst;
if (!IsEmpty(stack)) {
tmpst = stack->next; // 有亚节点的情况,Pop stack->next
stack->next = tmpst->next;// stack->next 重新赋予原 stack->next->next 的节点
free(tmpst);
return 1;
}
return 0;
}
//取栈顶元素,仅取出栈顶元素的值,取出之后,该元素,任然存在栈中。成功返回元素值,失败输出提示信息,并返回 -1
DataType GetTopElement(Stack *stack)
{
if (!IsEmpty(stack)) {
return stack->next->data;
}
return -1;
}
C语言实现一个栈往往较为复杂,多数解题是通过一个数组来模拟栈
下面给出用数组模拟上述算法的代码:
bool isTrue(char a, char b)
{
if ((a == '('&&b == ')') || (a == '['&&b == ']') || (a == '{'&&b == '}')) {
return true;
}
return false;
}
bool isValid(const char *s) {
int len = strlen(s);
char str[10000];
int top = -1, i = 0; // top为栈顶
if (len == 0) {
return true;
}
while (i < len)
{
if (top == -1 || !(isTrue(str[top], s[i]))) // 不满足括号匹配
{
top++;
str[top] = s[i]; // 入栈
} else if (isTrue(str[top], s[i])) // 满足括号匹配
{
top--;
}
i++;
}
if (top == -1) { // 最后看栈顶能否回到起始位置
return true;
} else {
return false;
}
}
224)基本计算器
实现一个基本的计算器来计算一个简单的字符串表达式的值。
字符串表达式可以包含左括号 ( ,右括号 ),加号 + ,减号 -,非负整数和空格
一个运算符栈opors,一个运算数栈opands。
括号内的计算优先级最高。
碰到’(‘,’(‘入opors栈。
碰到’)’,opors栈中栈顶到’(‘的运算符都要计算出来。 这表示括号内的表达式结束了,然后, ‘(‘ 出栈。
碰到’+”-‘, opors栈中栈顶到’(‘的运算符都要计算出来。 这是左结合性导致的。然后 ‘+”-‘ 入栈。
碰到数字,提取出整数,然后入opands栈。
#include 队列的典型应用:广度优先遍历
有两种通用的遍历树的策略:
1.深度优先搜索(DFS)
在这个策略中,我们采用深度作为优先级,以便从跟开始一直到达某个确定的叶子,然后再返回根到达另一个分支。
深度优先搜索策略又可以根据根节点、左孩子和右孩子的相对顺序被细分为先序遍历,中序遍历和后序遍历。
2.宽度优先搜索(BFS)
我们按照高度顺序一层一层的访问整棵树,高层次的节点将会比低层次的节点先被访问到。
102)二叉树的层次遍历
给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)。
利用二叉树的,先序遍历,根左右
这里需要注意的是最后是通过二维数组存放结果,对于指针的指针的处理需要注意,并且有树深度(returnSize)返回。
void helper(struct TreeNode* root, int **result, int *ColumnSizes, int i, int *maxh) {
if (root == NULL) { // 递归终止条件
return ;
}
result[i][ColumnSizes[i]] = root->val; // 二叉树的前序遍历
ColumnSizes[i]++; // ColumnSize[i] 存放当前二维数组的列元素
if (i + 1 > *maxh) { // 更新深度,由于 i+1 为深度,传值给 *maxh 为深度
*maxh = i + 1;
}
helper(root->left, result, ColumnSizes, i + 1, maxh); // i + 1 表示层次加1
helper(root->right, result, ColumnSizes, i + 1, maxh); // maxh 表示 树的深度
}
int **levelOrder(struct TreeNode *root, int *returnSize, int **returnColumnSizes) {
int **result = (int **)malloc(sizeof(int *) * MaxSize); // 二维数组,结果存放处, malloc行空间
int i;
for (i = 0; i < MaxSize; i++) { // malloc列空间
result[i] = (int *)malloc(sizeof(int) * MaxSize);
}
*returnColumnSizes = (int *)malloc(MaxSize * sizeof(int));
memset(*returnColumnSizes, 0, MaxSize * sizeof(int));
*returnSize = 0; // 二维数组里行元素个数,也就是树的深度
if (root == NULL) { // 异常判断
return NULL;
}
helper(root, result, *returnColumnSizes, 0, returnSize);
return result;
}
二叉树的层次遍历使用的更多的是利用队列的性质实现BFS,广度优先遍历:
下面还有队列的C语言实现。
#define MAX_QUEUE 10000
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
struct Queue
{
int front; // 队头删除
int rear; // 队尾新增
int size;
struct TreeNode *array[MAX_QUEUE]; // 指针数组
};
void QueueInit(struct Queue *queue)
{
memset(queue, 0, sizeof(*queue));
}
int QueueEmpty(struct Queue *queue)
{
return (queue->size == 0);
}
void QueuePush(struct Queue *queue, struct TreeNode *node)
{
queue->array[queue->rear] = node; // 往队尾增加一个元素
queue->rear++;
printf("Queue Push:queue->rear val %d\n", node->val);
queue->size++;
}
int QueuePop(struct Queue *queue, int *data)
{
if (QueueEmpty(queue)) {
return 0;
}
printf("QueuePop\n");
queue->front = (queue->front + 1);
queue->size--;
return 1;
}
void QueueDestroy(struct Queue* queue)
{
queue->front = 0;
queue->rear = 0;
queue->size = 0;
free(queue->array);
free(queue);
}
struct TreeNode *QueueFront(struct Queue *q)
{
if (q->size == 0)
return NULL;
printf("q->front val %d\n", q->array[q->front]->val);
return q->array[q->front];
}
int **levelOrder(struct TreeNode *root, int *returnSize, int **returnColumnSizes)
{
*returnSize = 0;
*returnColumnSizes = 0;
if (root == NULL) {
return NULL;
}
int layer = 0;
int data = 0;
int **res = (int **)malloc(MAX_QUEUE * sizeof(int *));
struct Queue *q = (struct Queue *)malloc(sizeof(struct Queue));
QueueInit(q);
*returnColumnSizes = (int *)malloc(MAX_QUEUE * sizeof(int));
QueuePush(q, root); // 插入root头结点
while (!QueueEmpty(q)) { // 依次入队头结点/左右节点,然后利用队列性质先进先出队列
int curNum = q->size;
int *array = (int *)malloc(sizeof(int) * curNum);
(*returnColumnSizes)[layer] = curNum; // returnColumnSizes 记录一个数组,数组元素是记录结果每一行的元素个数
printf("--current size curNum-- %d\n", curNum);
for (int i = 0; i < curNum; i++) {
struct TreeNode *node = QueueFront(q); // 获取队头节点
if (node) {
array[i] = node->val; // 获取每一行的结果
printf("-----node->val %d-----\n\n",node->val);
if (node->left) QueuePush(q, node->left); // 左节点入队
if (node->right) QueuePush(q, node->right); // 右节点入队
}
QueuePop(q, &data);// 队头节点出队列
}
res[layer++] = array; // res 是结果存放的二维数组,array是每一行结果存放的一维数组
printf("layer is %d\n", layer); // layer 是记录这个二维数组的行数,即深度
free(array);
}
*returnSize = layer;
free(q);
return res;
}
98)验证二叉搜索树
给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)。
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
bool isValid(struct TreeNode *root, long min ,long max) {
if (root == NULL) {
return 1; // 递归终止条件
}
if (min >= root->val) { //根节点必须大于min
return false;
}
if (max <= root->val) { //根节点必须小于max
return false;
}
return isValid(root->left, min, root->val) && isValid(root->right, root->val, max);
}
bool isValidBST(struct TreeNode *root) {
long min = -2147483649; // 需要注意由于题目的 val 为int型,所以会有用例覆盖到 int的最值(-2147483649 - 2147483647),所以需要将min/max超过这个范围
long max = 2147483649; // 否则,如果出现一个根节点为min,将会直接判断false出去,但一个根节点的结果应该是true
return isValid(root, min, max);
}
- 使用队列实现栈的下列操作:
push(x) – 元素 x 入栈
pop() – 移除栈顶元素
top() – 获取栈顶元素
empty() – 返回栈是否为空
考虑到队列是一种 FIFO 的数据结构,最后入队的元素应该在最后被出队。因此我们需要维护另外一个队列 q2,这个队列用作临时存储 q1 中出队的元素。q2 中最后入队的元素将作为新的栈顶元素。接着将 q1 中最后剩下的元素出队。我们通过把 q1 和 q2 互相交换的方式来避免把 q2 中的元素往 q1 中拷贝
typedef struct SqQueue {
int front;
int rear;
int dataLen;
int data[1024];
} SqQueue_t;
// 初始化队列
SqQueue_t *SqQueueCreate(int dataLen) {
SqQueue_t *queue = (SqQueue_t *)malloc(sizeof(SqQueue_t) + sizeof(int) * dataLen);
queue->front = 0;
queue->rear = 0;
queue->dataLen = dataLen;
return queue;
}
void SqQueueDestroy(SqQueue_t *queue) {
free(queue);
}
int SqQueueFull(SqQueue_t *queue) {
return (queue->front == (queue->rear + 1) % queue->dataLen);
}
int SqQueueEmpty(SqQueue_t *queue) {
return (queue->front == queue->rear);
}
int SqQueuePush(SqQueue_t *queue, int data) {
if (SqQueueFull(queue)){
return -1;
}
// 将数据放置到队尾
queue->data[queue->rear++] = data;
printf("Push:queue->rear is %d, data is %d\n", queue->rear, data);
return 0;
}
int SqQueuePop(SqQueue_t *queue, int *data) {
if (SqQueueEmpty(queue)) {
return -1;
}
// 先进先出,按队头顺序出队列
*data = queue->data[queue->front++];
printf("Pop:queue->front is %d, data is %d\n", queue->front, *data);
return 0;
}
/*---------------------两个队列实现栈---------------------*/
typedef struct {
SqQueue_t *qA;
SqQueue_t *qB;
} MyStack;
/** Initialize your data structure here. */
MyStack *myStackCreate() {
MyStack *stack = (MyStack *)malloc(sizeof(MyStack));
stack->qA = SqQueueCreate(20);
stack->qB = SqQueueCreate(20);
return stack;
}
/** Returns whether the stack is empty. */
bool myStackEmpty(MyStack *obj) {
return (SqQueueEmpty(obj->qA) && SqQueueEmpty(obj->qB));
}
/** Returns whether the stack is empty. */
bool myStackFull(MyStack *obj) {
return (SqQueueFull(obj->qA) || SqQueueFull(obj->qB));
}
/** Push element x onto stack. */
void myStackPush(MyStack *obj, int x) {
if (myStackFull(obj))
return;
SqQueue_t *enQueue = NULL;
if (!SqQueueEmpty(obj->qA)) {
enQueue = obj->qA;
} else {
enQueue = obj->qB;
}
SqQueuePush(enQueue, x);
}
/** Removes the element on top of the stack and returns that element. */
int myStackPop(MyStack *obj) {
if (myStackEmpty(obj)) {
return -1;
}
int data;
SqQueue_t *enQueue = NULL;
SqQueue_t *deQueue = NULL;
SqQueue_t *tmpQueue = NULL;
if (!SqQueueEmpty(obj->qA)) {
deQueue = obj->qA; // qA A队列出数据
enQueue = obj->qB; // qB B队列收数据
} else {
deQueue = obj->qB;
enQueue = obj->qA;
}
while (deQueue->rear != deQueue->front) {
printf("\n");
SqQueuePop(deQueue, &data); // 队列1出数据,队列2收数据
if (!SqQueueEmpty(deQueue)) { // 队列1出完最后一个元素,队列2不接收,直接作为最后一个输出,它就是栈的Top元素
SqQueuePush(enQueue, data);
}
}
printf("rear is %d, front is %d\n", deQueue->rear, deQueue->front);
return data;
}
/** Get the top element. */
int myStackTop(MyStack *obj) {
if (myStackEmpty(obj)) {
return -1;
}
SqQueue_t *enQueue = NULL;
SqQueue_t *deQueue = NULL;
int data;
// 交换deQueue 和 enQueue
if (!SqQueueEmpty(obj->qA)) {
deQueue = obj->qA;
enQueue = obj->qB;
} else {
deQueue = obj->qB;
enQueue = obj->qA;
}
while (deQueue->rear != deQueue->front) {
SqQueuePop(deQueue, &data);
SqQueuePush(enQueue, data);
}
return data;
}
void myStackFree(MyStack *obj) {
SqQueueDestroy(obj->qA);
SqQueueDestroy(obj->qB);
free(obj);
}
int main()
{
MyStack *stack = myStackCreate();
myStackPush(stack, 1);
myStackPush(stack, 2);
myStackPush(stack, 3);
myStackPush(stack, 4);
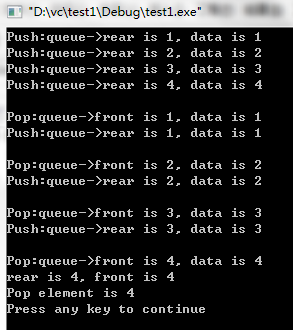
printf("Pop element is %d\n", myStackPop(stack));
return 0;
}
出栈时,队列A会先逐一拷贝元素至另一个队列B,直到最后一个元素Pop出去;
下次出栈时,就反过来,此队列A已经空了,作为存储队列,队列B Push进队列A,直到最后一个元素Pop出去。
typedef struct Stack {
int data[MAX_SIZE];
int top;
int min;
} MinStack; // 为Stack 起了一个别名,后续可以直接使用MinStack来定义变量
MinStack *minStackCreate() {
MinStack *obj = (MinStack *)malloc(sizeof(MinStack));
if (obj) {
obj->top = -1;
obj->min = INT_MAX;
return obj;
}
return NULL;
}
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
pop() —— 删除栈顶的元素。
top() —— 获取栈顶元素。
getMin() —— 检索栈中的最小元素。
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
#include 
