寒假学习笔记【匠心之作，图文并茂】——1.19树的重心、直径、树形 DP

树的重心

还是先看 OI-Wiki 上的定义：

如果在树中选择某个节点并删除，这棵树将分为若干棵子树，统计子树节点数并记录最大值。取遍树上所有节点，使此最大值取到最小的节点被称为整个树的重心。
（这里以及下文中的「子树」若无特殊说明都是指无根树的子树，即包括「向上」的那棵子树，并且不包括整棵树自身。）

看上去挺绕，让我来给你捋捋。

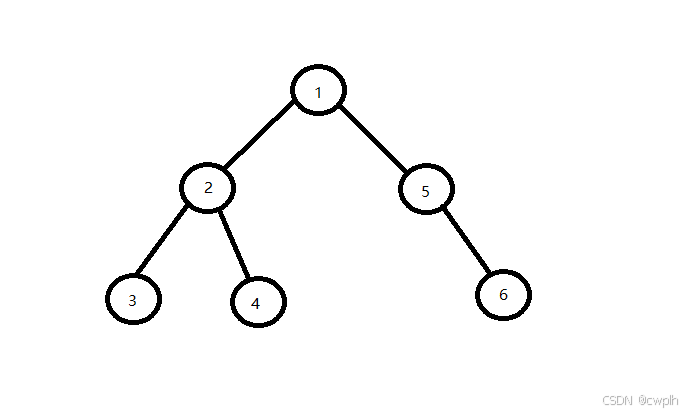
我们先举个例子：

首先我们看去掉 $1$ 号点会发生什么。去掉 $1$ 号点后，整棵树被分成了左右两棵子树，而点数最多的子树的点数则是 $3$。

接着我们看去掉其他点后点数最多的子树的点数是多少。

去掉 $2$ 则是 $3$，去掉 $3,4$ 没影响，去掉 $5$ 为 $4$，去掉 $6$ 没影响。

其中，去掉之后子树点数最少的是 $1,2$：它们的最大子树的点数为 $3$。所以重心就是 $1$ 和 $2$。

现在应该就明白了重心的定义了吧。那具体方法怎么做呢？

很简单，我们只需要用一个 dfs，然后从根节点开始往下搜，然后搜它的子树的大小，再把自身的大小加上它子树的大小表示这棵树总的大小，然后取子树大小中的最大值，最后更新答案。

代码：

#include
#define int long long
using namespace std;
struct edge{
    int ed,nx;
}a[100006];
int n,x,y,cnt,ans=0x3f3f3f3f,vis[100006],head[100006],size[100006],mx[100006];
void add(int st,int ed)
{
    a[++cnt].ed=ed;
    a[cnt].nx=head[st];
    head[st]=cnt;
}
void dfs(int x)
{
    vis[x]=1,size[x]=1;//预处理根节点
    mx[x]=0;
    for(int i=head[x];i;i=a[i].nx)
    {
        if(vis[a[i].ed])//去过就不去了
        {
            continue;
        }
        dfs(a[i].ed);//搜子树
        size[x]+=size[a[i].ed];//加上子树的大小算整棵树的大小
        mx[x]=max(mx[x],size[a[i].ed]);//子树中最大的
    }
    mx[x]=max(mx[x],n-size[x]);//去掉x后两边最大的，看不懂这一步的可以再结合上面那个图自己推一下
    ans=min(ans,mx[x]);//更新
}
signed main()
{
    cin>>n;
    for(int i=1;i<n;i++)//n个点，n-1条边
    {
        cin>>x>>y;
        add(x,y);
        add(y,x);
    }
    dfs(1);
}

树的直径

很简单，先看 OI-Wiki 上的解释：

树上任意两节点之间最长的简单路径即为树的「直径」。

如果看一眼就会写代码的大佬可以先跳过以下内容。

相信大家都能看懂定义，那具体代码怎么实现呢？

这里有一种解法：先从根节点找离它最远的点的编号，然后从那个点开始找直径。

这也很好理解，具体证明大家可以看 这篇文章，我就不在此证明了。

代码挺简单的，留来当课后习题了。

树形 DP

很简单，其实就是在树上做 dp，只要你会一点 dp 的都会写树形 dp。

其中有一点注意事项：树形 dp 需要按照拓扑序（从叶子结点到根节点的顺序）跑。这样才能保证你在叶子结点跑完之后才跑的根节点。一般代码如下：

void dfs(int x)
{
    dp[x]=...;//初始化
    for(int i=head[x];i;i=a[i].nx)//遍历所有子树
    {
        dfs(a[i].ed);//跑到子树
        dp[x]...;//更新状态
    }
}

很简单，看一道版子题。此题来自GoodCoder666的文章：

给定一棵有 $N$ 个结点的树，根结点为结点 $1$。对于 $i=1,2,\dots ,N$ ，求以结点 $i$ 为根的子树大小（即子树上结点的个数，包括根结点）。

这道题十分的简单，只需要把上面的代码稍稍改一下就行。这里我不做解释，具体看代码：

void dfs(int x)
{
    dp[x]=1;//初始化
    for(int i=head[x];i;i=a[i].nx)//遍历所有子树
    {
        dfs(a[i].ed);
        dp[x]+=dp[a[i].ed];//更新状态
    }
}

写个伪代码得了。

换根 DP

这是树形 DP 一个很重要的分支。

换根 DP 主要应用在不知道根节点是哪个的情况下，这时候我们就需要遍历所有的点来依次当根。但这样下去再加上一个 dfs，时间复杂度就直线飙到了 $O(n^2)$，为了降低时间复杂度，我们需要看在换根的这一瞬间发生了什么。

我们以这道例题为例：洛谷 P3478。

题意：让每个点都当一次根，求总的最大深度是多少。

我们这样思考：假设我现在把根转移给了我的子节点，那么被我转移了的那个子节点的总深度就少了 $s_x$（$s_x$ 表示以 $x$ 为根节点往下的总的点数），而其他的子树的总深度就加上了 $n-s_x$。接着我们套上最初的 dp，就得到了一下做法：

假设 $d{p}_x$ 为以 $x$ 为根节点的总深度，即 $d{p}_x=\sum dept{h}_i$，再假设 $y$ 是 $x$ 的子节点，而 $x$ 要将根节点转化给 $y$，则：

$$d{p}_y=d{p}_x-s_y+n-s_y=d{p}_x+n-2\times s_y$$

没理解的可以再多看几遍。

这玩意儿好像也没那么难……

参考文献

OI-Wiki 树的直径

OI-Wiki 树的重心

树形DP算法总结&详解

专题·求树的重心，树的直径【including 例题扫雪系列 I、II