经典IIR数字滤波器设计一般步骤的总结
基于Butterworth模拟LPF进行经典IIR数字滤波器一般设计的步骤总结
趁着这两天刚考完试,DSP忘掉的东西还不多,赶紧写篇note记录一下自己总结的经典IIR数字滤波器的一般设计流程。
说实话,抛开数学上映射关系的原理推导不谈,其实基于巴特沃斯模拟滤波器来设计IIR巴特沃斯数字滤波器的方法和步骤真的是相当简单的。但是老师上课讲课过于注重文字解释和授课模式的线性化,而忽略了用流程图这样简洁清晰的工具,就导致了上课时听的云里雾里,加之学校用的教科书又是相当的不详细且这个学期本身就太短了,短时间吃透是很费力的。我写下这篇文章也是希望之后要学习这门课的同学能够避免我学习时的雷区,假如我当时学的时候有一篇把步骤解读的很清晰的论文或者博客,会节约我很多的时间。还有学DSP一定要用厚书,最好是国外经典教材,在已有优秀经典教材的情况下写薄书教材的行为属于重复造轮子,赚稿费用的。要么是作者从厚书里胡乱抄的,要么就是作者自己对于经典厚书的学习笔记的精炼总结,会有很多文字让人看的不明所以。
废话不多说了,接下来进入正题:
知识点介绍
- 明确应用场景:经典滤波器是指这种滤波器设计方法的特点是信号和干扰的频带互不重叠,在概念上与卡尔曼滤波器、自适应滤波器等现代滤波器相呼应。
- 巴特沃斯(Butterworth)模拟滤波器是一种典型的模拟滤波器,同属此类的还有切比雪夫(Chebyshev)滤波器、贝塞尔(Bessel)滤波器等等
- 所谓“设计”二字,是指给出具体指标后确定传递函数 H a ( s ) H_a(s) Ha(s)或者 H d ( z ) H_d(z) Hd(z)。其中, H a ( s ) H_a(s) Ha(s)与模拟滤波器设计对应, H d ( z ) H_d(z) Hd(z)与数字滤波器设计对应。
- HPF、BSF、BPF、LPF分别对应高通滤波器、带阻滤波器、带通滤波器、低通滤波器。
- IIR与FIR滤波器相对应,前者脉冲响应无限长,后者则为有限长。区别方法就是看差分方程中是否含有“反馈项” y ( n − i ) i = 1 , 2 , 3 , … y(n-i) \quad {i =1,2,3,\ldots} y(n−i)i=1,2,3,…
正文
为了能理解我后面要说的,首先要明确以下几点:
- 设计经典IIR数字滤波器,首先要设计模拟滤波器
- 数字指标要进行归一化,模拟指标也要进行归一化
- 数字域和模拟域本征变量映射的关系由脉冲响应不变法或者双线性变换法确定
假如你之前没有一些滤波器方面的基础(前提是要有DSP基本知识的基础),看到这几点可能还是不知道我在说什么,没关系,下面我会逐点介绍。介绍部分不会很详细,但是我会告诉你为了理解整体步骤,应该去疏通哪一部分知识点。
区别于国内的正常教科书授课思路,我在这里先把如何进行一套完整的设计流程用流程图呈现出来(为了更注重步骤的清晰与简练,以下所涉及的内容都是以经典巴特沃斯IIR数字高通滤波器的设计为例进行,并且不涉及具体的代码实现过程):
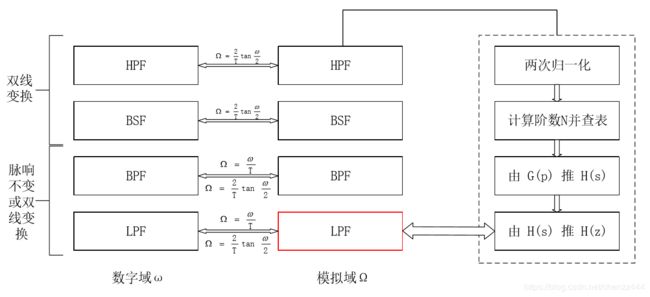
首先我们的目的要十分明确:设计数字滤波器时我们有什么需求?这就对应着率先要给出期望设计或者说期望逼近的数字指标(以数字高通滤波器的设计为例): ω s 、 ω p 、 α s 、 α p \omega_s、\omega_p、\alpha_s、 \alpha_p ωs、ωp、αs、αp,前两个指标往往介于0~2 π \pi π之间,后两个则以单位分贝(dB)给出。(注:角标’s’为“stop”截止的缩写,角标‘p’为“pass”通带的缩写)
步骤1
有了这四个指标后,第二步就要用到我上面说的第一点了,直接把这4个指标转化为相应的模拟域的4个指标: Ω s 、 Ω p 、 α s 、 α p \Omega_s、\Omega_p、\alpha_s、 \alpha_p Ωs、Ωp、αs、αp。
Ω s = 2 T t a n ω s 2 (1.1) \Omega_s = \frac{2}{T} tan \frac{\omega_s}{2} \tag{1.1} Ωs=T2tan2ωs(1.1)
Ω p = 2 T t a n ω p 2 (1.2) \Omega_p = \frac{2}{T} tan \frac{\omega_p}{2} \tag{1.2} Ωp=T2tan2ωp(1.2)
α s = α s (1.3) \alpha_s = \alpha_s \tag{1.3} αs=αs(1.3)
α p = α p (1.4) \alpha_p = \alpha_p \tag{1.4} αp=αp(1.4)
(1.1) 和 (1.2) 就是所谓的双线性变换法中的一个步骤,即指标的预畸变
(1.3) 和 (1.4) 说明通带衰减 α p \alpha_p αp和阻带衰减 α s \alpha_s αs在数字域和模拟域中仍保持不变。
以下我们进行的操作便可暂时不去理会数字域了,把重点放在模拟域上。
经过上述的变换我们已经有了模拟域的4个高通模拟指标,接下来就需要研究怎样把非低通的模拟指标转变为低通的模拟指标。实现方法自然很简单,但要搞懂为什么要这样做呢?原因在于:经典模拟低通滤波器的设计相当成熟,成熟到给我4个模拟低通指标动动小手查一查老前辈们整理好的小表格就可以直接给你 H a ( s ) H_a(s) Ha(s)或者说 G a ( p ) G_a(p) Ga(p)的函数表达式,这也就是为什么我会说“设计经典IIR数字滤波器,首先要设计模拟滤波器”,我还在流程图里把模拟LPF标红了,就是想表明它是沟通数字设计和标准化模拟设计的桥梁。(注:这里的 G a ( p ) G_a(p) Ga(p)假如暂时不理解没关系,后面我们会说到它是归一化的产物,归一化也是实现标准的变量映射的前提)
好,知道原因了就可以介绍接下来的步骤了:
步骤2
把非归一化的模拟高通指标转化为成归一化的模拟高通指标吧!
η s = Ω s Ω c (2.1) \eta_s = \frac{\Omega_s}{\Omega_c} \tag{2.1} ηs=ΩcΩs(2.1)
η p = Ω p Ω c (2.2) \eta_p = \frac{\Omega_p}{\Omega_c} \tag{2.2} ηp=ΩcΩp(2.2)
α s = α s (2.3) \alpha_s = \alpha_s \tag{2.3} αs=αs(2.3)
α p = α p (2.4) \alpha_p = \alpha_p \tag{2.4} αp=αp(2.4)
对于 (2.1) 和 (2.2) 式,习惯上我们会把归一化之后的非模拟低通的指标用 η s \eta_s ηs和 η p \eta_p ηp表示。
而 (2.3) 和 (2.4) 式则继续说明通带衰减 α s \alpha_s αs和阻带衰减 α p \alpha_p αp在数字域和模拟域中仍保持不变。
步骤3
之后又是一次归一化!是把归一化的模拟高通指标化为归一化的模拟低通指标。
λ s = 1 η s (3.1) \lambda_s = \frac{1}{\eta_s} \tag{3.1} λs=ηs1(3.1)
λ p = 1 η p (3.2) \lambda_p = \frac{1}{\eta_p} \tag{3.2} λp=ηp1(3.2)
α s = α s (3.3) \alpha_s = \alpha_s \tag{3.3} αs=αs(3.3)
α p = α p (3.4) \alpha_p = \alpha_p \tag{3.4} αp=αp(3.4)
(3.1) 和 (3.2) 便是归一化的模拟高通和模拟低通之间的转化公式,习惯上把归一化模拟低通的指标用 λ s \lambda_s λs和 λ p \lambda_p λp表示。对于剩下三个非低通型(BSF、BPF、LPF)化为低通型都有着各自的变换关系对,这里不再赘述,会在后面以补充的形式给出简单的介绍。
步骤4
经过这标准的两步归一化操作后,我们便拥有了查表所需的一切原材料,即已经归一化了的4个模拟低通指标: λ s \lambda_s λs、 λ p \lambda_p λp、 α s \alpha_s αs、 α p \alpha_p αp。那么就有:
λ s p = λ s λ p (4.1) \lambda_{sp} = \frac{\lambda_s}{\lambda_p} \tag{4.1} λsp=λpλs(4.1)
k s p = 1 0 0.1 α s − 1 1 0 0.1 α p − 1 (4.2) k_{sp} = \frac{10^{0.1\alpha_s}-1}{10^{0.1\alpha_p}-1} \tag{4.2} ksp=100.1αp−1100.1αs−1(4.2)
N = l g N s p l g λ s p (4.3) N = \frac{lg \ N_{sp}}{lg \ \lambda_{sp}} \tag{4.3} N=lg λsplg Nsp(4.3)
{ Ω c = Ω p ( 1 0 0.1 α p − 1 ) − 1 2 N o r Ω c = Ω p ( 1 0 0.1 α p − 1 ) − 1 2 N (4.4) \begin{cases} \Omega_c = \Omega_p(10^{0.1\alpha_p}-1)^{-\frac{1}{2N}} \\ \ \ \ \ \ \ or \tag{4.4} \\ \Omega_c = \Omega_p(10^{0.1\alpha_p}-1)^{-\frac{1}{2N}} \end{cases} ⎩⎪⎨⎪⎧Ωc=Ωp(100.1αp−1)−2N1 orΩc=Ωp(100.1αp−1)−2N1(4.4)
(4.1) 式,即巴特沃斯模拟滤波器阶数N的计算公式,把上述的4个归一化模拟LPF的指标全部都用上了。通过(4.3) 和 (4.4) 式,只需要查表便可以确定出模拟低通滤波器的归一化传递函数 G a ( p ) G_a(p) Ga(p),其中 Ω c \Omega_c Ωc是截止频率。(注:小角标‘a’为单词“analog”的缩写,表明该函数是模拟而非数字),传递函数里的变量用p来表示,用以区别没有归一化的传递函数(未归一的用变量s)。 有些表格仍是把归一化函数用变量s来代替的,这并不会影响我们的理解。这里 G a ( p ) G_a(p) Ga(p)的阶数对照表不再给出,详细的表格可以参考任何一本DSP教科书。
步骤5
接下来,由 G a ( p ) G_a(p) Ga(p)可以直接导出非归一化的模拟高通滤波器的 H a ( s ) H_a(s) Ha(s):
H a ( s ) = G a ( p ) ∣ p = Ω c s (5.1) H_a(s)=G_a(p)_{ \ | \ p = \frac{\Omega_c}{s}} \tag{5.1} Ha(s)=Ga(p) ∣ p=sΩc(5.1)
步骤6
激动人心的最后一步终于到了!用双线性变换法或者脉冲响应不变法所确定的s域和z域之间的映射关系一步导出 H d ( z ) H_d(z) Hd(z)。对于HPF高通滤波器或是BSF带阻滤波器而言,就只能使用双线性变换法进行映射转换,限于本文篇幅原因,不再展开讲解:
H d ( z ) = H a ( s ) ∣ s = 2 T 1 − z − 1 1 + z − 1 (6.1) H_d(z)=H_a(s)_{ \ | \ s = \frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}} } \tag{6.1} Hd(z)=Ha(s) ∣ s=T21+z−11−z−1(6.1)
至此,我们已经完成了基于巴特沃斯模拟滤波器的经典IIR数字高通滤波器设计啦!
重要补充
- 对于BSF、BPF而言,在确定了数字指标后,也都是经过这6个步骤便可得出最终的设计函数,唯一不同的是BSF和BPF的数字指标个数比HPF稍稍多了那么几个,在确定 λ s \lambda_s λs时有可能还会涉及几个参数的修正,这里也不再展开。
- 请注意:本文呈现出的步骤仅仅介绍了一种设计数字滤波器的实现方案,另一种实现方案:
利用数字域频率变换的设计过程是:先将模拟低通滤波器采用脉冲响应不变法或者双线性变换法转换成数字低通滤波器,再在数字域利用频率变换将低通滤波器转换成所需类型的数字滤波器(例如数字高通滤波器)。
——《数字信号处理第四版》高西全 丁玉美编著
总结
本文全文并未涉及到matlab编程以及滤波器映射原理上的解释,仅仅是简单的来讲一下为什么要经过那么多步转来转去的映射和归一化的中间步骤。这些步骤呈现在代码上只需短短的几行调用,但是它们都是用matlab进行代码实现背后的思路,千万不要做一个只会copy函数而不知其背后原理的调库侠。另外,本文仅为课程学习的笔记与个人对设计步骤的解读,难免存在疏漏与错误之处,有误之处欢迎留言或私信进行批评指正。
PS:本文仅供学习交流使用,未经本人许可不允许商业转载,个人学习用途的转载请注明原文出处,谢谢!