Q-Learning原理+python代码解析+改进

引言

本文代码部分和部分原理介绍是出自莫烦python 强化学习

Q-Learning介绍

一、分类

Q-Learning
(1)、从有无模型的角度属于无模型学习的一种
(2)、从算法更新的角度分别有基于值函数迭代和基于策略迭代。
          策略迭代与值迭代的区别中对这两种算法的区别分别做了介绍。
          在基于策略迭代中又属于时序差分学习（TD）中的异策略算法，《机器学习》一书中提到的就是这种算法。
          基于值函数迭代的算法是本文所研究的。

二、原理概述

在有模型学习中，agent可以每走一步就可以更新当前的值函数。
在蒙特卡洛学习中，agent在运行完一局游戏以后才可以更新状态-动作值函数。
在时序差分学习中，agent结合了有模型学习和蒙特卡罗学习两者的特点。可以每走一步就可以更新当前的状态-动作值函数。
具体来说：

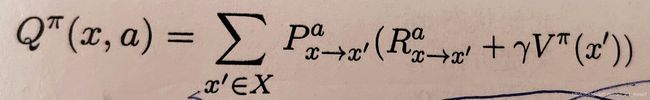
蒙特卡洛算法是将上图中的V全部拆成R贴现加和的形式，经过多次取平均（增量平均形式）
而时序差分学习则是充分利用了马尔科夫结构，通过上图所示的递归形式进行学习，同样也是通过类似增量平均的形式求得期望。
Q-Learning就是时序差分学习（TD）中的异策略算法。所谓异策略指的是在策略迭代算法中，真正更新的策略pai中的动作是使Q（s）取得最大值的动作，而实际选择的动作，是epislion-greedy。但是在值函数迭代过程中，则是尝试下一时间步的时候直接保存Q可以更新的最大值。
策略迭代伪代码：

值迭代伪代码：

三、代码（值迭代）

代码部分是根据莫烦python强化学习章节中写的。训练小圆圈从最左端可以用最少的步数到达最右端，奖励规则是每走一步得到0的奖励，倒数第一个位置如果往右走会得到+1的奖励。

代码讲解

导入工具包

from numpy import random,zeros
from pandas import DataFrame
from time import sleep

名词解释以及定义Q表结构变量

# epsilon#epsilon-greedy
# alpha = 0.1
# gamma = 0.9#the rate of discount,big is to regards feature
# max_episodes#the limit number of episodes
# fresh_time = 0.3#fresh time for one move
state_n = 6#the number of state
actions = ['left','right']#avaiable actions' number

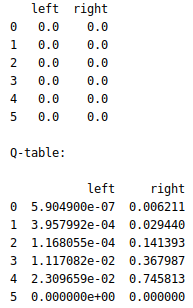
建立Q表，应用在游戏一开始

###new a Q-table value is 0 in start of game###
def build_q_table():
    table = DataFrame(zeros((state_n,len(actions))),columns = actions)#only need to put the value and colums' name to it
    print(table)
    return table

定义选择动作函数（即根据epsilon-greedy选择动作）

###choose action according Q-table and epsilon-greedy
def choose_action(state,q_table,epsilon=0.5):
    state_actions = q_table.iloc[state,:]#acquire the designated row(state)'s action https://www.jianshu.com/p/1115699e0674
    if (random.uniform()>epsilon) or (state_actions.all() == 0):#if 10% probability(to explore) or the designed value is 0(beacuse we can't choice a high reward action)
        action_name = random.choice(actions)#random choice a action
    else:
        action_name = state_actions.idxmax()#choice a high reward action
    return action_name

在选择动作后，定义这一步的奖励以及下一步到达的状态函数：

###give reward according to the current state###
def get_env_feedback(S,A):
    if A == 'right':
        if S == state_n-2:#the final state is 5(because the start is 0)
            S_ = 'terminal'
            R = 1
        else:
            S_ = S + 1
            R = 0
    else:
        R = 0
        if S == 0:
            S_ = S
        else:
            S_ = S - 1
    return S_,R #the new name of S is S_

搭建显示游戏界面函数

###build env(the animation show)###
def update_env(S, episode, step_counter,fresh_time = 0.3):
    env_list = ['-'] * (state_n - 1) + ['T']   #------T the picture
    if S == 'terminal':
        interaction = 'Episode %s:total_step = %s'%(episode + 1, step_counter)
        print('\r{}'.format(interaction),end = '')#only 回车, not 换行
        sleep(2)#if arrive the terminal ,wait 2s
        print('\r                   ',end = '')
    else:
        env_list[S]= 'o'#use 'o' replace '-' in the designed position
        interaction = ''.join(env_list)#because the original env_list is the aggregate of '-' or '0'. the join's function is turn these character into string
        print('\r{}'.format(interaction),end = '')
        sleep(fresh_time)#program suspend there for 0.3s

主程序（基于值迭代，训练结束后返回q表）

###according to de table coding code###
def rl(max_episodes = 13,alpha = 0.1,gamma = 0.9,epsilon=0.9):
    q_table = build_q_table()#new a q-table
    for episode in range(max_episodes):#for all episode
        step_counter = 0
        S = 0#init the agent on the leftest
        is_terminated = False#is not terminate
        update_env(S,episode = episode,step_counter = step_counter)#update show
        while not is_terminated:
            A = choose_action(S, q_table,epsilon=epsilon)#acquire a action
            S_,R = get_env_feedback(S, A)#acquire the reward and the next state
            q_predict = q_table.loc[S, A]#update the designed element(now time-step)
            if S_!= 'terminal':
                q_target = R + gamma*q_table.iloc[S_,:].max()#max element(next time-step)
            else:
                q_target = R
                is_terminated = True
            q_table.loc[S,A] += alpha*(q_target- q_predict)
            S = S_
            update_env(S,episode,step_counter+1)#update show
            step_counter +=1
    return q_table#can see the content of q-table

运行

if __name__ =='__main__':
    q_table = rl()
    print('\r\nQ-table:\n')
    print(q_table)

运行结果

三、改进—epsilon、策略迭代

1、epsilon随游戏进行逐步减小

代码如下

from Q_Learning import update_env,build_q_table,get_env_feedback,choose_action
from numpy import hstack,array
def rl(max_episodes = 13,alpha = 0.1,gamma = 0.9,epsilon=0.6):
    global List
    List = array([0])
    q_table = build_q_table()#new a q-table
    for episode in range(max_episodes):#for all episode
        step_counter = 0
        S = 0#init the agent on the leftest
        is_terminated = False#is not terminate
        epsilon = epsilon+0.06
        if epsilon>1:
            epsilon =1
        update_env(S,episode = episode,step_counter = step_counter)#update show
        while not is_terminated:
            A = choose_action(S, q_table,epsilon=epsilon)#acquire a action
            S_,R = get_env_feedback(S, A)#acquire the reward and the next state
            q_predict = q_table.loc[S, A]#update the designed element(now time-step)
            if S_!= 'terminal':
                q_target = R + gamma*q_table.iloc[S_,:].max()#max element(next time-step)

            else:
                q_target = R
                is_terminated = True
                List = hstack((List,step_counter+1))
            q_table.loc[S,A] += alpha*(q_target- q_predict)
            S = S_
            update_env(S,episode,step_counter+1)#update show
            step_counter +=1
    return q_table#can see the content of q-table
q_table = rl()
print('\r\nQ-table:\n')
print(q_table)
print(List)

为了能够实现公平的对比，采用代码

from numpy import hstack,array,random
random.seed(7)#use the same random number in every episodes

可以运行每次都获得相同序列的随机数。
下面是不同的epsilon的对比，图片显示的是小圆圈从最左边到最右边走的步数。
图一 epslion初始值0.6，每轮增加0.06

图二 epslion初始值0.6，不改变

图三 epslion初始值0.9，不改变

可以看出epsilon=0.6并逐步相信当前决策，与epsilon=0.9差别不大，这是因为环境简单，如果环境复杂，可想而知采用epsilon逐步增加的方法更加适合。但是这两种都比epsilon=0.6好。

2、改为策略迭代

根据策略迭代的算法，首先根据epsilon-greedy选择动作，然后得到奖励和下一步的状态。再根据贪婪策略（选择策略中最大的动作），选择下一动作（值函数迭代中是选择能使当前q值最大的动作，其实两种方法的本质是一样的）。

from Q_Learning import update_env,build_q_table,get_env_feedback
from numpy import hstack,array,random
random.seed(7)#use the same random number in every episodes
###choose action according Q-table and epsilon-greedy
actions = ['left','right']#avaiable actions' number
def choose_action(state,q_table,epsilon=0.5):
    state_actions = q_table.iloc[state,:]#acquire the designated row(state)'s action https://www.jianshu.com/p/1115699e0674
    if (random.uniform()>epsilon) or (state_actions.all() == 0):#if 10% probability(to explore) or the designed value is 0(beacuse we can't choice a high reward action)
        action_name = random.choice(actions)#random choice a action
    else:
        action_name = state_actions.idxmax()#choice a high reward action
    return action_name
def rl(max_episodes = 13,alpha = 0.1,gamma = 0.9,epsilon=0.9):
    global List
    List = array([0])
    q_table = build_q_table()#new a q-table
    for episode in range(max_episodes):#for all episode
        step_counter = 0
        S = 0#init the agent on the leftest
        is_terminated = False#is not terminate
        update_env(S,episode = episode,step_counter = step_counter)#update show
        while not is_terminated:
            A = choose_action(S, q_table,epsilon=epsilon)#acquire a action
            S_,R = get_env_feedback(S, A)#acquire the reward and the next state
            q_predict = q_table.loc[S, A]#update the designed element(now time-step)
            if S_!= 'terminal':
                A_ = q_table.iloc[S_, :].idxmax()  # !!!!!
                q_ = q_table.loc[S_, A_]
                q_target = R + gamma*q_#max element(next time-step)

            else:
                q_target = R
                is_terminated = True
                List = hstack((List,step_counter+1))
            q_table.loc[S,A] += alpha*(q_target- q_predict)
            S = S_
            update_env(S,episode,step_counter+1)#update show
            step_counter +=1
    return q_table#can see the content of q-table
q_table = rl()
print('\r\nQ-table:\n')
print(q_table)
print(List)

四、遇到的问题

1、文件命名

因为本文中用到改进算法，而在编写改进算法的时候调用了之前写的函数，即在另一文件中通过from Q_Learning import 的方式调用源文件编写的函数。
一开始IDE一直不能识别文件名Q-Learning，最后改为Q_Learning的方式命名原文件后正常引用。

2、zeros格式

在定义初始化Q表的时候

    table = DataFrame(zeros((state_n,len(actions))),columns = actions)#only need to put the value and colums' name to it

时，一开始代码为zeros(state_n,len(actions)。
报错：
TypeError: data type not understood。根据博客诡异错误二：TypeError: data type not understood解决。

五、总结与展望

强化学习是当前热门的机器学习分支。本文只是一个传统强化学习的入门，后面还有深度强化学习等更加复杂同时应用场景更广的算法，期待大家共同学习，共同进步！

May the Force be with you.