matlab---s函数讲解之二连杆动力学仿真

matlab虽然后simulink，但是再复杂系统的仿真的时候简单的simulink中模块不能满足要求，因此需要自己建立s函数，作为仿真中的一个模块

在控制系统中分为控制器和被控对象。

零、原理

1、定点控制时，期望为常数，所以可以利用导数为0的特性构造误差动力学，然后构造李雅普诺夫函数，证明稳定性。

一、控制器

1、功能选择函数（flag）

function [sys,x0,str,ts] = spacemodel(t,x,u,flag)
    switch flag
        case 0
            [sys,x0,str,ts] = mdlInitializeSizes;
        case 3
            sys = mdlOutputs(t,x,u);
        case {2,4,9}
            sys = [];
        otherwise
            error(['Unhandlede flag = ',num2str(flag)]);
    end
end

在s函数中，这是必须的一个函数，s函数中的标志为flag有10个，据说目前支持的有0、1、2、3、4、9等几个数值。matlab中S函数的概念及使用

1）flag=0。进行系统的初始化过程，调用mdlInitializeSizes函数，对参数进行初始化设置，比如离散状态个数、连续状态个数、模块输入和输出的路数、模块的采样周期个数、状态变量初始数值等。2）flag=1。进行连续状态变量的更新，调用mdlDerivatives函数。3）flag=2。进行离散状态变量的更新，调用mdlUpdate函数。4）flag=3。求取系统的输出信号，调用mdlOutputs函数。5）flag=4。调用mdlGetTimeOfNextVarHit函数，计算下一仿真时刻，由sys返回。6）flag=9。终止仿真过程，调用mdlTerminate函数。

同时，需要注意对于离散状态更新，每个仿真步内必然调用该子函数，不论是否有意义。Matlab S-function 使用总结

2、初始化函数

function [sys,x0,str,ts] = mdlInitializeSizes
    sizes = simsizes;
    sizes.NumOutputs = 2;
    sizes.NumInputs = 6;
    sizes.DirFeedthrough = 1;
    sizes.NumSampleTimes = 1;
    sys = simsizes(sizes);
    x0 = [];
    str = [];
    ts = [0 0];
end

可以看到在控制器中一般没有状态变量，而状态变量一般都在被控对象中。这也就导致了没有连续状态变量的定义，也就没有了连续状态更新的函数定义（状态方程）。（ps：虽然离散状态更新每个仿真中都会调用，flag=2.）

所以x0不需要定义值，只需要定义空就可以。
ts的值表示每个连续的采样时间步都运行。
sizes.DirFeedthrough = 1：只要输出函数中有u就需要=1。

3、输出函数

function sys = mdlOutputs(t,x,u)
    R1 = u(1);dr1 = 0;
    R2 = u(2);dr2 = 0;

    x(1) = u(3);
    x(2) = u(4);
    x(3) = u(5);
    x(4) = u(6);

    e1 = R1 - x(1);
    e2 = R2 - x(3);
    e = [e1;e2];
    de1 = dr1 - x(2);
    de2 = dr2 - x(4);
    de = [de1;de2];

    Kp = [30 0;0 30];
    Kd = [30 0;0 30];

    tol = Kp*e+Kd*de;

    sys(1) = tol(1);
    sys(2) = tol(2);
end

控制流程图如下：

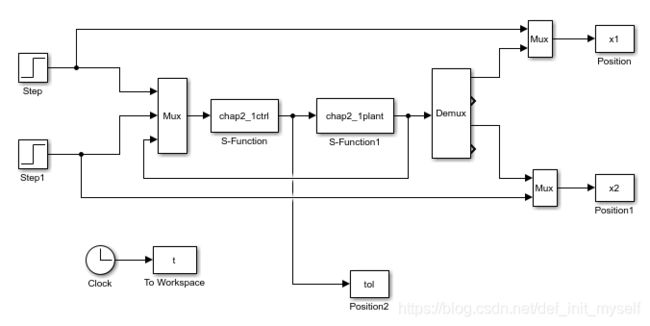
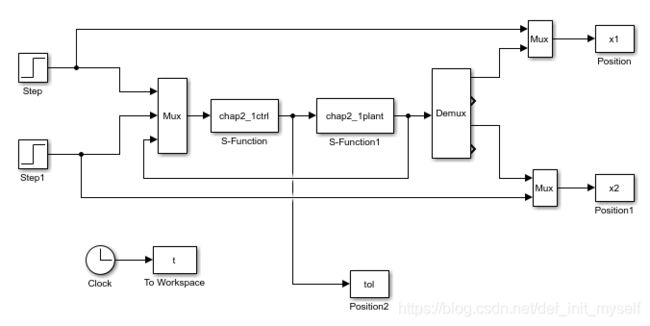
控制器的输入信号之前加了一个Mux，作用是可以将输入向量拼接成一个向量。根据图上的顺序，u1，u2就是输入信号（关节值），u3，u4，u5，u6是那个反馈信号向量中包含的值，也就是被控对象的输出信号。

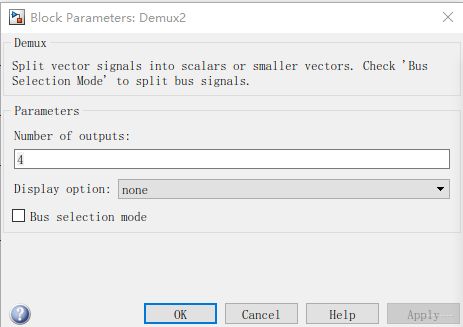
这里关注demux的输出，正如上面所说，被控对象输出4个元素，双击在块设置中如下设置

但是输出连接到mux的只有x1和x3.

u3-u6在后面分析中可以知道，分别是q1，q2以及他们的导数。
然后根据R和q构造e；根据dr和dq构建de，这里因为dr=0，所以设为常数。

二、被控对象

1、功能选择函数（flag）

function [sys,x0,str,ts]=s_function(t,x,u,flag)

switch flag,
%Initialization
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;
case 1,
    sys=mdlDerivatives(t,x,u);
%Outputs
  case 3,
    sys=mdlOutputs(t,x,u);
%Unhandled flags
  case {2, 4, 9 }
    sys = [];
%Unexpected flags
  otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end

因为后面设置了连续状态变量，所以这里需要有状态更新函数设置。

2、初始化函数

function [sys,x0,str,ts]=mdlInitializeSizes
global p g
sizes = simsizes;
sizes.NumContStates  = 4;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 4;
sizes.NumInputs      =2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 0;
sys=simsizes(sizes);
x0=[0 0 0 0];
str=[];
ts=[];

p=[2.9 0.76 0.87 3.04 0.87];
g=9.8;

这里定义的全局变量p在后面的状态更新函数中有用到。
这里因为定义连续状态变量，所以x0不能定义空数组，输入是控制器输出的tol，输出是4个状态变量，虽然最后只连接存储两个。

3、连续状态变量更新函数

function sys=mdlDerivatives(t,x,u)
global p g

D0=[p(1)+p(2)+2*p(3)*cos(x(3)) p(2)+p(3)*cos(x(3));
    p(2)+p(3)*cos(x(3)) p(2)];
C0=[-p(3)*x(4)*sin(x(3)) -p(3)*(x(2)+x(4))*sin(x(3));
     p(3)*x(2)*sin(x(3))  0];
tol=u(1:2);
dq=[x(2);x(4)];

S=inv(D0)*(tol-C0*dq);

sys(1)=x(2);
sys(2)=S(1);
sys(3)=x(4);
sys(4)=S(2);

这里是整个系统中最重要的部分—动力学方程。也就是在这个函数中更新状态变量。这里用到的状态变量有关节角度，以及关节角度的导数。
这里的输出是状态变量的导数，因为这个函数的名称就“求导”。
所以就要先手动求解q的二阶导数。然后和q的一阶导数共同组成“求导的结果。”
目测是当给出导数以后，状态变量的值就会自动更新。

4、输出函数

function sys=mdlOutputs(t,x,u)
sys(1)=x(1);
sys(2)=x(2);
sys(3)=x(3);
sys(4)=x(4);

输出状态变量

三、控制框图

四、代码

1、m

function [sys,x0,str,ts] = spacemodel(t,x,u,flag)

switch flag,
case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;
case 3,
    sys=mdlOutputs(t,x,u);
case {2,4,9}
    sys=[];
otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end

function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumOutputs     = 2;
sizes.NumInputs      = 6;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0  = [];
str = [];
ts  = [0 0];

function sys=mdlOutputs(t,x,u)
R1=u(1);dr1=0;
R2=u(2);dr2=0;

x(1)=u(3);
x(2)=u(4);
x(3)=u(5);
x(4)=u(6);

e1=R1-x(1);
e2=R2-x(3);
e=[e1;e2];

de1=dr1-x(2);
de2=dr2-x(4);
de=[de1;de2];

Kp=[50 0;0 50];
Kd=[50 0;0 50];

tol=Kp*e+Kd*de;

sys(1)=tol(1);
sys(2)=tol(2);

2、m

%S-function for continuous state equation
function [sys,x0,str,ts]=s_function(t,x,u,flag)

switch flag,
%Initialization
  case 0,
    [sys,x0,str,ts]=mdlInitializeSizes;
case 1,
    sys=mdlDerivatives(t,x,u);
%Outputs
  case 3,
    sys=mdlOutputs(t,x,u);
%Unhandled flags
  case {2, 4, 9 }
    sys = [];
%Unexpected flags
  otherwise
    error(['Unhandled flag = ',num2str(flag)]);
end

%mdlInitializeSizes
function [sys,x0,str,ts]=mdlInitializeSizes
global p g
sizes = simsizes;
sizes.NumContStates  = 4;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 4;
sizes.NumInputs      =2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 0;
sys=simsizes(sizes);
x0=[0 0 0 0];
str=[];
ts=[];

p=[2.9 0.76 0.87 3.04 0.87];
g=9.8;
function sys=mdlDerivatives(t,x,u)
global p g

D0=[p(1)+p(2)+2*p(3)*cos(x(3)) p(2)+p(3)*cos(x(3));
    p(2)+p(3)*cos(x(3)) p(2)];
C0=[-p(3)*x(4)*sin(x(3)) -p(3)*(x(2)+x(4))*sin(x(3));
     p(3)*x(2)*sin(x(3))  0];
tol=u(1:2);
dq=[x(2);x(4)];

S=inv(D0)*(tol-C0*dq);

sys(1)=x(2);
sys(2)=S(1);
sys(3)=x(4);
sys(4)=S(2);
function sys=mdlOutputs(t,x,u)
sys(1)=x(1);
sys(2)=x(2);
sys(3)=x(3);
sys(4)=x(4);