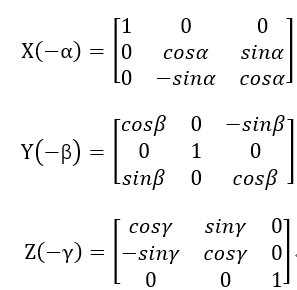ROS-TF学习-欧拉角
前提
在开始本文之前,先做一个定义:
1. 只考虑旋转,不考虑坐标系原点的位移,故世界坐标系与机体坐标系原点是重合的;
2. 世界坐标系 : o-xyz M点在世界坐标系中的坐标 p 坐标向量 [x y z]
3. 机体1坐标系: o-XYZ M点在机体坐标系中的坐标 P 坐标向量 [X Y Z]
欧拉角是Leonhard Euler引入的三个角度来描述刚体相对于固定坐标系的方向或是姿态。欧拉角通常表示为α,β,γ或φ,θ,ψ。
分类
欧拉角大致分为两大类,一类是基于自身坐标系的旋转和,另一类是基于外界坐标系(如世界坐标系)的旋转。
基于自身坐标的旋转
顾名思义,就是绕机体自身的坐标系进行的一系列旋转, 最终得到一个姿态。先绕X还是Y还是Z,这个可以进行选择并组合,所以欧拉角的表示多样。基于自身坐标旋转的组合共有12种,如下:
- 常规欧拉角 (Z-X-Z, X-Y-X, Y-Z-Y, Z-Y-Z, X-Z-X, Y-X-Y)
- 泰特 - 布赖恩角 (X-Y-Z, Y-Z-X, Z-X-Y, X-Z-Y, Z-Y-X, Y-X-Z)
基于外界坐标系的旋转
基于外界坐标系的旋转更为直观的,方便表示。默认外界坐标系是静止的,然后按照其坐标轴进行旋转,组合也同样存在12种。两类方式的旋转在一定条件下,存在等价。
TF功能包中的欧拉角
ROS中的TF功能包中的欧拉角属于泰特 - 布赖恩角,是航模中常用的航向角。
按照自身坐标系旋转顺序是 Z-->Y-->X,叫做eulerYPR(Yaw Pitch Roll);
按照外界坐标系(参考坐标系)的旋转顺序是x-->y-->z,叫做RPY(Roll Pitch Yaw);
描述同一姿态时,以上两者的表示是等价的,即Yaw Pitch Roll的角度值是一样的,这在之后会进行证明。
---------------------
定义:
Yaw 偏航角 ϒ
Pitch 俯仰角 β
Roll 翻滚角 α
----------------------
RPY(Roll Pitch Yaw)
当机体坐标系o-XYZ和参考坐标系o-xyz重合,按照外界坐标系轴(参考坐标系),依次对机体坐标进行旋转,顺序是x(α)-->y(β)-->z(ϒ),取旋转矩阵 x(α) ,y(β),z(ϒ)。
方便理解,采用坐标转换,取点M,其在机体坐标系中坐标为P,当两个坐标重合时,M在外界坐标系中坐标也为P,经过旋转变换,可以得到p,也就是实际点M在外界坐标系中的坐标,表达式如下:
p=z(ϒ)y(β)x(α)P
该式子点M在机体坐标系下的坐标P转换为在外界坐标系下的点p;
z(ϒ)y(β)x(α) 称为外界坐标系到机体坐标系的旋转矩阵 ,也是外界坐标系到机体坐标系的坐标系变换阵;
证明:
[x y z]p=[X Y Z]P
[x y z]R=[X Y Z]
综合,[x y z]p=[x y z]RP 即R=z(ϒ)y(β)x(α)
同理使用坐标转换:
EulerYPR(Yaw Pitch Roll)
有了之前的基础,下面来介绍基于自身坐标系的欧拉角。我们定义旋转顺序是 Z-->Y-->X,角度依次是ϒ 、β、α。
由于是基于自身的旋转,自身的旋转轴相对与外界坐标系是变化的,先前的思路不能使用。
可以这么做,以上旋转等价于将自身坐标系保持不动,外界坐标系依次绕自身坐标系 Z-->Y-->X做-ϒ 、-β、-α角度的旋转。
参照此前的操作,可得等式
P=X(-α)Y(-β)Z(-ϒ)p
发现如下:
由此可得, p=z(ϒ)y(β)x(α)P 和 P=X(-α)Y(-β)Z(-ϒ)p 等价,这里就证明了EulerYPR和RPY等价性。
参考
维基百科——欧拉角
机器人学导论[书]